稳定的算法用于对象排序

稳定的算法用于对象排序

插入与归并等,稳定算法用于对象排序

插入排序

package com.m.algorithm;

import java.util.Arrays;

public class Test {
	/**
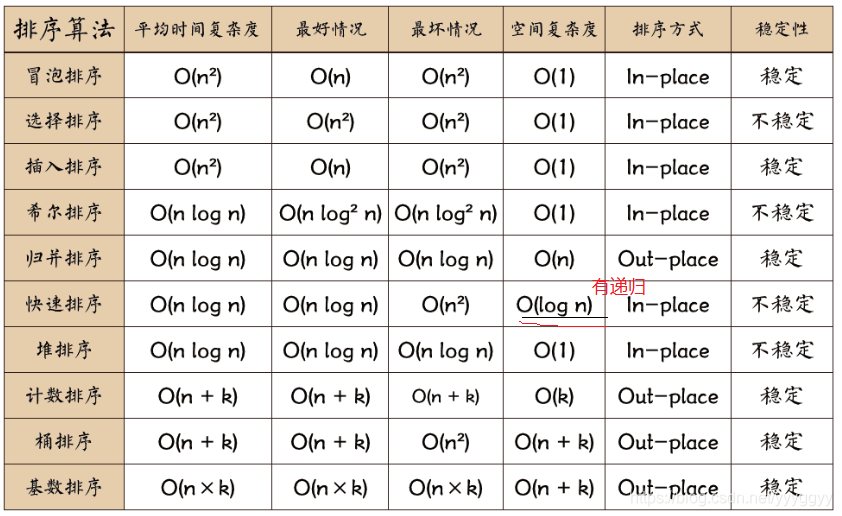
	深入学习排序算法的思路
	
	 * 冒泡 选择
	 * 
	 * 插入(二分) O(n^2) 归并(多路)
	 * 
	 * 希尔 堆排 快排
	 * 
	 * 计数 桶排 基数
	 * 
	 * 
	 * @param args
	 */
	public static void main(String[] args) {
		int[] arr = { 64, 76, 36, 34, 6, 2, 74, 23 };
		long start = System.currentTimeMillis();
		insertSort(arr);
		System.out.println(System.currentTimeMillis()-start);
	}

	public static void insertSort(int[] arr1) {
//		int[] arr1 = { 1, 3, 5, -2 };
		for (int i = 0; i < arr1.length-1; i++) {
			int end = i+1;
			while(end>0 && arr1[end] < arr1[end-1]) {
				int t = arr1[end];
				arr1[end] = arr1[end-1];
				arr1[end-1] = t;
				end--;
			}
		}
		
		System.out.println(Arrays.toString(arr1));
	}
}

归并排序

package com.m.algorithm;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Random;

public class Test {
	
	private List<Integer> arrayTemp;
	
	public Test(List<Integer> arrayTemp) {
		this.arrayTemp = arrayTemp;
	}
	
	public void mergeSort(List<Integer> arrayList,int left,int right) {
		//1、
		if(left < right) {
			int mid = left + (right-left)/2;
			//左分
			mergeSort(arrayList, left, mid);
			//右分
			mergeSort(arrayList, mid+1, right);
			//合并
			merge(arrayList,left,mid,right);
		}
	}
	
	
	public void merge(List<Integer> arrayList,int left,int mid,int right) {
		int index = 0;
		int i = left;
		int j = mid+1;
		
		while(i<=mid && j<=right) {
			if(arrayList.get(i) < arrayList.get(j)) {
				this.arrayTemp.set(index++, arrayList.get(i++));
			}else {
				this.arrayTemp.set(index++, arrayList.get(j++));
			}
		}
		
		while(i<=mid) {
			this.arrayTemp.set(index++, arrayList.get(i++));
		}
		
		while(j<=right) {
			this.arrayTemp.set(index++, arrayList.get(j++));
		}
		
		index = 0;
		while(left <= right) {
			arrayList.set(left++, this.arrayTemp.get(index++));
		}
		
	}
}

插入与归并的JDK的应用

归并的应用-对象排序

Arrays.sort(T[] a, Comparator<? super T> c)的JDK源码 ;

public static <T> void sort(T[] a, Comparator<? super T> c) {
    if (c == null) {
        sort(a);
    } else {
        if (LegacyMergeSort.userRequested)
            legacyMergeSort(a, c);
        else
            TimSort.sort(a, 0, a.length, c, null, 0, 0);
    }
}

/** To be removed in a future release. */
private static <T> void legacyMergeSort(T[] a, Comparator<? super T> c) {
    T[] aux = a.clone();
    if (c==null)
        mergeSort(aux, a, 0, a.length, 0);
    else
        mergeSort(aux, a, 0, a.length, 0, c);
}

TimSort.sort(a, 0, a.length, c, null, 0, 0)的源码

  static <T> void sort(T[] a, int lo, int hi, Comparator<? super T> c,
                         T[] work, int workBase, int workLen) {
        assert c != null && a != null && lo >= 0 && lo <= hi && hi <= a.length;

        int nRemaining  = hi - lo;
        if (nRemaining < 2)
            return;  // Arrays of size 0 and 1 are always sorted

        // If array is small, do a "mini-TimSort" with no merges
        if (nRemaining < MIN_MERGE) {
            int initRunLen = countRunAndMakeAscending(a, lo, hi, c);
            binarySort(a, lo, hi, lo + initRunLen, c);
            return;
        }

        /**
         * March over the array once, left to right, finding natural runs,
         * extending short natural runs to minRun elements, and merging runs
         * to maintain stack invariant.
         */
        TimSort<T> ts = new TimSort<>(a, c, work, workBase, workLen);
        int minRun = minRunLength(nRemaining);
        do {
            // Identify next run
            int runLen = countRunAndMakeAscending(a, lo, hi, c);

            // If run is short, extend to min(minRun, nRemaining)
            if (runLen < minRun) {
                int force = nRemaining <= minRun ? nRemaining : minRun;
                binarySort(a, lo, lo + force, lo + runLen, c);
                runLen = force;
            }

            // Push run onto pending-run stack, and maybe merge
            ts.pushRun(lo, runLen);
            ts.mergeCollapse();

            // Advance to find next run
            lo += runLen;
            nRemaining -= runLen;
        } while (nRemaining != 0);

        // Merge all remaining runs to complete sort
        assert lo == hi;
        ts.mergeForceCollapse();
        assert ts.stackSize == 1;
    }