词法分析（四）：DFA的化简

词法分析概述

---

虽然本篇博客冠名以词法分析，但是DFA的化简对于词法分析来说不是必要的
它仅仅是自动机理论的一部分，甚至，你不需要自动机理论，也可以手打出来一个Tokenizer
但是自动机理论是词法分析器的自动产生工具的理论
自动化并且简化
要不然何以称之为屠龙之术？（虽然前端技术可能只是屠龙术的起式 ）

（词法分析的理论我都看了有一周了，还没着手实现，好tm难 ）

---

DFA的化简（最小化）

DFA的化简（最小化）：对于给定的DFA M，寻找一个状态数比M少的DFA M’，使得L(M)=L(M’)

状态的等价性：
  若 s 和 t 为 M 的两个状态，如果从状态 s 出发可以读出字 α 而停止于终态，
从 t 出发也同样能读出 α 而停止于终态，反之亦然，则称它们是等价的
  两个状态不等价，则称它们是可区分的
（存在一个字可以由状态 s 读出且停止在终态，而不能由状态 t 读出停止在终态，则状态 s 和状态 t 是可区分的）

DFA的化简即是状态集按等价类的划分

• 使任何两个不同的子集中的状态是可区分的，而同一状态中的任意状态间是等价的
• 任何两个子集均不相交
• 最后每个子集保留一个状态

---

DFA的化简过程

由 ε 可以将DFA的状态集区分为 终态 和 非终态 两个子集，形成基本划分Π

假定某个时候，Π包含m个子集，即为Π={I⁽¹⁾，I⁽²⁾，……，I^(m)}，检查Π中的每个子集是否可以进一步划分

检查方法如下：

1. 对某个 I⁽ⁱ⁾，设 I⁽ⁱ⁾ = {s₁，s₂，……，s_n}，
2. 若存在一个输入字符a使得 I_a⁽ⁱ⁾不包含在任何一个现行Π的某个子集 I^(j)中，则 I⁽ⁱ⁾至少应该分为两部分

（若s₁与s₂经过字符a输入后，到达两个不同的状态集，而存在字 α 可以区分这两个状态集，所以字 aα 是可以区分状态s₁与s₂的，即s₁与s₂不等价）

接下来按字符a将 I⁽ⁱ⁾ 分割成分别包含s₁与s₂的两部分 I⁽ⁱ¹⁾ 和 I⁽ⁱ²⁾

• I⁽ⁱ¹⁾含有s₁，I⁽ⁱ¹⁾ = {s|s∈I⁽ⁱ⁾且 s 与 s₁ 经 a弧 到达同一个现行Π的子集}
• I⁽ⁱ²⁾含有s₂，I⁽ⁱ²⁾ = I⁽ⁱ⁾ - I⁽ⁱ¹⁾

分隔出的新子集应添加到检查队列中，判断能否进一步进行划分

一般来说，对某个字符 a 和 子集 I⁽ⁱ⁾，若 I_a⁽ⁱ⁾ 落入现行Π的N个不同子集中，
则应该把 I⁽ⁱ⁾ 按接收字符 a 落入的子集是否相同划分为 N 个不相交的子集

划分完成后，选取每个子集 I 中的一个状态代表该子集，
含有原来初态的子集选出的状态为新的初态，含有原来终态的子集选出的状态为新的终态

---

化简如下DFA

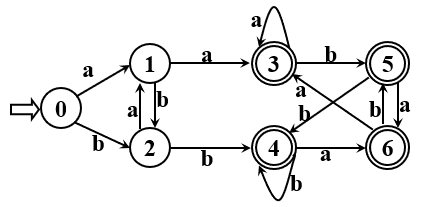
I = {0,1,2,3,4,5,6}，其中终态为{3,4,5,6}

∴初始划分为 I⁽¹⁾ = {3,4,5,6}，I⁽²⁾ = {0,1,2}

等待划分的子集有 I⁽¹⁾、I⁽²⁾，Π = {I⁽¹⁾，I⁽²⁾}

检查 I⁽¹⁾ 是否可以按字符 a 或 b 进行划分，I_a⁽¹⁾包含于 I⁽¹⁾ ，I_b⁽¹⁾也包含于 I⁽¹⁾ ，
即 I⁽¹⁾ 中各状态是等价的，无须划分

等待划分的子集有 I⁽²⁾，Π = {I⁽¹⁾，I⁽²⁾}

检查 I⁽²⁾ 是否可以按字符 a 进行划分，I_a⁽²⁾ = {1,3}，分别落在I⁽¹⁾和I⁽²⁾中，
因此将 I⁽²⁾ 划分为 I⁽²¹⁾ = {0,2}，I⁽²²⁾ = {1}

等待划分的子集有 I⁽²¹⁾、I⁽²²⁾，Π = {I⁽¹⁾，I⁽²¹⁾， I⁽²²⁾}

检查 I⁽²¹⁾ 是否可以按字符 a 划分，（其实已经检查过了 ）， I_a⁽²¹⁾ 包含于 I⁽²²⁾，
检查 I⁽²¹⁾ 是否可以按字符 b 划分，I_b⁽²⁾ = {2,4}，分别落在 I⁽²¹⁾ 和 I⁽¹⁾ 中，
因此将 I⁽²¹⁾ 划分为 I⁽²¹¹⁾ = {0}， I⁽²¹²⁾ = {2}

等待划分的子集有 I⁽²²⁾、I⁽²¹¹⁾、I⁽²¹²⁾，Π = {I⁽¹⁾，I⁽²²⁾，I⁽²¹¹⁾，I⁽²¹²⁾}

I⁽²²⁾大小为1，无须继续划分
I⁽²¹¹⁾大小为1，无须继续划分
I⁽²¹²⁾大小为1，无须继续划分

划分完毕，Π = {I⁽¹⁾，I⁽²²⁾，I⁽²¹¹⁾，I⁽²¹²⁾}
I⁽¹⁾ = {3,4,5,6}，I⁽²²⁾ = {1}，I⁽²¹¹⁾ = {0}，I⁽²¹²⁾ = {2}

则保留状态 0、1、2、3，其中0为初态，3为终态
按照转换关系，得到化简结果如下

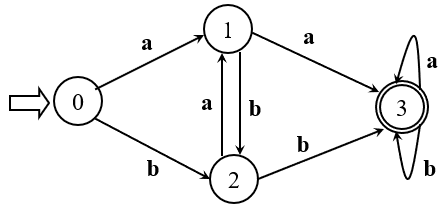
没错，就是酱紫

---

小结

DFA的化简的要点：
  状态的等价和可区分
  最小化算法

---

2019/7/23