形式语言简介
乔姆斯基(Chomsky),美国语言学家,1956年建立形式语言体系,
将文法分为四种类型:0型,1型,2型,3型。称为乔姆斯基谱系
0-型文法(短语文法,图灵机)
产生形式如:α → β
其中:α ∈ (VT∪VN)*且至少含有一个非终结符;β ∈ (VT∪VN)*
1-型文法(上下文有关文法,线性有界自动机)
产生形式如:α → β
其中:|α| ≤|β|,α 长度不大于 β 长度,仅S→ε例外
2-型文法(上下文无关文法,非确定下推自动机)
产生形式如:A →β
其中:A∈VN;β∈(VT∪VN)*
3-型文法(正规文法,有限自动机)
产生式形如:A → αB 或 A → α
其中:α ∈ VT*;A,B ∈ VN(右线性文法)
产生式形如:A → Bα 或 A → α
其中:α ∈ VT*;A,B ∈ VN(左线性文法)
左线性文法与右线性文法的描述能力是等价的
四种类型文法描述能力越来越弱,约束越来越强,越来越具有一般性
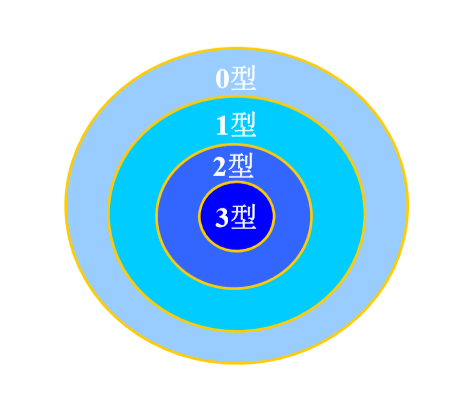
描述能力的包含关系是真包含
例:
L={ anbn|n≥1 }不能由正规文法产生,但可由上下文无关文法产生
G(S): S →aSb | ab
又如

程序设计语言不是上下文无关语言,甚至不是上下文有关语言
如 L={ αcα | α∈{a,b}* }不能由上下文无关文法产生, 甚至连上下文有关文法也不能产生,只能由0型文法产生
L语言中,a,b,c为终结符,α 表示{ a,b }的闭包上的字
在程序设计语言中,常常会出现这种形式的表述,如标识符的引用,形参实参的对应性(个数,顺序,类型),这种要求一致,要求匹配的特点就是 αcα 的语言模式,因此2-型文法无法做到,1-型文法也难以做到
然而现代程序设计语言编译程序仍然使用上下文无关文法描述语言结构。上下文无关文法的分析已经非常成熟高效,并且一个语言大部分的约束都可以使用上下文无关文法实现,因此经过权衡,仍然使用上下文无关文法描述程序设计语言,超出描述能力的部分合并到语义分析中去做
2019/1/26