1、牛顿法
牛顿法是一种在实数域和复数域上近似求解方程的方法。方法使用函数f (x)的泰勒级数的前面几项来寻找方程f (x) = 0的根。牛顿法最大的特点就在于它的收敛速度很快。
具体步骤:
首先,选择一个接近函数 f (x)零点的 x0,计算相应的 f (x0) 和切线斜率f ' (x0)(这里f ' 表示函数 f 的导数)。然后我们计算穿过点(x0, f (x0)) 并且斜率为f '(x0)的直线和 x 轴的交点的x坐标,也就是求如下方程的解:

我们将新求得的点的 x 坐标命名为x1,通常x1会比x0更接近方程f (x) = 0的解。因此我们现在可以利用x1开始下一轮迭代。迭代公式可化简为如下所示:
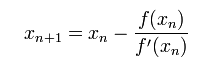
已经证明,如果f ' 是连续的,并且待求的零点x是孤立的,那么在零点x周围存在一个区域,只要初始值x0位于这个邻近区域内,那么牛顿法必定收敛。 并且,如果
f ' (x)不为0, 那么牛顿法将具有平方收敛的性能. 粗略的说,这意味着每迭代一次,牛顿法结果的有效数字将增加一倍。下图为一个牛顿法执行过程的例子。
由于牛顿法是基于当前位置的切线来确定下一次的位置,所以牛顿法又被很形象地称为是"切线法"。牛顿法的搜索路径(二维情况)如下图所示:
牛顿法搜索动态示例图:
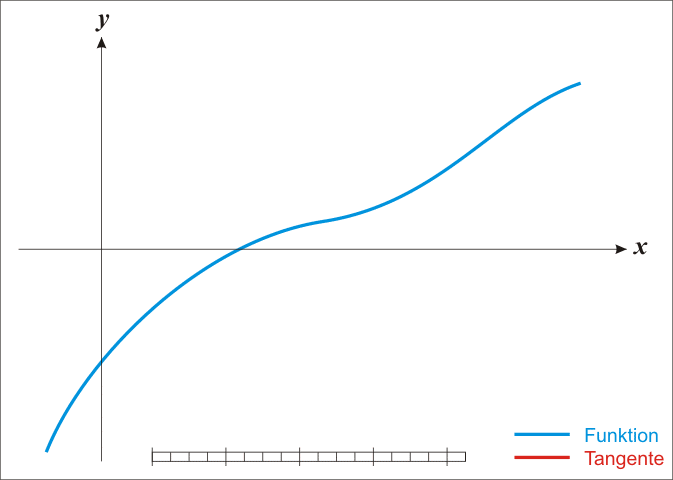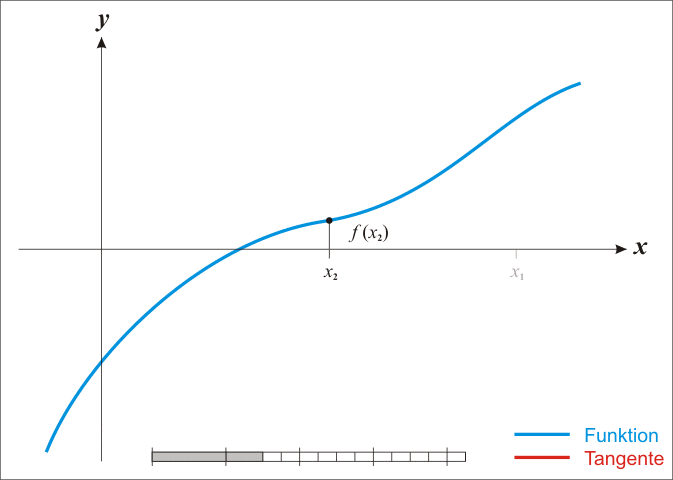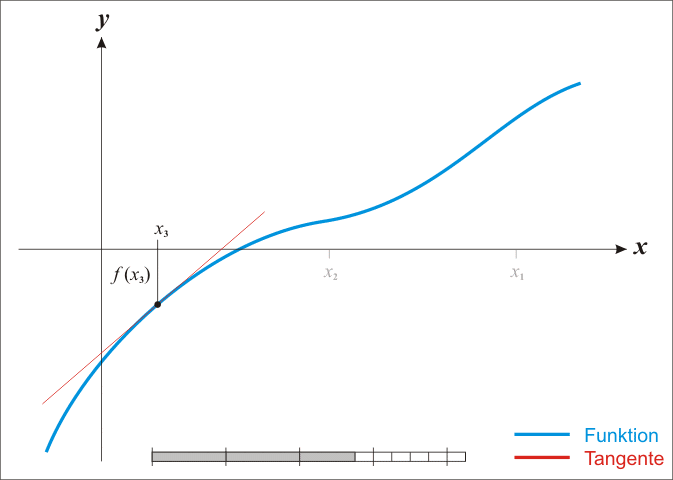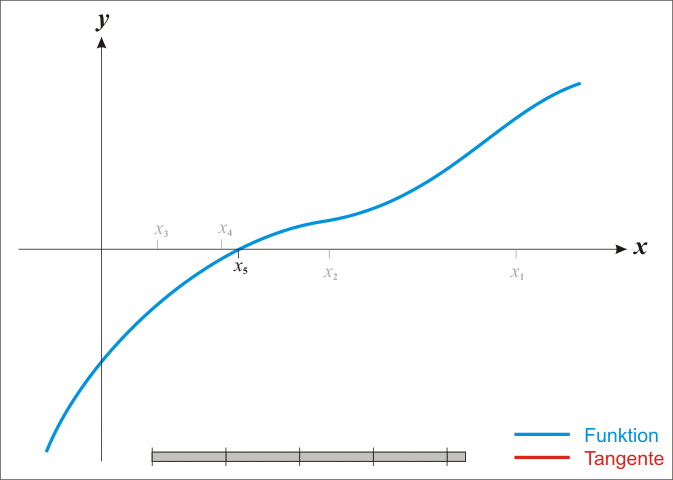
2、拟牛顿法(Quasi-Newton Methods)
拟牛顿法是求解非线性优化问题最有效的方法之一,于20世纪50年代由美国Argonne国家实验室的物理学家W.C.Davidon所提出来。Davidon设计的这种算法在当时看来是非线性优化领域最具创造性的发明之一。不久R. Fletcher和M. J. D. Powell证实了这种新的算法远比其他方法快速和可靠,使得非线性优化这门学科在一夜之间突飞猛进。
拟牛顿法的本质思想是改善牛顿法每次需要求解复杂的Hessian矩阵的逆矩阵的缺陷,它使用正定矩阵来近似Hessian矩阵的逆,从而简化了运算的复杂度。拟牛顿法和最速下降法一样只要求每一步迭代时知道目标函数的梯度。通过测量梯度的变化,构造一个目标函数的模型使之足以产生超线性收敛性。这类方法大大优于最速下降法,尤其对于困难的问题。另外,因为拟牛顿法不需要二阶导数的信息,所以有时比牛顿法更为有效。如今,优化软件中包含了大量的拟牛顿算法用来解决无约束,约束,和大规模的优化问题。
具体步骤:
拟牛顿法的基本思想如下。首先构造目标函数在当前迭代xk的二次模型:





3.1 梯度下降的直观解释
首先来看看梯度下降的一个直观的解释。比如我们在一座大山上的某处位置,由于我们不知道怎么下山,于是决定走一步算一步,也就是在每走到一个位置的时候,求解当前位置的梯度,沿着梯度的负方向,也就是当前最陡峭的位置向下走一步,然后继续求解当前位置梯度,向这一步所在位置沿着最陡峭最易下山的位置走一步。这样一步步的走下去,一直走到觉得我们已经到了山脚。当然这样走下去,有可能我们不能走到山脚,而是到了某一个局部的山峰低处。
从上面的解释可以看出,梯度下降不一定能够找到全局的最优解,有可能是一个局部最优解。当然,如果损失函数是凸函数,梯度下降法得到的解就一定是全局最优解。

3.2 梯度下降的相关概念
在详细了解梯度下降的算法之前,我们先看看相关的一些概念。
1. 步长(Learning rate):步长决定了在梯度下降迭代的过程中,每一步沿梯度负方向前进的长度。用上面下山的例子,步长就是在当前这一步所在位置沿着最陡峭最易下山的位置走的那一步的长度。
2.特征(feature):指的是样本中输入部分,比如2个单特征的样本(x(0),y(0)),(x(1),y(1))(x(0),y(0)),(x(1),y(1)),则第一个样本特征为x(0)x(0),第一个样本输出为y(0)y(0)。
3. 假设函数(hypothesis function):在监督学习中,为了拟合输入样本,而使用的假设函数,记为hθ(x)hθ(x)。比如对于单个特征的m个样本(x(i),y(i))(i=1,2,...m)(x(i),y(i))(i=1,2,...m),可以采用拟合函数如下: hθ(x)=θ0+θ1xhθ(x)=θ0+θ1x。
4. 损失函数(loss function):为了评估模型拟合的好坏,通常用损失函数来度量拟合的程度。损失函数极小化,意味着拟合程度最好,对应的模型参数即为最优参数。在线性回归中,损失函数通常为样本输出和假设函数的差取平方。比如对于m个样本(xi,yi)(i=1,2,...m)(xi,yi)(i=1,2,...m),采用线性回归,损失函数为:
J(θ0,θ1)=∑i=1m(hθ(xi)−yi)2J(θ0,θ1)=∑i=1m(hθ(xi)−yi)2
其中xixi表示第i个样本特征,yiyi表示第i个样本对应的输出,hθ(xi)hθ(xi)为假设函数。
3.3 梯度下降的算法调优
在使用梯度下降时,需要进行调优。哪些地方需要调优呢?
1. 算法的步长选择。在前面的算法描述中,我提到取步长为1,但是实际上取值取决于数据样本,可以多取一些值,从大到小,分别运行算法,看看迭代效果,如果损失函数在变小,说明取值有效,否则要增大步长。前面说了。步长太大,会导致迭代过快,甚至有可能错过最优解。步长太小,迭代速度太慢,很长时间算法都不能结束。所以算法的步长需要多次运行后才能得到一个较为优的值。
2. 算法参数的初始值选择。 初始值不同,获得的最小值也有可能不同,因此梯度下降求得的只是局部最小值;当然如果损失函数是凸函数则一定是最优解。由于有局部最优解的风险,需要多次用不同初始值运行算法,关键损失函数的最小值,选择损失函数最小化的初值。
3.归一化。由于样本不同特征的取值范围不一样,可能导致迭代很慢,为了减少特征取值的影响,可以对特征数据归一化,也就是对于每个特征x,求出它的期望x¯和标准差std(x)。
这样特征的新期望为0,新方差为1,迭代次数可以大大加快。
4. 梯度下降法大家族(BGD,SGD,MBGD)
4.1 批量梯度下降法(Batch Gradient Descent)
批量梯度下降法,是梯度下降法最常用的形式,具体做法也就是在更新参数时使用所有的样本来进行更新。
由于我们有m个样本,这里求梯度的时候就用了所有m个样本的梯度数据。
4.2 随机梯度下降法(Stochastic Gradient Descent)
随机梯度下降法,其实和批量梯度下降法原理类似,区别在与求梯度时没有用所有的m个样本的数据,而是仅仅选取一个样本j来求梯度。对应的更新公式是:
随机梯度下降法,和4.1的批量梯度下降法是两个极端,一个采用所有数据来梯度下降,一个用一个样本来梯度下降。自然各自的优缺点都非常突出。对于训练速度来说,随机梯度下降法由于每次仅仅采用一个样本来迭代,训练速度很快,而批量梯度下降法在样本量很大的时候,训练速度不能让人满意。对于准确度来说,随机梯度下降法用于仅仅用一个样本决定梯度方向,导致解很有可能不是最优。对于收敛速度来说,由于随机梯度下降法一次迭代一个样本,导致迭代方向变化很大,不能很快的收敛到局部最优解。
那么,有没有一个中庸的办法能够结合两种方法的优点呢?有!这就是4.3的小批量梯度下降法。
4.3 小批量梯度下降法(Mini-batch Gradient Descent)
小批量梯度下降法是批量梯度下降法和随机梯度下降法的折衷,也就是对于m个样本,我们采用x个样本来迭代,1<x<m。一般可以取x=10,当然根据样本的数据,可以调整这个x的值。
5. 梯度下降法和其他无约束优化算法的比较
在机器学习中的无约束优化算法,除了梯度下降以外,还有前面提到的最小二乘法,此外还有牛顿法和拟牛顿法。
梯度下降法和最小二乘法相比,梯度下降法需要选择步长,而最小二乘法不需要。梯度下降法是迭代求解,最小二乘法是计算解析解。如果样本量不算很大,且存在解析解,最小二乘法比起梯度下降法要有优势,计算速度很快。但是如果样本量很大,用最小二乘法由于需要求一个超级大的逆矩阵,这时就很难或者很慢才能求解解析解了,使用迭代的梯度下降法比较有优势。
梯度下降法和牛顿法/拟牛顿法相比,两者都是迭代求解,不过梯度下降法是梯度求解,而牛顿法/拟牛顿法是用二阶的海森矩阵的逆矩阵或伪逆矩阵求解。相对而言,使用牛顿法/拟牛顿法收敛更快。但是每次迭代的时间比梯度下降法长。