题目地址
一道可以用贪心做的树形DP题。
对于深度最深的点,要使它被覆盖到,可以在它的兄弟、父亲、爷爷处设立消防局,而在它的爷爷设置消防局最优因为这样可以管到爷爷的爷爷。
每设立一个消防局,又要把它能管到的地方都标记一遍。所以要打两个标记。一个标记记录它是否被任何一个消防局管到过(vis)。一个标记(book)记录它能否被当前设立的这一个消防局管到,这个标记要在设立下一个消防局时清零。
原因:(book)是防止父亲和儿子之间来回搜(加的双向边嘛)。如果遇到一个点的(book)为1,就会(continue),但如果这个(book)是被之前设立的消防局标记的,就会出现错误。
举个例子:
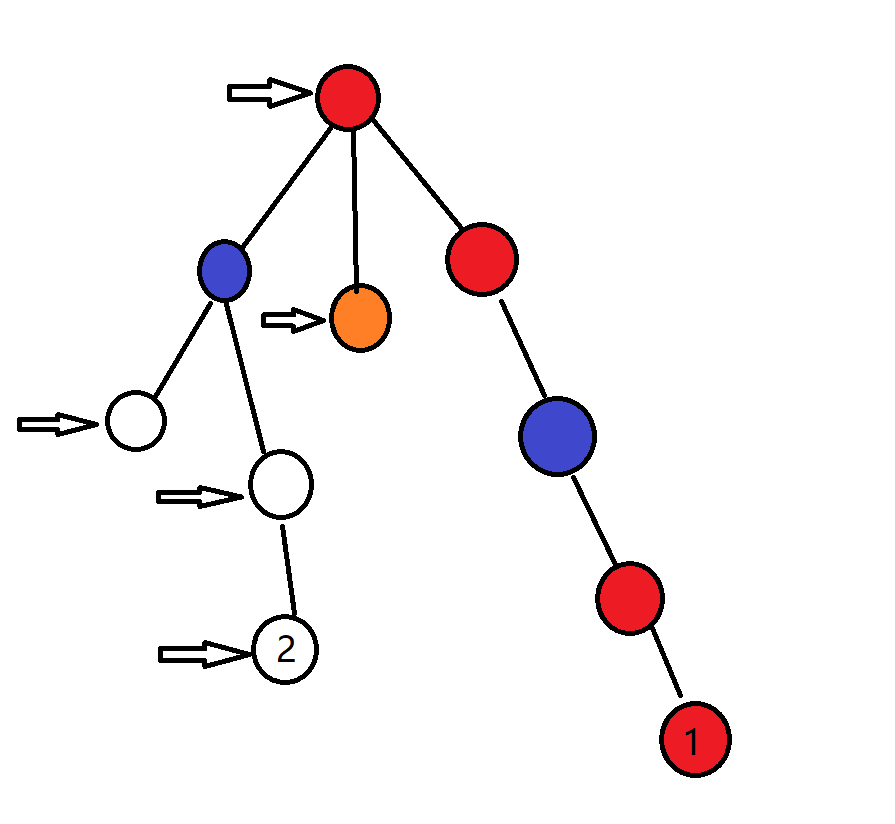
假如第一次取出最深的点1,相当于在右边的蓝色点设立消防局,那么所有红色的点的(book)都被标记过了。如果不清0的话,第二次选到2号点,相当于在左边的蓝色点设立消防局,它应该将所有标箭头的点都标记,但以为上一次标记的(book)没有清空,当搜到最上面的红色的点时,就会返回,所以橙色的点并没有被标记到(它应该被标记)。那么下次又会取出橙色的点。很明显答案错误。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 10005;
int n,head[N],tot,ans;
struct edge{
int next,node;
}e[20005];
struct nod{
int dep,p;
}a[N];
bool vis[N],book[N];
void add(int x,int y)
{
e[++tot].node=y;
e[tot].next =head[x];
head[x]=tot;
}
bool cmp(nod a,nod b)
{
return a.dep >b.dep;
}
void build(int u,int fa)
{
a[u].p=u; a[u].dep=a[fa].dep+1;
for(int i=head[u];i;i=e[i].next)
{
int v=e[i].node;
if(v==fa) continue;
build(v,u);
}
}
void dfs(int u,int sum)
{
book[u]=vis[u]=1;
if(!sum) { book[u]=0; return;}
for(int i=head[u];i;i=e[i].next)
{
int v=e[i].node;
if(book[v]) continue;
dfs(v,sum-1);
}
book[u]=0;
}
/*void dfs(int x,int size)
{
vis[x]=book[x]=1;
for(int i=head[x];i;i=e[i].next)
{
int to=e[i].node;
if(!book[to]&&size>0)
dfs(to,size-1);
}
book[x]=0;
}*/
int main()
{
scanf("%d",&n);
int x;
for(int i=2;i<=n;i++)
{
scanf("%d",&x);
add(i,x); add(x,i);
}
build(1,0);
sort(a+1,a+n+1,cmp);
for(int i=1;i<=n;i++)
if(!vis[a[i].p])
++ans,dfs(a[i].p,4);
printf("%d
",ans);
return 0;
}