树链剖分——轻重链剖分
blog
https://blog.csdn.net/qq_40482358/article/details/89676297
把树上的问题转化成序列问题(然后就快乐线段树维护)
概括一下就是把树划分为若干条链,然后一个链的dfs序是连续的,对于树上两点,我们可以通过跳链直到两者在同一条链上,然后链上的权值就是区间问题
定义:
重儿子:所有儿子中子树(siz)最大的点,其他的都叫轻儿子
重链:所有重儿子穿成的(许多条)链,其他的都叫轻链
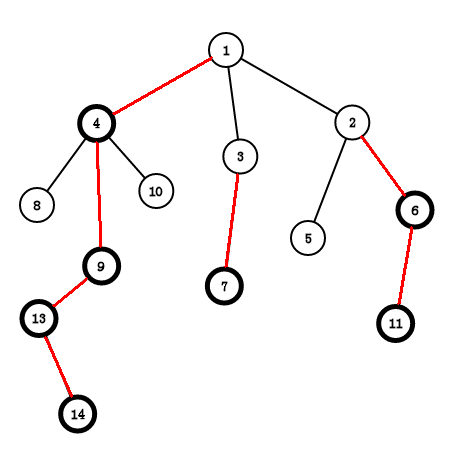
性质:
1.若(u,v)为一条轻边,$ size(v)<size(u)/2$
2.从根节点到任意节点的路径 经过的轻边数量 小于 logn,经过的重边数量 也小于 logn
可以得出,树链剖分的时间复杂度为(O(nlog^2n)) ,是一种优秀的算法。
求出重儿子,深度,子树大小
void dfs_son(int x,int f){
siz[x]=1;fa[x]=f;dep[x]=dep[f]+1;
for(int i=hd[x];i;i=nxt[i]){
int y=to[i];
if(y==f)continue;
dfs_son(y,x);
siz[x]+=siz[y];
if(siz[y]>siz[son[x]])son[x]=y;
}
}
接下来把轻重儿子连成链,所以我们就一定要让链上的点连续
我们从根开始一遍DFS,如果有重儿子就先走重儿子(将一条重链放到一个区间内),搜到叶子节点后回溯回去再去搜轻儿子(轻链)
板子:
要处理的问题:
- 1将树从x到y结点最短路径上所有节点的值都加上z
- 2求树从x到y结点最短路径上所有节点的值之和
- 3将以x为根节点的子树内所有节点值都加上z
- 4求以x为根节点的子树内所有节点值之和
由于dfs序中一颗子树是连续的一段,3,4就比较好处理了
对于树上任意两点的路径,设所在链顶端的深度更深的那个点为x点
- ans加上x点到x所在链顶端 这一段区间的点权和
- 把x跳到x所在链顶端的那个点的 fa
不停执行这两个步骤,直到两个点处于一条链上,这时再加上此时两个点的区间和即可
(O(log^2n))查询
#include <cstdio>
#include <iostream>
#include <vector>
using namespace std;
#define ls (p<<1)
#define rs (p<<1|1)
const int N=5e5;
typedef long long LL;
inline int read(){
int x=0;char ch=getchar();
while(!isdigit(ch)) ch=getchar();
while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();}
return x;
}
int n,m,root,mod,val[N];
int to[N],nxt[N],hd[N],tot;
inline void add(int x,int y){
to[++tot]=y;nxt[tot]=hd[x];hd[x]=tot;
}
int siz[N],dep[N],fa[N],son[N];
void dfs_son(int x,int f){
siz[x]=1;fa[x]=f;dep[x]=dep[f]+1;
for(int i=hd[x];i;i=nxt[i]){
int y=to[i];
if(y==f) continue;
dfs_son(y,x);
siz[x]+=siz[y];
if(siz[y]>siz[son[x]]) son[x]=y;
}
}
int dfn[N],rev[N],top[N],dfn_cnt;
void dfs_chain(int x,int tp){
dfn[x]=++dfn_cnt;rev[dfn_cnt]=x;top[x]=tp;
if(son[x]) dfs_chain(son[x],tp);
for(int i=hd[x];i;i=nxt[i]){
int y=to[i];
if(dfn[y]) continue;
dfs_chain(y,y);
}
}
struct tree{
int l,r;
LL tag,sum;
}t[N];
inline void push_up(int p){
t[p].sum=(t[ls].sum+t[rs].sum)%mod;
}
void build(int l,int r,int p){
t[p].l=l;t[p].r=r;
if(l==r){ t[p].sum=val[rev[l]];return; }
int mid=(l+r)>>1;
build(l,mid,ls);
build(mid+1,r,rs);
push_up(p);
}
void push_down(int p){
if(!t[p].tag) return;
(t[ls].tag+=t[p].tag)%=mod;
(t[rs].tag+=t[p].tag)%=mod;
(t[ls].sum+=(t[ls].r-t[ls].l+1)*t[p].tag)%=mod;
(t[rs].sum+=(t[rs].r-t[rs].l+1)*t[p].tag)%=mod;
t[p].tag=0;
}
void modify(int L,int R,LL v,int p){
if(L<=t[p].l&&t[p].r<=R){
(t[p].tag+=v)%=mod;
(t[p].sum+=(t[p].r-t[p].l+1)*v)%=mod;
return;
}
push_down(p);
int mid=(t[p].l+t[p].r)>>1;
if(L<=mid) modify(L,R,v,ls);
if(R>mid) modify(L,R,v,rs);
push_up(p);
}
LL query(int L,int R,int p){
if(L<=t[p].l&&t[p].r<=R) return t[p].sum;
push_down(p);
int mid=(t[p].l+t[p].r)>>1;
LL res=0;
if(L<=mid) (res+=query(L,R,ls))%=mod;
if(R>mid) (res+=query(L,R,rs))%=mod;
return res;
}
void update(int x,int y,LL v){
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
modify(dfn[top[x]],dfn[x],v,1);
x=fa[top[x]];
}
if(dfn[x]>dfn[y]) swap(x,y);
modify(dfn[x],dfn[y],v,1);
}
LL sum(int x,int y){
LL res=0;
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
(res+=query(dfn[top[x]],dfn[x],1))%=mod;
x=fa[top[x]];
}
if(dfn[x]>dfn[y]) swap(x,y);
(res+=query(dfn[x],dfn[y],1))%=mod;
return res;
}
int main(){
n=read();m=read();root=read();mod=read();
for(int i=1;i<=n;i++) val[i]=read();
for(int i=1,x,y;i<n;i++){
x=read();y=read();
add(x,y);add(y,x);
}
dfs_son(root,0);
dfs_chain(root,root);
build(1,n,1);
for(int i=1,x,y,z,op;i<=m;i++){
op=read();x=read();
if(op==1){
y=read();z=read();
update(x,y,z);
}
if(op==2){
y=read();
printf("%lld
",sum(x,y));
}
if(op==3){
z=read();
modify(dfn[x],dfn[x]+siz[x]-1,z,1);
}
if(op==4){
printf("%lld
",query(dfn[x],dfn[x]+siz[x]-1,1));
}
}
return 0;
}
类板子:
https://www.luogu.com.cn/problem/P3178
https://www.luogu.com.cn/problem/P2590
https://www.luogu.com.cn/problem/P3128
边权转化:
Qtree1 具体的把边权赋给深度较深的点(在dfs_son时),但有个问题是,我们查 (x,y) 上的最大值,其lca维护的是 lca-->fa[lca] 的边权,实际是不可查到的,所以我们只需在查询最后一步
https://www.luogu.com.cn/problem/P303
类似上面
软件包管理器
安装—— 1到x的路径赋值为1
卸载—— x的子树赋值为0
ans=操作前的总和和操作后的总和
#include<bits/stdc++.h>
using namespace std;
#define N 100010
#define ls (p<<1)
#define rs (p<<1|1)
inline int read() {
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)) {if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();}
return f*x;
}
int n,q;
char op[10];
int to[N<<1],nxt[N<<1],hd[N],tot;
inline void add(int x,int y) {
to[++tot]=y;nxt[tot]=hd[x];hd[x]=tot;
}
int siz[N],fa[N],son[N],dep[N];
void dfs_son(int x,int f) {
siz[x]=1;fa[x]=f;dep[x]=dep[f]+1;
for(int i=hd[x];i;i=nxt[i]) {
int y=to[i];
if(y==f)continue;
dfs_son(y,x);
siz[x]+=siz[y];
if(siz[y]>siz[son[x]])son[x]=y;
}
}
int dfn[N],top[N],dfn_cnt;
void dfs_chain(int x,int tp) {
top[x]=tp;
dfn[x]=++dfn_cnt;
if(son[x])dfs_chain(son[x],tp);
for(int i=hd[x];i;i=nxt[i]) {
int y=to[i];
if(dfn[y])continue;
dfs_chain(y,y);
}
}
struct TREE{
int l,r,sum,tag;
}t[N<<2];
void pushdown(int p) {
if(t[p].tag==-1)return;
t[ls].tag=t[p].tag;
t[rs].tag=t[p].tag;
t[ls].sum=t[p].tag*(t[ls].r-t[ls].l+1);
t[rs].sum=t[p].tag*(t[rs].r-t[rs].l+1);
t[p].tag=-1;
}
void build(int L,int R,int p) {
t[p].l=L;t[p].r=R;t[p].tag=-1;
if(L==R) return;
int mid=(L+R)>>1;
build(L,mid,ls);
build(mid+1,R,rs);
t[p].sum=t[ls].sum+t[rs].sum;
}
void modify(int L,int R,int add,int p) {
if(L<=t[p].l&&t[p].r<=R) {
t[p].sum=add*(t[p].r-t[p].l+1);
t[p].tag=add;return;
}
pushdown(p);
int mid=(t[p].l+t[p].r)>>1;
if(L<=mid) modify(L,R,add,ls);
if(mid<R) modify(L,R,add,rs);
t[p].sum=t[ls].sum+t[rs].sum;
}
void update(int x,int y,int add) {
while(top[x]!=top[y]) {
if(dep[top[x]]<dep[top[y]]) swap(x,y);
modify(dfn[top[x]],dfn[x],add,1);
x=fa[top[x]];
}
if(dfn[x]>dfn[y]) swap(x,y);
modify(dfn[x],dfn[y],add,1);
}
int main() {
n=read();
for(int i=2,x;i<=n;++i) {
x=read()+1;
add(x,i),add(i,x);
}
dfs_son(1,0);
dfs_chain(1,1);
build(1,n,1);
q=read();
while(q--) {
int a,bef;
bef=t[1].sum;
scanf("%s",op);
a=read()+1;
if(op[0]=='i') {
update(1,a,1);
printf("%d
",abs(bef-t[1].sum));
} else {
modify(dfn[a],dfn[a]+siz[a]-1,0,1);
printf("%d
",abs(bef-t[1].sum));
}
}
return 0;
}
染色
好题!!
细节好多哦
就是要维护个lcol,rcol
每次合并(包括询问合并)的时候
if(t[ls].rc==t[rs].lc) ans--
#include<bits/stdc++.h>
using namespace std;
#define N 100010
#define ls (p<<1)
#define rs (p<<1|1)
inline int read() {
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)) {if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();}
return f*x;
}
int n,q,a[N];
int to[N<<1],nxt[N<<1],hd[N],tot;
inline void add(int x,int y) {
to[++tot]=y;nxt[tot]=hd[x];hd[x]=tot;
}
int siz[N],fa[N],son[N],dep[N];
void dfs_son(int x,int f) {
siz[x]=1;fa[x]=f;dep[x]=dep[f]+1;
for(int i=hd[x];i;i=nxt[i]) {
int y=to[i];
if(y==f)continue;
dfs_son(y,x);
siz[x]+=siz[y];
if(siz[y]>siz[son[x]])son[x]=y;
}
}
int dfn[N],rev[N],top[N],dfn_cnt;
void dfs_chain(int x,int tp) {
top[x]=tp;
dfn[x]=++dfn_cnt;rev[dfn_cnt]=x;
if(son[x])dfs_chain(son[x],tp);
for(int i=hd[x];i;i=nxt[i]) {
int y=to[i];
if(dfn[y])continue;
dfs_chain(y,y);
}
}
struct TREE{
int val,lc,rc,l,r,tag;
}t[N<<2];
inline void pushup(int p) {
t[p].val=t[ls].val+t[rs].val-(t[ls].rc==t[rs].lc);
t[p].lc=t[ls].lc;t[p].rc=t[rs].rc;//Q
}
void pushdown(int p) {//Q
if(t[p].tag==-1)return;
t[ls].tag=t[rs].tag=t[p].tag;
t[ls].val=t[rs].val=1;
t[ls].lc=t[ls].rc=t[p].tag;
t[rs].lc=t[rs].rc=t[p].tag;
t[p].tag=-1;
}
void build(int L,int R,int p) {
t[p].l=L;t[p].r=R;t[p].tag=-1;
if(L==R) {//Q
t[p].val=1;
t[p].lc=t[p].rc=a[rev[L]];
return;
}
int mid=(L+R)>>1;
build(L,mid,ls);
build(mid+1,R,rs);
pushup(p);
}
void modify(int L,int R,int add,int p) {
if(L<=t[p].l&&t[p].r<=R) {//Q
t[p].val=1;
t[p].lc=t[p].rc=t[p].tag=add;
return;
}
pushdown(p);
int mid=(t[p].l+t[p].r)>>1;
if(L<=mid) modify(L,R,add,ls);
if(mid<R) modify(L,R,add,rs);
pushup(p);
}
TREE query(int L,int R,int p) {
if(L<=t[p].l&&t[p].r<=R) return t[p];
pushdown(p);
int mid=(t[p].l+t[p].r)>>1;
if(R<=mid) return query(L,R,ls);
else if(L>mid) return query(L,R,rs);
else {//Q
TREE s1=query(L,R,ls),s2=query(L,R,rs),s;
s.val=s1.val+s2.val-(s1.rc==s2.lc);
s.lc=s1.lc,s.rc=s2.rc;
return s;
}
}
void upd(int x,int y,int add) {
while(top[x]!=top[y]) {
if(dep[top[x]]<dep[top[y]]) swap(x,y);
modify(dfn[top[x]],dfn[x],add,1);
x=fa[top[x]];
}
if(dfn[x]>dfn[y]) swap(x,y);
modify(dfn[x],dfn[y],add,1);
}
int get(int x,int y) {
int ans=0,lc=0,rc=0;TREE s;
while(top[x]!=top[y]) {
if(dep[top[x]]<dep[top[y]]) swap(x,y),swap(lc,rc);//Qswap
s=query(dfn[top[x]],dfn[x],1);
ans+=s.val-(s.rc==lc);//Q
lc=s.lc;
x=fa[top[x]];
}
if(dfn[x]>dfn[y]) swap(x,y),swap(lc,rc);//Qswap
s=query(dfn[x],dfn[y],1);
return ans+s.val-(s.lc==lc)-(s.rc==rc);//Q
}
int main() {
n=read();q=read();
for(int i=1;i<=n;i++)
a[i]=read();
for(int i=2,x,y;i<=n;++i) {
x=read();y=read();
add(x,y),add(y,x);
}
dfs_son(1,0);
dfs_chain(1,1);
build(1,n,1);
char op;int a,b,c;
while(q--) {
cin>>op;a=read();b=read();
if(op=='C') {
c=read();
upd(a,b,c);
} else {
printf("%d
",get(a,b));
}
}
return 0;
}
LNOI2014LCA
这题统计 l~r 中所有点与z的lca的深度之和。
暴力就是把lca都求出来。。。显然这题没有暴力分
所以正解要么是一次求出多个lca不会,要么就是把这个求多个dep的和转化一下。
dep[i] 其实就是 i 到根有几个点
比较暴力的方法:我们不妨把 z 到根的路径上的点全部 +1,对于 l 到 r 之间的点询问他们到根路径上的点权和。上面的暴力具有叠加性,且可逆。也就是说我们可以对于 l 到 r 之间的点 i,将 i 到根的路径上的点全部 +1, 转而询问 z 到根的路径上的点(包括自身)的权值和就是这个询问的答案。
但是考虑到每次统计时,不能很好的排除 l ~ r 区间之外的点对 z->根 这条路径的贡献,所以我们每次都要清空线段树。
我们每次清空线段树,然后从 l ~ r 再添加一遍,树剖+线段树的复杂度就是 O(n * logn * logn)的,还要做 q 次,复杂度依然不理想。
把询问差分下,也就是用 [1, r] − [1, l − 1] 来计算答案,每个拆开的区间之间是有重叠的,是可以转移的,而不用每次都清空。
所以我们可以将差分后的区间按照端点从小到大排序(左端点都是根),然后按从小到大的顺序添加点,每遇到一个询问就查询一次,从而排除掉区间之外的点的影响,也就优化掉一个 q 的复杂度。
#include <queue>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#define ls (p<<1)
#define rs (p<<1|1)
#define mid ((l+r)>>1)
const int N=100005;
inline int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return f*x;
}
int n,m;
int to[N<<1],nxt[N<<1],hd[N],tot;
inline void add(int x,int y) {
to[++tot]=y;nxt[tot]=hd[x];hd[x]=tot;
}
int siz[N],fa[N],son[N],dep[N];
void dfs_son(int x,int f) {
siz[x]=1;fa[x]=f;dep[x]=dep[f]+1;
for(int i=hd[x];i;i=nxt[i]) {
int y=to[i];
if(y==f)continue;
dfs_son(y,x);
siz[x]+=siz[y];
if(siz[y]>siz[son[x]])son[x]=y;
}
}
int dfn[N],rev[N],top[N],dfn_cnt;
void dfs_chain(int x,int tp) {
top[x]=tp;
dfn[x]=++dfn_cnt;rev[dfn_cnt]=x;
if(son[x])dfs_chain(son[x],tp);
for(int i=hd[x];i;i=nxt[i]) {
int y=to[i];
if(dfn[y])continue;
dfs_chain(y,y);
}
}
struct TREE{
int len,sum,tag;
}t[N<<2];
struct node{
int ans,z;
}q[N];
void build(int l,int r,int p) {
t[p].len=r-l+1;
if(l==r) return;
build(l,mid,ls);
build(mid+1,r,rs);
}
void pushdown(int p) {
if(!t[p].tag) return;
t[ls].tag+=t[p].tag;
t[rs].tag+=t[p].tag;
t[ls].sum+=t[p].tag*t[ls].len;
t[rs].sum+=t[p].tag*t[rs].len;
t[p].tag=0;
}
void modify(int l,int r,int L,int R,int p) {
if(L<=l&&r<=R) {
t[p].tag++;
t[p].sum+=t[p].len;
return;
}
pushdown(p);
if(L<=mid) modify(l,mid,L,R,ls);
if(R>mid) modify(mid+1,r,L,R,rs);
t[p].sum=t[ls].sum+t[rs].sum;
}
void upd(int x,int y) {
while(top[x]!=top[y]) {
if(dep[top[x]]<dep[top[y]]) swap(x,y);
modify(1,n,dfn[top[x]],dfn[x],1);
x=fa[top[x]];
}
if(dfn[x]>dfn[y]) swap(x,y);
modify(1,n,dfn[x],dfn[y],1);
}
int query(int l,int r,int L,int R,int p) {
if(L<=l&&r<=R) return t[p].sum;
pushdown(p);
int ans=0;
if(L<=mid) ans+=query(l,mid,L,R,ls);
if(R>mid) ans+=query(mid+1,r,L,R,rs);
return ans;
}
int getsum(int x,int y) {
int ans=0;
while(top[x]!=top[y]) {
if(dep[top[x]]<dep[top[y]]) swap(x,y);
ans+=query(1,n,dfn[top[x]],dfn[x],1);
x=fa[top[x]];
}
if(dfn[x]>dfn[y]) swap(x,y);
return ans+query(1,n,dfn[x],dfn[y],1);
}
struct QUES{
int p,id;bool flag;
QUES() {}
QUES(int p_,int id_,bool flag_):p(p_),id(id_),flag(flag_){}
bool operator < (const QUES &x) const {
return p<x.p;
}
}a[N];
int main(){
n=read();m=read();
for(int i=2,x;i<=n;i++) {
x=read()+1;
add(i,x);add(x,i);
}
dfs_son(1,0);
dfs_chain(1,1);
build(1,n,1);
for(int i=1;i<=m;i++) {
a[i*2-1]=QUES(read(),i,0);
a[i*2]=QUES(read()+1,i,1);
q[i].z=read()+1;
}
sort(a+1,a+1+2*m);
int now=0;
for(int i=1;i<=2*m;i++) {
while(now<a[i].p) {
now++;
upd(1,now);
}
int r=getsum(1,q[a[i].id].z);
q[a[i].id].ans+=a[i].flag?r:(-r);
}
for(int i=1;i<=m;i++)
printf("%d
",q[i].ans%201314);
return 0;
}
松鼠的新家
树剖写法(差分更简单)
#include <cstdio>
#include <iostream>
#include <vector>
using namespace std;
#define ls (p<<1)
#define rs (p<<1|1)
const int N=5e6;
inline int read(){
int x=0;char ch=getchar();
while(!isdigit(ch)) ch=getchar();
while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();}
return x;
}
int n,val[N],ans;
int to[N],nxt[N],hd[N],tot;
inline void add(int x,int y){
to[++tot]=y;nxt[tot]=hd[x];hd[x]=tot;
}
int siz[N],dep[N],fa[N],son[N];
void dfs_son(int x,int f){
siz[x]=1;fa[x]=f;dep[x]=dep[f]+1;
for(int i=hd[x];i;i=nxt[i]){
int y=to[i];
if(y==f) continue;
dfs_son(y,x);
siz[x]+=siz[y];
if(siz[y]>siz[son[x]]) son[x]=y;
}
}
int dfn[N],rev[N],top[N],dfn_cnt;
void dfs_chain(int x,int tp){
dfn[x]=++dfn_cnt;rev[dfn_cnt]=x;top[x]=tp;
if(son[x]) dfs_chain(son[x],tp);
for(int i=hd[x];i;i=nxt[i]){
int y=to[i];
if(dfn[y]) continue;
dfs_chain(y,y);
}
}
struct tree{
int l,r;
int tag,sum;
}t[N];
inline void push_up(int p){
t[p].sum=(t[ls].sum+t[rs].sum);
}
void build(int l,int r,int p){
t[p].l=l;t[p].r=r;
if(l==r) return;
int mid=(l+r)>>1;
build(l,mid,ls);
build(mid+1,r,rs);
push_up(p);
}
void push_down(int p){
if(!t[p].tag) return;
t[ls].tag+=t[p].tag;
t[rs].tag+=t[p].tag;
t[ls].sum+=(t[ls].r-t[ls].l+1)*t[p].tag;
t[rs].sum+=(t[rs].r-t[rs].l+1)*t[p].tag;
t[p].tag=0;
}
void modify(int L,int R,int v,int p){
if(L<=t[p].l&&t[p].r<=R){
t[p].tag+=v;
t[p].sum+=(t[p].r-t[p].l+1)*v;
return;
}
push_down(p);
int mid=(t[p].l+t[p].r)>>1;
if(L<=mid) modify(L,R,v,ls);
if(R>mid) modify(L,R,v,rs);
push_up(p);
}
int query(int L,int R,int p){
if(L<=t[p].l&&t[p].r<=R) return t[p].sum;
push_down(p);
int mid=(t[p].l+t[p].r)>>1;
int res=0;
if(L<=mid) res+=query(L,R,ls);
if(R>mid) res+=query(L,R,rs);
return res;
}
void update(int x,int y,int v){
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
modify(dfn[top[x]],dfn[x],v,1);
x=fa[top[x]];
}
if(dfn[x]>dfn[y]) swap(x,y);
modify(dfn[x],dfn[y],v,1);
}
int main(){
n=read();
for(int i=1;i<=n;i++) val[i]=read();
for(int i=1,x,y;i<n;i++){
x=read();y=read();
add(x,y);add(y,x);
}
dfs_son(1,0);
dfs_chain(1,1);
build(1,n,1);
for(int i=1;i<n;i++){
int x=val[i],y=val[i+1];
update(x,y,1);
update(y,y,-1);
}
for(int i=1;i<=n;i++){
ans=query(dfn[i],dfn[i],1);
printf("%d
",ans);
}
return 0;
}