圆方树
重要的:::注意点权赋值
在一般无向图上使用它
•配合点双连通分量缩点用的
•对于一个dcc,建立一个方点,dcc内所有点向他连边
•割点关联多个dcc,连接多个方点
•这样会形成一棵树,实际上dcc缩点可以有不同的建树方式
圆方树的点数小于 2n,这是因为割点的数量小于 n,所以请注意各种数组大小要开两倍。
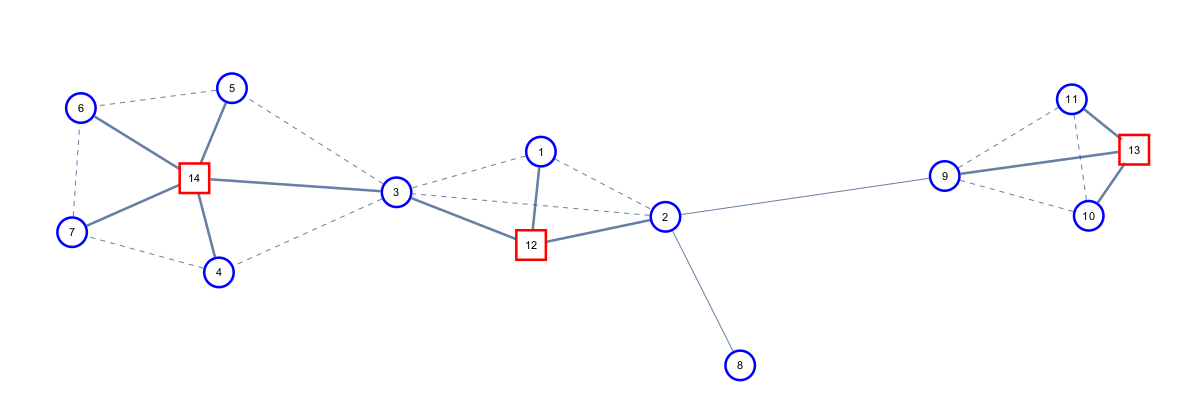
图一:原图,图二:标出点双,图三:圆方树
建树代码
void tarjan(int x) {
vis[x]=1;
cnt_size++;//非联通图处理每个连通块
st[++top]=x;
dfn[x]=low[x]=++dfn_cnt;
for(int i=hd[x];i;i=nxt[i]) {
int y=to[i];
if(!dfn[y]) {
tarjan(y);
low[x]=min(low[x],low[y]);
if(low[y]==dfn[x]) {//找到一个以x为根的点双连通分量
w[++num]=0;//num为方点的编号,初始值为n
while(st[top+1]!=y) {//将点双中除了x的点退栈,并在圆方树中连边
G[num].push_back(st[top]);
G[st[top]].push_back(num);
vis[st[top--]]=0;
++w[num];
}//注意x自身也要连边(但不退栈)
G[num].push_back(x);
G[x].push_back(num);
++w[num];
}
} else if(vis[y])low[x]=min(low[x],dfn[y]);
}
}
https://www.luogu.com.cn/problem/CF1062F
没懂
显然,一个点是重要的点或者次重要的点,那么和它在同一个 scc 内的所有点一定也是重要 的或者次重要的,那么可以仅考虑这个 scc 整体 既然我只需要考虑可达性,那么可以缩点 考虑这个 dag 的拓扑序,重要的点前面的点一定能到达它,它一定能到达后面的点 考虑拓扑排序的过程,当重要的点出队时,由于它能到达后面的所有点,这些点必须由它这 个“祖先”(当然这用在 dag 上不太合适……)扩展出来,所以这时队列一定是空的 这样我们对正图和反图分别拓扑排序(必须保证前后都能成为“祖先”)就能找到重要的点 对于次重要的点,显然被删的那点不可能属于一个大的 scc,一定是一个孤立的点 也就是说,对于一个次重要点只有这么一个孤立点,他俩不能互相到达 这样的话,拓扑排序让这点出队时,队里最多只能剩下这么一个孤立点,这可以画几个例子 理解一下,这样就可以找了 对于 dag,或者缩点之后的 dag,我一定要考虑拓扑排序,你 dp 不也得这么干啊
铁人两项
题解见参考blog1
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N=200005;
const int M=400005;
inline int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return f*x;
}
int n,m,num;
int hd[N],nxt[M],to[M],tot;
inline void add(int x,int y) {
to[++tot]=y;nxt[tot]=hd[x];hd[x]=tot;
}
int dfn[N],low[N],dfn_cnt;
int st[N],top,cnt_size;//连通块内点数
int w[N];
bool vis[N];
vector<int>G[N];
void tarjan(int x) {
vis[x]=1;
cnt_size++;
st[++top]=x;
dfn[x]=low[x]=++dfn_cnt;
for(int i=hd[x];i;i=nxt[i]) {
int y=to[i];
if(!dfn[y]) {
tarjan(y);
low[x]=min(low[x],low[y]);
if(low[y]==dfn[x]) {
w[++num]=0;
while(st[top+1]!=y) {
G[num].push_back(st[top]);
G[st[top]].push_back(num);
vis[st[top--]]=0;
++w[num];
// top--;
}
G[num].push_back(x);
G[x].push_back(num);
++w[num];
}
} else if(vis[y])low[x]=min(low[x],dfn[y]);
}
}
long long ans;
int siz[N];
void dfs(int x,int fa) {
siz[x]=(x<=n);
for(int i=0;i<G[x].size();i++) {
int y=G[x][i];
if(y==fa) continue;
dfs(y,x);
ans+=2ll*w[x]*siz[x]*siz[y];
siz[x]+=siz[y];
}
ans+=2ll*w[x]*siz[x]*(cnt_size-siz[x]);
}
int main() {
n=read();m=read();
for(int i=1;i<=n;i++) w[i]=-1;
num=n;//编号
for(int i=1,x,y;i<=m;i++) {
x=read();y=read();
add(x,y),add(y,x);
}
for(int i=1;i<=n;i++)
if(!dfn[i]) {
cnt_size=0;
tarjan(i);
--top;
dfs(i,0);
}
printf("%lld
",ans);
return 0;
}
[CodeForces 487E]Tourists
见参考blog1
建出原图的圆方树,令方点权值为相邻圆点权值的最小值,问题转化为求路径上最小值
一次修改一个圆点的点权,需要修改所有和它相邻的方点,这样很容易被卡到 O(n) 个修改。
但是注意到这样的作为方点父亲的圆点只会在当方点是 s 和 t 的 lca 时才会影响答案,令方点权值为自己的儿子圆点的权值最小值,这样的话修改时只需要修改父亲方点,而在查询时特判一下 lca 方点的父亲即可 这种“考虑何时会对答案产生影响”的思路是相当重要的
对于方点的维护,只需要对每个方点开一个 multiset 维护权值集合即可。
#include <set>
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N=200005;
const int M=400005;
inline int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return f*x;
}
int n,m,q,num;
int hd[N],nxt[M],to[M],tot;
inline void add(int x,int y) {
to[++tot]=y;nxt[tot]=hd[x];hd[x]=tot;
}
int dfn[N],low[N],dfn_cnt;
int st[N],tp;
bool vis[N];
vector<int>G[N];
void tarjan(int x) {
vis[x]=1;
st[++tp]=x;
dfn[x]=low[x]=++dfn_cnt;
for(int i=hd[x];i;i=nxt[i]) {
int y=to[i];
if(!dfn[y]) {
tarjan(y);
low[x]=min(low[x],low[y]);
if(low[y]==dfn[x]) {
++num;
while(st[tp+1]!=y) {
G[num].push_back(st[tp]);
G[st[tp]].push_back(num);
vis[st[tp--]]=0;
}
G[num].push_back(x);
G[x].push_back(num);
}
} else if(vis[y])low[x]=min(low[x],dfn[y]);
}
}
multiset<int>s[N];
int siz[N],fa[N],dep[N],son[N];
void dfs_son(int x,int f) {
fa[x]=f;siz[x]=1;dep[x]=dep[f]+1;
for(int i=0;i<G[x].size();i++) {
int y=G[x][i];
if(y==f) continue;
dfs_son(y,x);
siz[x]+=siz[y];
if(siz[y]>siz[son[x]]) son[x]=y;
}
}
int rev[N],top[N];
void dfs_chain(int x,int tp) {
top[x]=tp;
dfn[x]=++dfn_cnt;rev[dfn_cnt]=x;
if(son[x]) dfs_chain(son[x],tp);
for(int i=0;i<G[x].size();i++) {
int y=G[x][i];
if(y==fa[x]||y==son[x]) continue;
dfs_chain(y,y);
}
}
#define ls (p<<1)
#define rs (p<<1|1)
#define mid ((l+r)>>1)
int val[N<<2];
int w[N];
void build(int l,int r,int p) {
if(l==r) {val[p]=w[rev[l]];return;}
build(l,mid,ls);
build(mid+1,r,rs);
val[p]=min(val[ls],val[rs]);
}
void modify(int l,int r,int t,int v,int p) {
if(l==r) {val[p]=v;return;}
if(t<=mid) modify(l,mid,t,v,ls);
else modify(mid+1,r,t,v,rs);
val[p]=min(val[ls],val[rs]);
}
int query(int l,int r,int L,int R,int p) {
if(L<=l&&r<=R) return val[p];
int ans=0x3f3f3f3f;
if(L<=mid) ans=min(ans,query(l,mid,L,R,ls));
if(R>mid) ans=min(ans,query(mid+1,r,L,R,rs));
return ans;
}
int get_min(int x,int y) {
int ans=0x3f3f3f3f;
while(top[x]!=top[y]) {
if(dep[top[x]]<dep[top[y]]) swap(x,y);
ans=min(ans,query(1,num,dfn[top[x]],dfn[x],1));
x=fa[top[x]];
}
if(dfn[x]>dfn[y]) swap(x,y);
ans=min(ans,query(1,num,dfn[x],dfn[y],1));
if(x>n) ans=min(ans,w[fa[x]]);//Q
return ans;
}
int main() {
n=read();m=read();q=read();
for(int i=1;i<=n;i++) w[i]=read();
num=n;//编号
for(int i=1,x,y;i<=m;i++) {
x=read();y=read();
add(x,y),add(y,x);
}
tarjan(1);
dfn_cnt=0;
dfs_son(1,0);
dfs_chain(1,1);
for(int i=1;i<=n;i++)
if(fa[i]) s[fa[i]].insert(w[i]);
for(int i=n+1;i<=num;i++)
w[i]=*s[i].begin();
memset(val,0x3f,sizeof(val));
build(1,num,1);
char op;int x,y;
while(q--) {
cin>>op;x=read();y=read();
if(op=='C') {
modify(1,num,dfn[x],y,1);
if(fa[x]) {
s[fa[x]].erase(s[fa[x]].lower_bound(w[x]));
s[fa[x]].insert(y);
if(w[fa[x]]!=*s[fa[x]].begin()) {
w[fa[x]]=*s[fa[x]].begin();
modify(1,num,dfn[fa[x]],w[fa[x]],1);
}
}
w[x]=y;
}
else printf("%d
",get_min(x,y));
}
return 0;
}
wait
#include <cstdio>
#include <vector>
#include <algorithm>
const int MN = 100005;
int N, M, Q, cnt;
std::vector<int> G[MN], T[MN * 2];
int dfn[MN * 2], low[MN], dfc;
int stk[MN], tp;
void Tarjan(int u) {
low[u] = dfn[u] = ++dfc;
stk[++tp] = u;
for (auto v : G[u]) {
if (!dfn[v]) {
Tarjan(v);
low[u] = std::min(low[u], low[v]);
if (low[v] == dfn[u]) {
++cnt;
for (int x = 0; x != v; --tp) {
x = stk[tp];
T[cnt].push_back(x);
T[x].push_back(cnt);
}
T[cnt].push_back(u);
T[u].push_back(cnt);
}
}
else low[u] = std::min(low[u], dfn[v]);
}
}
int dep[MN * 2], faz[MN * 2][18], dis[MN * 2];
void DFS(int u, int fz) {
dfn[u] = ++dfc;
dep[u] = dep[faz[u][0] = fz] + 1;
dis[u] = dis[fz] + (u <= N);
for (int j = 0; j < 17; ++j)
faz[u][j + 1] = faz[faz[u][j]][j];
for (auto v : T[u]) if (v != fz) DFS(v, u);
}
int LCA(int x, int y) {
if (dep[x] < dep[y]) std::swap(x, y);
for (int j = 0, d = dep[x] - dep[y]; d; ++j, d >>= 1)
if (d & 1) x = faz[x][j];
if (x == y) return x;
for (int j = 17; ~j; --j)
if (faz[x][j] != faz[y][j])
x = faz[x][j], y = faz[y][j];
return faz[x][0];
}
int main() {
int Ti; scanf("%d", &Ti);
while (Ti--) {
scanf("%d%d", &N, &M);
for (int i = 1; i <= N; ++i) {
G[i].clear();
dfn[i] = low[i] = 0;
}
for (int i = 1; i <= N * 2; ++i) T[i].clear();
for (int i = 1, x, y; i <= M; ++i) {
scanf("%d%d", &x, &y);
G[x].push_back(y);
G[y].push_back(x);
}
cnt = N;
dfc = 0, Tarjan(1), --tp;
dfc = 0, DFS(1, 0);
scanf("%d", &Q);
while (Q--) {
static int S, A[MN];
scanf("%d", &S);
int Ans = -2 * S;
for (int i = 1; i <= S; ++i) scanf("%d", &A[i]);
std::sort(A + 1, A + S + 1, [](int i, int j) { return dfn[i] < dfn[j]; });
for (int i = 1; i <= S; ++i) {
int u = A[i], v = A[i % S + 1];
Ans += dis[u] + dis[v] - 2 * dis[LCA(u, v)];
}
if (LCA(A[1], A[S]) <= N) Ans += 2;
printf("%d
", Ans / 2);
}
}
return 0;
}
参考blog
https://www.cnblogs.com/PinkRabbit/p/10446473.html
https://www.cnblogs.com/cjyyb/p/9098400.html ————仙人掌+圆方树