Pytorch学习：线性回归

本次学习实现线性回归。

采用两种方法实现，第一种为手动方法，第二种为pytorch的autograd方法。

一、手动实现线性回归

导入对应包

import torch as t
%matplotlib inline
from matplotlib import pyplot as plt
from IPython import display

产生对应的随机数据

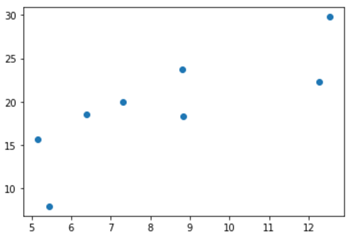
# 设置随机数种子，保证在不同计算机上运行时下面的输出一致
t.manual_seed(1000)

def get_fake_data(batch_size=8):
    #参数随机数据:y=x*2+3，加上随机噪声
    x=t.rand(batch_size,1)*20
    y=x*2+(1+t.randn(batch_size,1))*3
    return x,y

x,y=get_fake_data()
plt.scatter(x.squeeze().numpy(), y.squeeze().numpy())

运行效果如下，生成一个batch的含噪声随机点

初始化参数，开始手动进行梯度下降

#随机初始化参数
w=t.rand(1,1)
b=t.zeros(1,1)

lr=0.001 #学习率

for ii in range(20000):
    x,y=get_fake_data()
    
    # forward: 计算loss
    y_pred=x.mm(w)+b.expand_as(y)
    loss=0.5*(y_pred-y)**2   #均方误差
    loss=loss.sum()
    
    # backward :手动计算梯度
    dloss=1
    dy_pred=dloss*(y_pred-y)
    
    dw=x.t().mm(dy_pred)
    db=dy_pred.sum()
    
    #更新参数
    w.sub_(lr*dw)
    b.sub_(lr*db)
    
    if ii%1000==0:
        
        #画图
        display.clear_output(wait=True)
        x=t.arange(0.,20.).view(-1,1)
        y=x.mm(w)+b.expand_as(x)
        plt.plot(x.numpy(),y.numpy())
        
        x2,y2=get_fake_data(batch_size=20)
        plt.scatter(x2.numpy(),y2.numpy())
        
        plt.xlim(0,20)
        plt.ylim(0,41)
        plt.show()
        plt.pause(0.5)
print(w.squeeze().item(),b.squeeze().item())

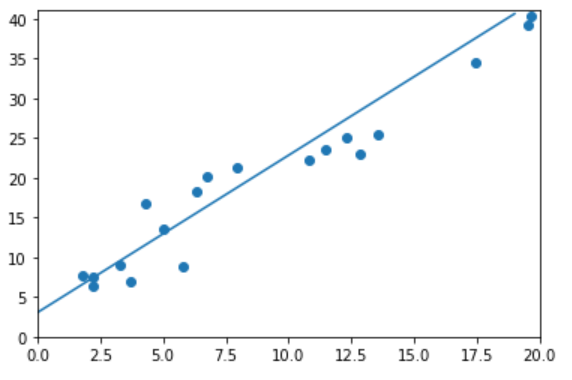
运行效果图如下，其中离散点是含有噪声的真实数据，直线是对应w,b画出的直线。

最后得出的拟合结果为：

2.114304542541504 3.0964057445526123

可以看出已经非常接近预先设定的参数,w=2,b=3

 

二、使用Variable实现线性回归

pytorch的自动求导功能很强大，可以代替手工求导。

下面我们使用Variable的autograd功能实现自动求导。

 

导入对应包

import torch as t
from torch.autograd import Variable as V
%matplotlib inline
from matplotlib import pyplot as plt
from IPython import display

设置参数w和b为Variable变量

w=V(t.rand(1,1),requires_grad=True)
b=V(t.zeros(1,1),requires_grad=True)

lr=0.001 #学习率

开始自动求导

for ii in range(8000):
    x,y=get_fake_data()
    x,y=V(x),V(y)
    
    #forward: 计算loss
    y_pred=x.mm(w)+b.expand_as(y)
    loss=0.5*(y_pred-y)**2
    loss=loss.sum()
    
    # backward : 自动计算梯度
    loss.backward()
    
    #更新参数
    w.data.sub_(lr*w.grad.data)
    b.data.sub_(lr*b.grad.data)
    
    #梯度清零
    w.grad.data.zero_()
    b.grad.data.zero_()
    
    if ii%1000 ==0:
        #画图
        display.clear_output(wait=True)
        x=t.arange(0.,20.).view(-1,1)
        y=x.mm(w.data)+b.data.expand_as(x)
        plt.plot(x.numpy(), y.numpy())
        
        x2,y2=get_fake_data(batch_size=20)
        plt.scatter(x2.numpy(),y2.numpy())
        
        plt.xlim(0,20)
        plt.ylim(0,41)
        plt.show()
        plt.pause(0.5)
print(w.data.squeeze().item(),b.data.squeeze().item())

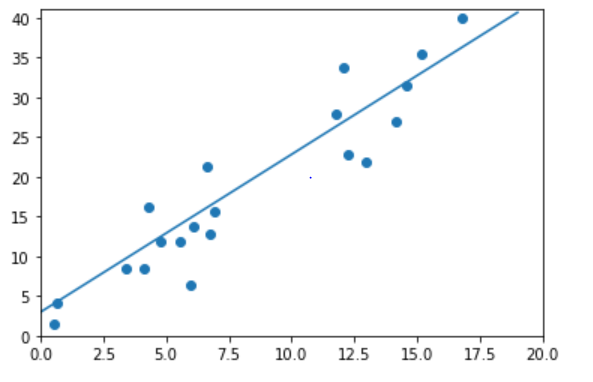
学习的效果图如下：

w和b的值：2.0919859409332275 2.9494316577911377

可以看出，自动求导也可以获得较好的效果。

本次使用的函数较为简单，手动求导还比较方便。对于较为复杂的函数，

尽量使用pytorch的自动求导功能，还是很强大的。