一、齐次变换
1、平移变换
变换矩阵不能包含X,Y,Z等坐标变量
如果x坐标向右平移了5个单位长度,则x~=x+5。在变换矩阵中表示的时候添加一个w坐标变量。通过加入一个w坐标,可以实现平移变换

1>如果w>0,这表示一个真实物理世界的点,因为你可以用x,y,z三个坐标初一w得到这个真是的点。
2>如果w=0,表示一个无穷远处的点
3>在实际应用中,w等于0通常用来表示一个向量
齐次坐标的优点:只需在渲染管线的最后做一次 除法(除以w)就能将齐次坐标转换为非齐次。
一般的平移矩阵:

可以简写为2*2的矩阵,左上角是一个3*3的单位矩阵,T和0是向量,1是数值。
旋转总是相对于原点!!先做旋转再做平移,因为矩阵乘法是不可交换的
2、齐次坐标
齐次坐标的形式:简而言之,齐次坐标就是用N+1维来代表N维坐标
齐次坐标在电脑图形内无处不在,因为该坐标允许平移、旋转、缩放及透视投影等可表示为矩阵与向量相乘的一般向量运算。
我们可以在一个2D笛卡尔坐标末尾加上一个额外的变量w来形成2D齐次坐标,因此,一个点(X,Y)在齐次坐标里面变成了(x,y,w),并且有
X = x/w
Y = y/w
我们把齐次坐标转化为笛卡尔坐标的方法是前面n-1个坐标分量分别除以最后一个分量即可。
例如,笛卡尔坐标系下(1,2)的齐次坐标可以表示为(1,2,1),如果点(1,2)移动到无限远处,在笛卡尔坐标下它变为(∞,∞),然后它的齐次坐标表示为(1,2,0),因为(1/0, 2/0) = (∞,∞),我们可以不用”∞"来表示一个无穷远处的点了
3、旋转变换
先平移再旋转的结果: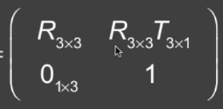
先旋转再平移的结果:
例题:

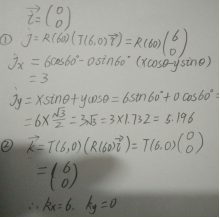
解:因为所变换的向量在后边,所以j是先平移再旋转,k是先旋转再平移,利用平移公式与旋转公式得出结果。
二、法向变换
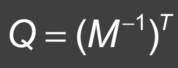
这个公式要施加到曲面上所有的法向上,产生法向变换
例题:

解:
与M相关的法向变换Q=(M^−1)^T。
对于这里的旋转矩阵 R(a⃗ ,θ), 逆矩阵等于绕着相同的旋转轴旋转 −θ:
R(a⃗ ,θ)^−1=R(a⃗ ,−θ)
对这个矩阵转置产生相似的结果:R(a⃗ ,θ)^T=R(a⃗ ,−θ)
(R(a⃗ ,θ)^T=R(a⃗,θ)^−1 是旋转矩阵的一个特殊属性。)
组织起来我们得到:
R(a⃗,θ)^−T=R(a⃗,θ)
三、旋转和坐标系
坐标系分为世界坐标系和相机坐标系
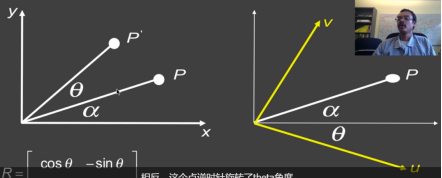
图一可看成P点逆时针旋转了θ角度,而图二可以看成坐标轴顺时针旋转了θ角度
从u,v轴分别向x,y轴画垂线,假设u,v长度为单位1,则u的坐标为(cosθ,-sinθ),v(sinθ,cosθ),对应旋转矩阵的数值
旋转矩阵的行可以看成新坐标轴的坐标

轴角公式:

例题:

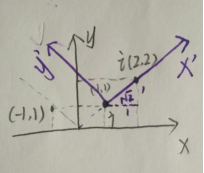
图解如下图所示:
现将标准坐标轴原点移动到新的原点处,根据新x,y画出新x,y轴的方向(也可以根据上边公式得出),i点当好在新x轴上,(根号2,0)
四、推导GLULOOKAT
1、定义:gluLookAt是OpenGL中观察变换的一个关键函数。
2、gluLookAt矩阵可以简要总结为:gluLookAt矩阵可以认为先将相机/视点平移到原点,然后绕着原点旋转,使得相机可以观察模型,通常,在OpenGL中相机朝着−z⃗方向观察。
在这里,平移向量就是视点坐标,更准确的说是负的视点坐标,因为不得不对世界坐标系做相反的平移
