transform matrix阅读后的理解

1.首先很感谢博主的分享https://www.cnblogs.com/Ivy-s/p/6786622.html#4171054，然后我在这里记录一下自己的收获。

正文：

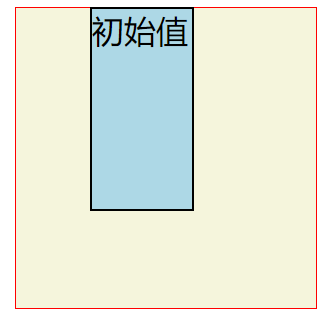
1）transform: matrix(1,0,0,1,0,0);//初始值

　　a:1  c:0  e:0　　　　x　　　　　1

　　b:0  d:1  f:0      ·     y　　=　　  1

　　   0     0    1　　　　1 　　　　   1

　　x`=ax+cy+e

　　y`=bx+dy+f

.contain{height: 300px;    width: 300px;border: 1px solid red;background-color: beige;margin: 50px auto;}
.mian{height: 100px;width: 50px;border: 1px solid black;background-color: lightblue;transform: matrix(1,0,0,1,0,0);//初始值}

2）transform: matrix(1,0,0,1,100,50);//X平移100,y平移50

3）transform: matrix(2,0,0,2,100,50);//平移后,X,y放大2倍

4）transform: matrix(0.2588,0.9659,-0.9659,0.2588,0,0);//旋转75度

　　matrix(cos75,sin75,-sin75,cos75,0,0)

　　cos75≈0.2588

　　sin75≈0.9659

　　a:cos75  c:-sin75  e:0　　　　x

　　b:sin75   d:cos75  f:0      ·        y

　　     0             0         1　　　　 1 

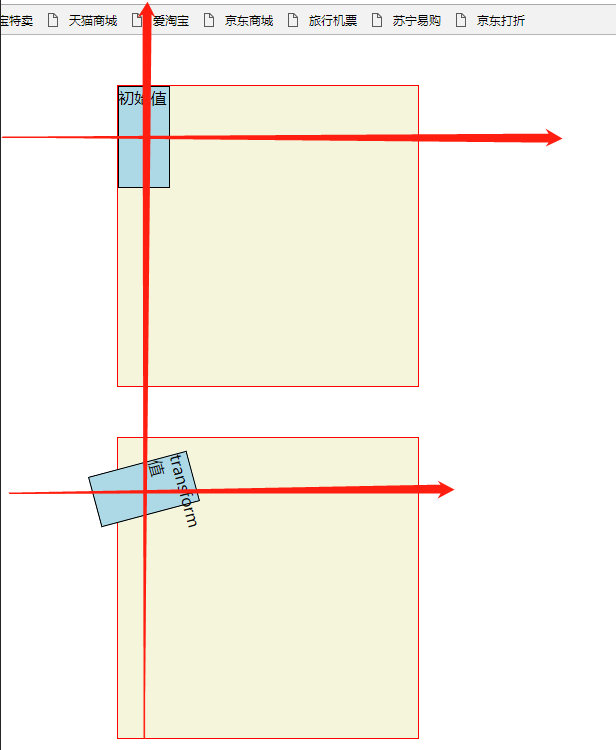
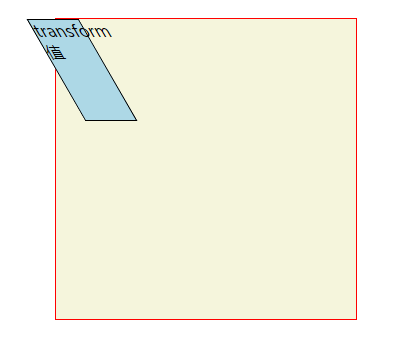
5)transform: matrix(1,0,0.577,1,0,0);//拉伸30度（X轴向前伸展，Y轴与图形右边线形成30度夹角）

matrix(1,tan(θy),tan(θx),1,0,0)

主要根据上文博主中提到的线代来计算

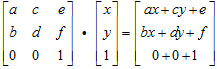
x'=ax+cy+e
y'=bx+dy+f