Room and Moor
Time Limit: 12000/6000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 263 Accepted Submission(s): 73
Problem Description
PM Room defines a sequence A = {A1, A2,..., AN}, each of which is either 0 or 1. In order to beat him, programmer Moor has to construct another sequence B = {B1, B2,... , BN} of the same length, which satisfies that:
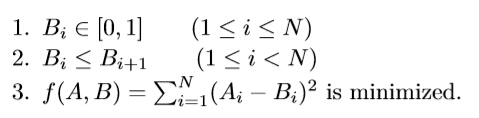
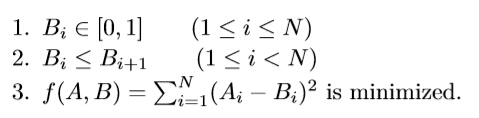
Input
The input consists of multiple test cases. The number of test cases T(T<=100) occurs in the first line of input.
For each test case:
The first line contains a single integer N (1<=N<=100000), which denotes the length of A and B.
The second line consists of N integers, where the ith denotes Ai.
For each test case:
The first line contains a single integer N (1<=N<=100000), which denotes the length of A and B.
The second line consists of N integers, where the ith denotes Ai.
Output
Output the minimal f (A, B) when B is optimal and round it to 6 decimals.
Sample Input
4
9
1 1 1 1 1 0 0 1 1
9
1 1 0 0 1 1 1 1 1
4
0 0 1 1
4
0 1 1 1
Sample Output
1.428571
1.000000
0.000000
0.000000
Source
Recommend
题意:很容易就读懂了。
题解:首先去掉前导零和最后的1,相当于把整个序列分成几个区间,每部分以1开头,0结尾,即如1 0 1 1 0 0等,可知对于每一个区间,要取得最小值,那这个部分所有的值即对应的这个区间内的平均数,如果这个平均数和前面一个区间的相比较大,就压入栈,否则将栈里的元素顶出,并与当前区间合并求平均数……知道比前面的大为止,最后求出每个区间的对应的Seg(ai - bi)^2 就可以了。至于为什么。。。。说实话全是YY,居然A掉了。。
AC代码如下:
1 #include <cstdio> 2 #include <cstring> 3 #include <stack> 4 using namespace std; 5 6 #define eps 0.00000001 7 const int LEN = 100010; 8 9 int arr[LEN]; 10 struct line 11 { 12 int l, r, sum; 13 double rate; 14 }; 15 16 stack<line> s; 17 18 int main() 19 { 20 int T, n; 21 line tmp; 22 scanf("%d", &T); 23 while(T--){ 24 scanf("%d", &n); 25 for(int i = 0; i < n; i++) 26 scanf("%d", arr+i); 27 int h = 0; 28 while(arr[h] == 0) 29 h++; 30 int k = n - 1; 31 while(arr[k] == 1) 32 k--; 33 for(int i = h; i <= k; i++){ 34 if (i == h || i > h && arr[i-1] == 0 && arr[i] == 1){ 35 tmp.l = i; 36 tmp.sum = 0; 37 } 38 if (i < k && arr[i] == 0 && arr[i+1] == 1 || i == k){ 39 tmp.r = i; 40 //printf("l = %d, r = %d ", tmp.l, tmp.r); 41 tmp.rate = tmp.sum * 1.0 / ((tmp.r - tmp.l + 1) * 1.0); 42 //printf("rate=%f ", tmp.rate); 43 while(true){ 44 if (s.empty() || s.top().rate - tmp.rate < eps){ 45 s.push(tmp); 46 break; 47 } 48 if (s.top().rate - tmp.rate > eps){ 49 tmp.l = s.top().l; 50 tmp.sum += s.top().sum; 51 tmp.rate = tmp.sum*1.0 / ((tmp.r - tmp.l + 1)*1.0); 52 s.pop(); 53 } 54 } 55 } 56 if (arr[i] == 1) 57 tmp.sum++; 58 } 59 double ans = 0; 60 while(!s.empty()){ 61 ans += ((1 - s.top().rate) * (1 - s.top().rate) * s.top().sum + s.top().rate * s.top().rate * (s.top().r - s.top().l + 1 - s.top().sum)); 62 s.pop(); 63 } 64 printf("%f ", ans); 65 } 66 return 0; 67 }