密码学

密码学

符号说明：

D(K,Y)     用密钥K和对称算法解密密文Y

D(PR_a,Y)     用A的私钥PR_a和非对称算法解密密文Y

D(PU_a,Y)     用A的公钥PR_a和非对称算法解密密文Y

E(K,X)     用密钥K和对称算法加密明文X

E(PR_a,,X)    用A的私钥和对称算法加密明文X

E(PU_a,X)    用A的公钥和对称算法加密明文X

K        密钥

PR_a        用户A的私钥

PU_a        用户A的公钥

C        密文

P        明文

gcb(a,b)    表示a和b的最大公因子

OSI安全框架

安全攻击:分为被动攻击和主动攻击。被动攻击包括非授权阅读消息、文件以及流量分析。主动攻击包括对消息或文件的篡改以及拒绝服务等。

安全机制：安全机制是一种处理过程（或实现该处理过程的设备），用来检测、阻止攻击或者从攻击状态恢复为正常状态。安全机制的例子有加密算法、数字签名和认证协议。

安全服务：安全服务包括认证、访问控制、数据保密性、数据完整性、非否认性以及可用性。

密码算法和协议的4个领域

对称加密：用于加密任意大小的数据块或数据流的内容，包括消息、文件、加密密钥和口令。

非对称加密：用于加密小的数据块，如加密密钥或数字签名中使用的Hash函数值。

数据完整性算法：用于保护数据块（例如一条消息）的内容免于修改。

认证协议：有许多基于密码算法的认证方案，用来认证实体的真实性。

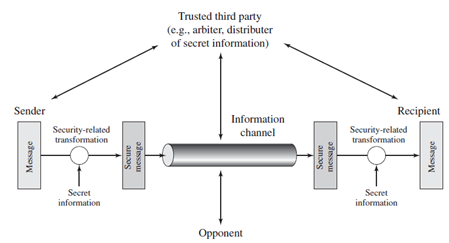
对称密码模型

对称加密方案有5个基本成分

明文：原始可理解的消息或数据，是算法的输入

加密算法：加密算法对明文进行各种代替和变换

密钥：密钥也是加密算法的输入。密钥独立于明文和算法。算法根据所用的特定密钥而产生不同的输出。算法所用的确切代替和变换也依靠密钥。

密文：作为算法的输出，看起来完全随机而杂乱的消息，依赖于明文和密钥。对于给定的消息，不同的密钥产生不同的密文，密文看上去是随机的数据流，并且其意义是不可理解的。

解密算法：本质上是加密算法的逆运算。输入密文和密钥，输出原始明文。

注：发送者和接收者必须在某种安全的形式下获得密钥并且必须保证密钥安全。如果有人发现该密钥，而且知道相应的算法，那么就能解读使用该密钥加密的所有通信。

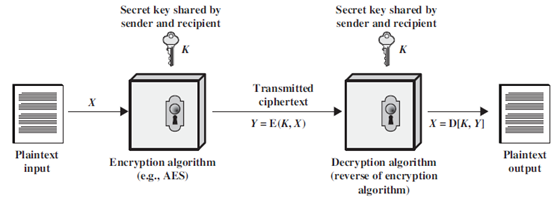
对称密码体制模型

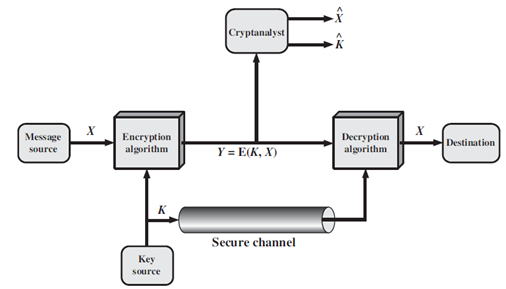
密码编码学系统具有的三个独立特征

替换明文为密文的运算类型：所有的加密算法都基于两个原理：替换和置换。代替是将明文中的每个元素（如位，字母，位组或字母组等）映射成另一个元素；置换是将明文中的元素重新排列。上述运算的基本要求是不允许有信息丢失（即所有的运算时可逆的）。大多数密码体制，也称为乘积密码系统，都使用多层代替和置换。

所用的密钥数：如果发送方和接收方使用相同的密钥，这种密码就称为对称密码、单密钥密码、秘密钥密码或传统密码。如果发收双方使用不同的密钥，这种密码就称为非对称密码、双钥或公钥密码。

处理明文的方法：分组密码每次处理输入的一组元素，相应的输出一组元素。流密码则是连续的处理输入元素，每次输出一个元素。

古典加密方法

代替技术

Caesar密码：对字母表中的每个字母，用它之后的第k个字母来代替。

加密算法：C = E(k,P) = (p+k) mod 26

解密算法：P = D(k,C) = (C-k) mod 26

单表代替密码: 对于Caesar密码允许任意代替。26个字母的任意置换，有26！的可能密钥。为每一条消息用一个字母表（给出从明文字母到密文字母的映射）加密。该加密很容易通过统计的方法进行破解，有两种主要的方法可以减少代替密码里明文结构在密文中的残留度：一种是对明文中的多个字母一起加密，另一种是采用多表代替密码。

Playfair密码：把明文中的双字母音节作为一个单元并将其转换成密文的"双字母音节"

Hill密码：该加密算法将m个连续的明文字母替换成m个密文字母，这是由m个线性方程决定，在方程中每个字母被指定为一个数值（a=0,b=1,….,z=25）。例如m=3，系统可以描述为：

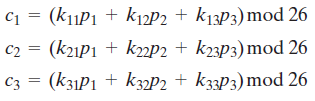
用行向量和矩阵表示如下：

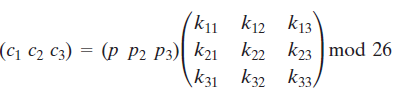
或

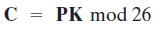
这里C和P是长度为3的行向量，分为代表密文和明文，K是一个3*3矩阵，代表加密密钥。运行按模26执行。

用一般术语，Hill密码系统可以表示如下：

同Playfair密码相比，Hill密码的有点是完全隐藏了单字母频率特性。实际上，Hill用的矩阵越大，所隐藏的频率信息就越多。因此，一个3*3的Hill密码不仅隐藏了单字母的频率性，还隐藏了双字母的频率性。虽然Hill密码足以抗唯密码攻击，但是容易被已知明文攻击破解。

多表代替加密：对简单单表代替的改进方法是在明文消息中采用不同的单表代替。这种方法一般称之为多表代替密码。所有这些方法都有以下的共同特征：1.采用相关的单表代替规则集。2.密钥决定给定变换的具体规则。

Vigenere密码：假设明文序列为

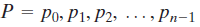
密钥序列

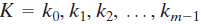
其中典型的是m<n，密码序列

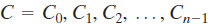
计算如下

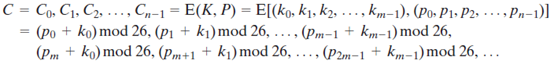
密钥第一个字母模26加到明文的第一个字母，接着是第二个字母，以此类推，直到前m个明文处理完毕。对于第二组的m个明文，重复使用密钥字母。继续该过程，直到所有的明文序列被加密完。加密过程的一般方程式是

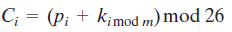
解密过程一般方程式

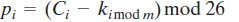
Vernam密码：提供了一种与明文毫无统计关系，且与它一样长的密钥。其运算基于二进制而非字母。该体制可以简明地表述为

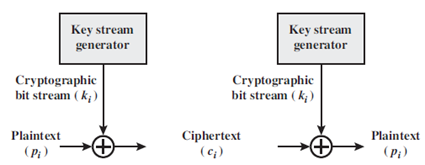
密文是通过对明文和密钥的逐位异或而成的。根据异或运算的性质，解密过程为

一次一密：一种对Vernam密码的改进方案，从而达到了最完善的安全性。使用与消息一样长且无重复的随机密钥来加密消息，另外，密钥只对一个消息进行加解密，之后丢弃不用。每一条消息都需要一个与其等长的新密钥。一次一密提供了完全的安全性，但是在实际中一次一密存在两个基本的难点：1.产生大规模随机密钥有实际困难。2.更令人担忧的是密钥的分配和保护。

置换技术：对明文进行置换，这种密码称为置换密码。最简单的例子是栅栏技术，按照对角线的顺序写出明文，而按行的顺序读出作为密文。一个更复杂的方案是把消息一行一行地写成矩形块，然后按列读出，但是把列的次序打乱。列的次序就是算法的密钥。

轮转机密码系统：轮转机的基本原理如下图所示，轮转机包括一组相互独立的旋转圆筒，电脉冲可以通过它。每个圆筒有26个输入引脚和26个输出引脚。内部连线使每一个输入仅同唯一一个输出连接。

 

隐写术：有两种方法可用来隐藏明文信息。隐写术，它可以隐藏信息的存在：而密码学则是通过对文本信息的不同转换而实现信息的对外不可读。

 

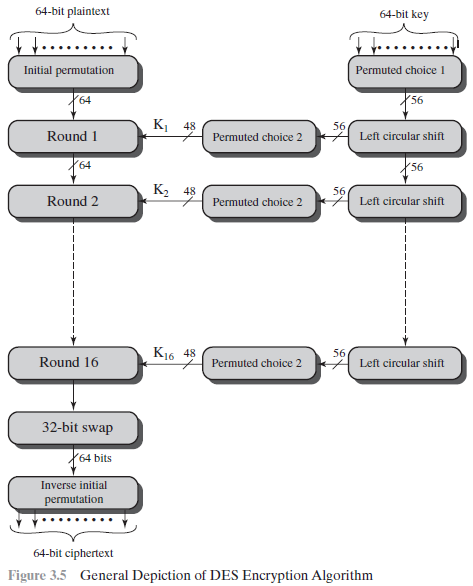
分组密码和数据加密标准

分组密码是一种加/解密方案，它将输入的明文分组当做一个整体处理，输出一个等长的密文分组。许多分组都采用Feistel结构，这样的结构由许多相同的轮函数组成。每一轮中，对输入数据的一半进行代替，接着用一个置换交换数据的两个等分部分。扩展初始的密钥使得每一轮中使用不同的子密钥。直到最近，DES一直是应用最为广泛的加密算法，它体现了经典的Feistel结构。DES使用64位的分组和56位的密钥。差分分析和线性分析是两种重要的密码分析方法。DES对这两种工具具有很强的免疫性。

DES (Data Encryption Standard): 数据加密标准

AES (Advanced Encryption Standard): 高级加密标准

流密码与分组密码：流密码每次加密数据流的一位或一个字节。古典流密码的例子有密钥自动生成的Vernam密码。位流必须以算法程序的方式实现，从而双方都可以生产具有密码学意义的位流。位流发生器是一个由密钥控制的算法，它必须产生在密码学意义上讲是强壮的位流。现在，两个只需要共享生成密钥，则各自可以生产密钥流。

    分组密码是将一个明文分组作为整体加密并且通常得到的是与明文等长的密文分组。典型的分组大小是64位或128位。同流密码一样，两个用户要共享一个对称加密密钥。

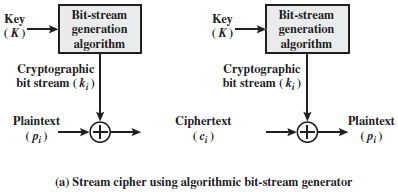
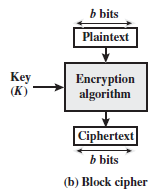
一般来说，分组密码的应用范围比流密码要广泛。绝大部分基于网络的对称密码应用使用的是分组密码。

Feistel密码结构的设计动机：分组密码作用于n位明文分组上，而产生n位密文分组。共有个不同的明文分组，且由于加密是可逆的（即可以解密），每一个明文分组将唯一对应一个密文分组。这样的变换称为可逆变换，或非奇异变换。所以，如果我们限定在可逆映射上，不同变换的总数是！个。从实现和运行的角度来看，采用大规模分组的任意可逆代替密码（即理想分组密码）是不可行的。因为对于这样的变换，映射本身就是密钥。本质上，它就是决定所有可能映射中某一个映射的密钥。一般地，对于n位的代替分组密码，密钥的规模是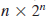。Feistel指出我们所需要的是对理想分组密码体制的一种近似体制而已。

Feistel密码：Feistel建议使用乘积密码的概念来逼近理想分组密码。乘积密码是指依次使用两个或两个以上的基本密码，所得结果的密码强度将强于所有单个密码的强度。这种方法的本质是开发一个分组密码，密钥长为k位，分组长为n位，采用个变换，而不是理想分组密码的！个可用变换。特别地，Feistel建议使用这样的密码:该种密码交替的使用代替和置换。代替和置换的定义如下：

代替：每个明文元素或元素组被唯一地替换为相应的密文元素或元素组。

置换：明文元素的序列被替换为该序列的一个置换。也就是说，序列中没有元素被添加，删除或替换，但序列中元素出现的顺序改变了。

混淆与扩散：扩散就是指使明文的统计特征消散在密文中，这可以通过让每个明文数字尽可能地影响多个密文数字获得，等价于说每个密文数字被许多明文数字影响。每一个分组密码都是明文分组到密文分组的变换，而这个变换又是依赖于密钥的。扩散的方法是尽可能地使明文和密文间的统计关系变得复杂，以挫败推到出密钥的企图。另一方面，混淆则是尽可能使密文和加密密钥之间的统计关系更加复杂以阻止攻击者发现密钥。

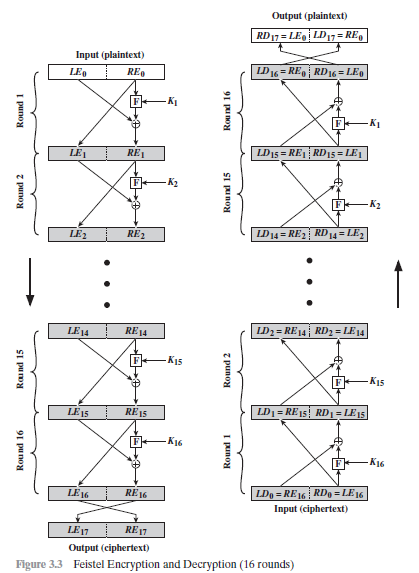
Feistel密码结构: 下图描述了Feistel结构，加密算法的输入是长为2w位的明文分组和密钥K。明文分组被分为等长的两部分：和。这两半数据经过n轮迭代后组合成密文分组。第i轮迭代的输入和来自于上轮迭代的输出；而输入的子密钥是由整个K推导出的。一般地，不同于K，也互不相同。每轮迭代都有相同的结构。代替作用在数据的左半部分。它通过用轮函数F作用于数据的右半部分后，与左半部分数据进行异或来完成。每轮迭代的轮函数是相同的，但是输入的子密钥是不同的。换一种说法，F是w位长的右半分组以及y位长的子密钥的函数，输出w位的值：F(,)。代替之后交换数据的左右两半完成置换。

Feistel解密算法：Feistel密码的解密过程本质上与加密过程一致。其规则如下:将密文作为算法的输入，但是逆序使用使用子密钥。也就是说第一轮使用,第二轮使用,直到最后一轮使用。这是一个很好的特点，因为我们不需要分别实现加密和解密两个算法。每轮的解密过程中间值与加密过程中间值左右互换的结果是相同的。第一轮的输入应等于加密过程第32轮输出左右不分互换的值。证明如下：

因此我们有=和=,所以解密过程的第一轮输出为||，正是加密过程第16轮输入左右部分互换的值。对于其他各轮也是如此。我们把它表示成一般形式。对于第i轮加密算法：

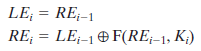
又可写为

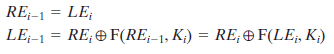
为了帮助说明前面的概念，看一个特别的例子并且关注加密的第15轮，对应于解密的第二轮。假设每一阶段的分组长度为32位（分为两个16位），密钥长度为24位。假设第14轮加密后的中间分组是DE7F03A6。那么=DE7F,=03A6。同时假设=12DE52。

 

 

数据加密标准：DES(Data Encryption Standard,DES) 数据加密标准。DES采用了64位的分组长度和56位密钥长度。它将64位的输入经过一系列变换得到64位输出。解密则使用了相同的步骤和相同的密钥。

DES加密：对于任意的加密方案，总有两个输入：明文和密钥。DES的明文长为64位，密钥长为56位。明文的处理经过了三个阶段。首先，64位的明文经过初始置换而重新排列。然后进行16轮相同函数的作用，每轮作用都有置换和代替。最后一轮迭代的输出有64位，它是输入明文和密钥的函数。其左半部分和右半部分互换产生预输出。最后预输出再被与初始置换互逆的置换产生64位的密文。除了初始和末尾的置换，DES的结构与Feistel密码的结构完全相同。右半部分给出了使用56位密钥的过程。首先，密钥经过一个置换后，再经过循环左移和一个置换分别得到各轮的子密钥用于各轮的迭代。每轮的置换函数都一样，但是由于密钥的循环移位使得各轮子密钥互不相同。

初始置换表：

 

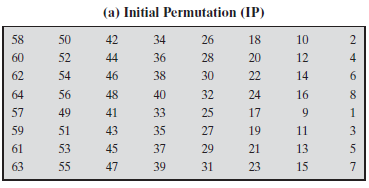
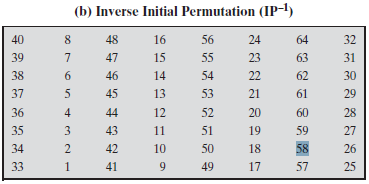
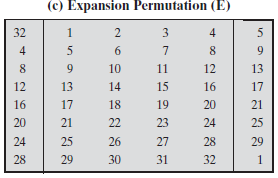
每轮变换的详细过程：64位数据的左右两个部分作为独立的32位数据，分别记为L和R。在经典的Feistel密码中，每轮变换的整个过程可以写为下面的公式：

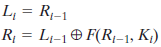
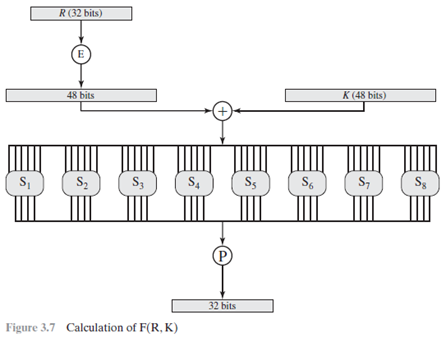
每一轮长48位，R是32位。首先将R用上图的扩展表c扩展为48位，其中有16位是重复的。这48位与异或，所得结果再用一个代替函数作用产生32位的输出，再用表d定义的置换进行作用后输出。

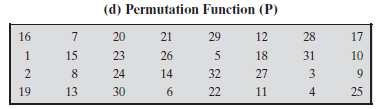
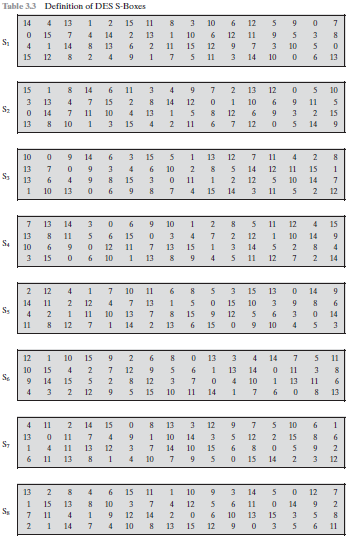
代替函数由8个S盒来组成，每个S盒都输入6位，输出4位。这些变换参见表3.3，其解释如下：盒输入的第一位和最后一位组成一个2进制数，用来选择S盒4行代替值中的一行，中间4位用来选择16列中的某一列。行列交叉处的十进制转化为二进制之后可得到4位二进制数。

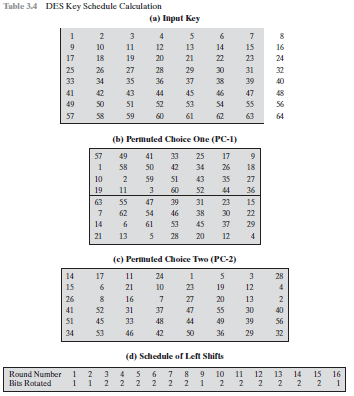
密钥的产生:算法输入64位密钥，密钥各位分别标记为1到64。如果表3.4a中没有阴影的部分，也就是每行的第8个位被忽略。首先用标志为置换选择1的表作用。所得56位密钥分别为两个28位数据和。每轮迭代中，和分别循环左移一位或两位，具体左移位数参见表3.4d。移位后的值作为下一轮的输入。它们同时也作为置换选择2的输入，将产生一个48位的输出作为函数F(,)的输入。

DES解密: Feistel密码的解密算法与加密算法是相同的，只是子密钥的使用次序相反。

雪崩效应：明文或密文的微小改变将对密文产生很大的影响，是任何加密算法需要的一个好性质。特别地，明文或密钥的某一位发生变化会导致密文的很多位发生变化。这被称为雪崩效应。如果相应的改变很小，可能会给分析者提供缩小搜索密钥或明文空间的渠道。

 

高级加密标准

要点：AES是一种分组密码，用以取代DES的商业应用。其分组长度为128位，密钥长度为128位、192位或256位。

AES未采用Feistel结构。每轮由4个单独的运算组成：字节代替，置换，有限域上的算术运算，以及与密钥的异或运算。

AES是一个对称分组密码算法，旨在取代DES成为广泛使用的标准。与公钥密码如RSA相对，AES以及大多数对称密码的结构都很复杂。

有限域算术：AES中的所有运算都是在8位的字节上进行的。特别地，加减乘除算术都是在有限域GF()上进行的。本质上，一个域就是一个集合，在该集合内，我们可以进行加减乘除运算，结果不离开集合。除法遵循规则a/b=a()。一个有限域（具有有限个元素）的例子是集合，其中p是一个素数，且其内的运算时模p进行的。

所有的加密算法，包括对称的和非对称的，都用到了整数的算术运算。如果算法用到了除法，我们需要用到定义在域上的算术。这是因为除法需要没有给非零元素有一个乘法逆元。出于习惯和实现的效率考虑，给定整数的位数，我们希望使用具有该位长度的所有整数，而不浪费一些位模式。即我们希望使用0到内的所有整数，其刚好是一个n位的字。遗憾的是这些整数的集合在模算术下并不是一个域。例如，整数2在内没有乘法逆元。也就是说不存在b使得2b mod 。有一种方法可以定义含有个元素的有限域，该域被称为GF()。考虑所有次数小于等于n-1，系数为0,1的多项集合S。因此，每一个多项式具有如下形式：

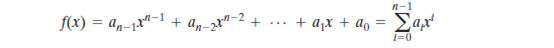
其中每个取值0或1，集合S内共有个元素。对于n=3，集合内的8个多项式为

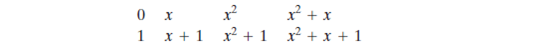
定义合适的算术运算，则每一个这样的集合S都是一个有限域。定义由如下各项组成。

1. 该运算遵循嗲书基本规则中的普通多项式运算规则及如下两条限制
2. 系数运算以2为模，这和XOR是一样的
3. 如果乘法运算的结果是次数大于n-1的多项式，那么必须用某个次数为n的不可约多项式m(x)进行约化，即用m(x)去除并取余式。对于多项式f(x)，这个余数可表示为r(x)=f(x) mod m(x)。一个多项式m(x)称为不可约多项式，当且仅当该多项式不能标识为次数小于m(x)的次数的两个多项式的乘积。

例如，为了构造GF(),我们需要选择次数为3的不可约多项式。加法等价于各项的对位异或。GF()内的一个多项式可以由它的二元系数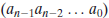唯一表示。因此，GF()内的每个多项式可以由n位的数来表示。加法由两个n位的数进行对位异或来实现。对于乘法，GF()内的数乘以2可以先左移，然后根据条件异或上一个常数。乘上一个大数可以重复运用该规则。总结一下，AES在8位的字节上运算。两个字节的加定义为对位异或操作。两个字节的乘定义为有限域GF()内的乘法，其中不可约多项式为

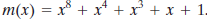
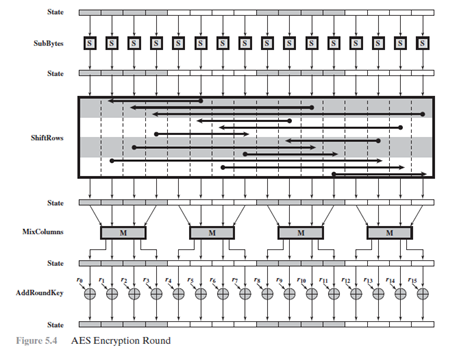
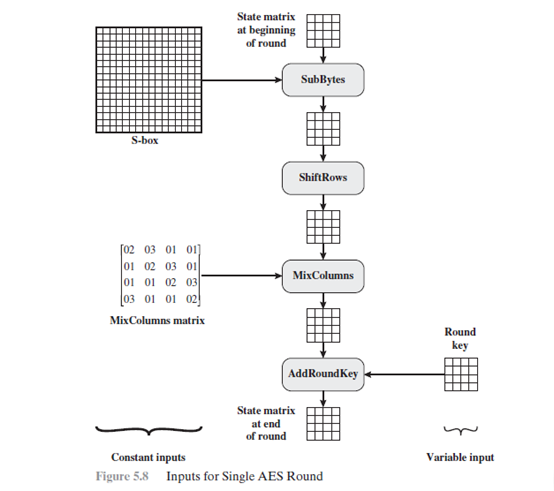
AES总体结构：明文分组的长度为128位即16字节，密钥长度可以为16，24或32字节（128，192或256位）。根据密钥的长度，算法被称为AES-128,AES-192,AES-256。加密和解密算法的输入是一个128位分组。这个分组被复制到state数组，并在加密或解密的各个阶段被修改。图5.2（a）描述了这些操作。

同样的密钥也被描述为字节的方阵。这个密钥接着被扩展为密钥字阵列。图5.2（b）展示了128位密钥的扩展。每个字是4个字节，128位密钥最终扩展为44字序列。

矩阵中字节是按照列进行排序的。所以，加密算法的128位明文分组输入的前4个字节被按顺序放在了in矩阵的第一列，接着4个字节放在了第二列，等等。相似地，扩展密钥的前四个字节（形成了一个字）被放在w矩阵的第一列。

密码由N轮组成，其中轮数依赖于密钥长度：16字节密钥是10轮，24字节密钥对应12轮，32节密钥对应14轮。前N-1轮由4个不同的变换组成：字节代替、行移位、列混淆和轮密钥加密。最后一轮仅包含桑变换，而在第一轮的前面有一个起始地单变换（轮密钥加），可以视为0轮。每一轮变换输入一个或多个，并输出一个的矩阵。图5.1说明每轮的输出是一个的矩阵，最后一轮的输出为密文。同样，密钥扩展函数产生N+1轮密钥，它们是互不相同的矩阵。每一轮密钥作为每轮的的轮密钥加变换的一种输入。

 

 

 

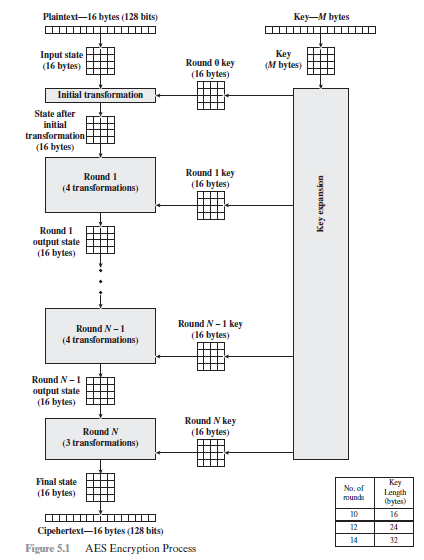
图5.3更加详细地展示了AES密码，指明了每轮的变换顺序，并展示了相应的解密函数。

1. AES结构的一个显著特征是它不是Feistel结构。在经典的Feistel结构，数据分组中的一半被用来修改数据分组中的另一半，然后交换这两部分。AES算法未使用Feistel结构，而是在每一轮都使用代替和混淆将整个数据分组作为一个单一的矩阵处理。
2. 输入的密钥被扩展成由44个32位字所组成的数组w[i]。从图5.3中可以看出，每轮有四个不同的字（128位）作为该轮的轮密钥。
3. 由四个不同的阶段组成，包括一个置换和三个代替：
   字节代替：用一个S盒完成分组的字节到字节的代替。

   行移位：一个简单的置换

   列混淆：利用域GF()上的算术特征的一个代替

   轮密钥加：当前分组和扩展密钥的一部分进行按位XOR

4. 算法结构非常简单。对加密解密操作，算法又轮密钥加开始，接着执行9轮迭代运算，每轮都包含所有4个阶段的代替，接着是第10轮的三个阶段。
5. 仅仅在轮密钥加阶段中使用密。由于这个原因，该算法以轮密钥加开始，以轮密要加结束。如果将其他不需要密钥的运算用于算法开始或结束的阶段，在不知道密钥的情况下就能计算其逆，故不能增加算法的安全性。
6. 轮密钥加实质上是一种Vernam密码形式，就其本身是不是不难破译的。而另外三个阶段一起提供了混淆，扩散以及非线性共嗯那个。因这些阶段没有涉及密钥，故就它们自身而言，并未提供算法的安全性。我们可把该算法视为一个分组的XOR加密（轮密钥加），接着对这个分组混淆（其他的三个阶段），再接着又是XOR加密，如此交替执行。这种方式非常有效且非常安全。
7. 每个阶段均可逆。对字节代替、行移位和列混淆，在解密算法中用与它们对应的逆函数。轮密钥加的逆就是用同样的轮密钥和分组相异或，其原理就是。
8. 同大多数分组密码一样，解密算法按逆序方式利用了扩展密钥。然而，AES的解密算法和加密算法并不一样。这是由AES的特定结构所决定的。
9. 一旦将所有的四个阶段求逆，很容易证明解密函数的确可以恢复原来的明文。图5.3中加密和解密流程在纵向上是相反的。在每个水平点上（如图中由破折号组成的线），state数组在加密和解密函数中是一样的。
10. 加密和解密过程的最后一轮均只包含三个阶段。这是由AES的结构所决定的，而且也是密码算法可逆性所要求的。

 

 

AES的变换函数

字节代替变换:正向和逆向变换。被称为字节代替的正向字节代替变换是一个简单的查表操作。AES定义了一个S盒，它是由个字节组成的矩阵，包含了8位所能表示的256个数的一个置换。state中每个字节按照如下的方式映射为一个新的字节：把该字节的高4位作为行值，低4位作为列值，以这些行列值作为索引从S盒的对应位置取出元素作为输出。例如，十六进制数{95}所对应的S盒的行值是9，列值是5，S盒中在此位置的值是{2A}。相应地{95}被映射为{2A}。

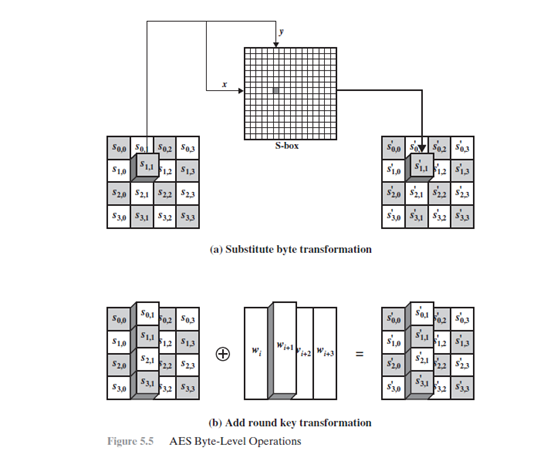
行移位变换：下图描述了正向行一位变换stage的第一行保持不变。把state的第二行循环左移一个字节state的第三行循环左移两个字节。state的第四行循环左移三个字节。行移位变换的一个例子如下：

逆向行移位变换将state中的后三行执行相反方向的移位操作，如第二行向右循环移一个字节，其他行类似。

列混淆变换：列混淆变换的正向列混淆变换对每列独立进行操作。每列中的每个字节被映射为一个新值，此值由该列中的4个字节通过函数变换得到。这个变换可由下面基于state的矩阵乘法表示：

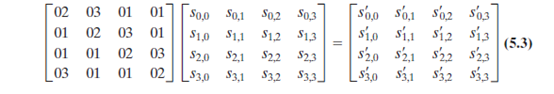
轮密钥加变换：正向的和逆向变换。在轮密钥加变换中，128位的state按位与128位的轮密要XOR。如图5.5（b）所示，该操作可以视为state的一列中四个字节与轮密钥的一个字进行列间的操作：我们也能将其视为字节级别的操作。

例子中第一个矩阵式state，第二个矩阵是轮密钥。逆向轮密钥加变换是和正向轮密钥加变换一样的，因为异或操作是其本身的逆。

基本原理:轮密钥加变换非常简单，却能影响state中的每一位。密钥扩展的复杂性和AES的其他阶段运算的复杂性，确保了该算法的安全性。

AES的密钥扩展

密钥扩展算法：AES密钥扩展算法的输入值是4个字(16字节)，输出是一个由44个字组成（176字节）的一维线性数组。这足以为初始轮密钥加阶段和算法中其他10轮中的每一轮提供4字的轮密钥。

对w数组中下标为4的倍数的元素采用了更复杂的函数来计算。图5.9阐明了如何计算扩展密钥，其中使用符号g来表示这个复杂函数。函数g由下述子功能组成：

1. 字循环的功能是使一个字中的4个字节循环左移一个字节，即将输入字[]
2. 字代替利用S盒对输入字中的每个字节进行字节代替
3. 步骤1和步骤2的结果再与轮常量Rcon[j]相异或。

基本原理：Rinddael的开发者设计了密钥扩展算法来防止已有的密码分析攻击。使用与轮相关的轮常量是为防止不同轮的密钥产生方式上的对称性或相似性。

1. 知道密钥或轮密钥的部分位不能计算出轮密钥的其他位。
2. 它是一个可逆的变换[即知道扩展密钥中任何连续的Nk个子能够重新产生整个扩展密钥(Nk是构成密钥所需的字数)]
3. 能够在各种处理器上有效地执行。
4. 使用轮常量来消除对称性。
5. 将密钥的差异性扩散到轮密钥中的能力；即密钥的每个位能影响到轮密钥的许多位。
6. 足够的非线性以防止轮密钥的差异完全由密钥的差异所决定。
7. 易于描述。

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

附相关数学知识

置换

 

有限元素的集合S的置换是S的所有元素的有序排列，且每个元素只出现一次。例如，如果S={a,b,c}，则S有6个置换：

abc acb bac bca cab cba

一般具有n个元素的集合有n!个置换

数论

分数mod：

1.找到一个整数P使得1/m+p=(1+p*m)/m,使得整数（1+p*m）是n的倍数，也即（1+p*m）mod n=0。

2.问题转化为1/m ≡ -p mod n,此时只要求得 –p mod n 的值就可以了。

例:

1/3 mod 7= ?; 1/3+2=7/3; -2 mod 7=5, 也就是1/3 mod 7= 5;

如果(a mod n)=(b mod n) 则我们称整数a 和 b 是模n同余的。可以表示为a≡b (mod n)

 

 

修改的Euclid算法：

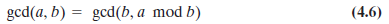
扩展的Euclidd算法：

一般的可以证明对于两个给定的整数a和b，ax+by的最小整数等于gcd(a,b)

扩展Euclid算法去计算(x,y,d)

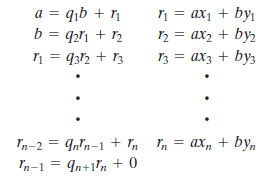
现在可以通过移项得到

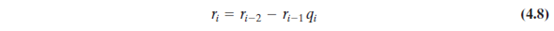
同样，从i-1和i-2行，可得到值

代入式（4.8）

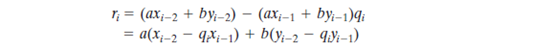
然而，我们已经假设

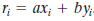
因此

总结计算过程如下:

 

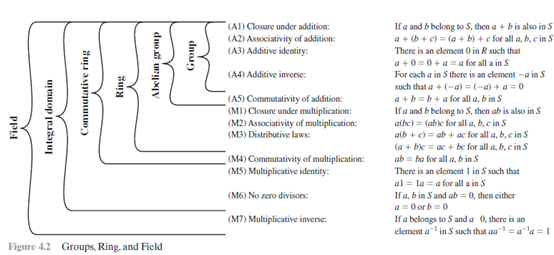
群、环和域

群：群G，有时记为{ G , ∙ }，是定义了一个二元运算的集合，这个二元运算可表示为 ∙ ，G中每一个序偶(a,b)通过运算生成G中的元素（a ∙ b），并满足一下公理：
(A1)封闭性：如果a和b都属于G，则a ∙ b也属于G。

(A2)结合律：对于G中任意元素a,b,c,都有a ∙ ( b ∙ c ) = ( a ∙ b ) ∙ c

(A3)单位元：G中存在一个元素e,对于G中任意元素a，都有a ∙ e = e ∙ a = a成立

(A4)逆元：对于G中任意元素a,G中都存在一个元素，使得下式成立：

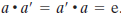
如果一个群的元素是有限的，则该群称为有限群，并且群的阶就等于群众元素的个数。否则称该群为无限群。

一个群如果还满足一下条件，则称为交换群：

(A5)交换律：对于G中任意的元素a,b,都有a ∙ b = b ∙ a

循环群:我们在群中定义求幂运算为重复运用群众的运算，如。而且我们定义作为单位元；并且，其中是a在群内的逆元素。如果群G中的每一个元素都是一个固定元素a(aG)的幂（k为整数），则称群G是循环群。我们认为元素a生成了群G，或者说a是群G的生成元。循环群总是交换群，它可能是有限群或无限群。

eg：整数的加法群是一个无限循环群，它由1生成。在这种情况下，幂被解释为用加法合成的，因此n是1的n次幂。

环: 环R，有时记为{R,,},是一个有两个二元运算的集合，这两个二元运算分别称为加法和乘法，且对于R中的任意元素a,b,c满足以下公理。

(A1~A5)R关于加法是一个交换群；也就说，R满足从A1到A5的所有原则。对于此种情况下的加法群我们用0表示其单位元，-a表示a的逆元。

(M1)乘法的封闭性：如果a和b都属于R，则ab也属于R。

(M2)乘法的结合律：对于R中的任意元素a,b,c,有a(bc)=(ab)c成立。

(M3)分配律：对于R中的任意元素a,b,c,下面两个式子总成立：

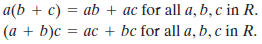
本质上说，环就是一个集合，我们可以在其上进行加法，减法和乘法而不脱离该集合。实数上所有n阶方阵的集合关于加法和乘法构成一个环。

环如果满足以下条件，则称为交换环。

(M4)乘法的交换律：对于R中任意元素a,b,有ab=ba成立。

完整环是满足以下公理的交换环：

(M5)乘法单位元：在R中存在元素1，使得对于R中的任意元素a，有a1=1a=a成立。

(M6)无零因子：如果有R中有元素a,b,且ab=0，则必有a=0或b=0。

将普通加法和乘法运算下的整数集合（包括整数、负数和0）记为S，则S是一个整环。

域：域F，有时记为{F,,},是有两个二元运算的集合，这两个二元运算分别称为加法和乘法，且对于F中的元素a,b,c满足以下公里：

(A1-M6)

(M7)乘法逆元：对于F中的任意元素a（除0以外），F中都存在一个元素使得下式成立：

=1

本质上说，域就是一个集合，我们可以在其上进行加法，减法，乘法和除法而不脱离该集合。除法又按以下规则来定义：

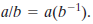
有理数集合，实数集合以及复数集合都是我们熟悉的域的例子。需要指出的是，所有整数的集合并不是一个域，因为并不是集合中所有的元素都有乘法逆元；实际上，整数集合中只有元素1和-1有乘法逆元。

 

有限域GF(p)

阶为的有限域一般记为GF() , GF代表Galois域，以第一位研究有限域的数学家的名子命名。

阶为P的有限域：给定一个素数p，元素个数为p的有限域GF(p)被定义为整数{0,1,…,p-1}的集合,其运算为模p的算术运算。

若n为素数，中所有的非零整数都与n互素，因此中所有非零整数都有乘法逆元。

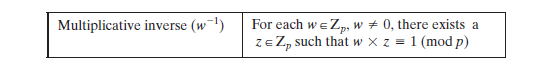
因为w和p互素，如果我们用w乘以的所有元素，得出的剩余类是中所有元素的另一种排列。因此，恰好只有一个剩余类值为1。因而，中有这样的整数，当它乘以w，得余数1。这个整数就是w的乘法逆元，记为,所以其实是一个有限域。

在GF(p)中求乘法逆元:如果a和b互素，则b有模a的乘法逆元。也就是说，如果gcd(a,b)=1，那么b有模a的乘法逆元。即对于正整数b<a,存在<a使。如果a是素数并且b<a，则显然a和b互素，且其最大公因子为1。运用扩展的Euclid算法很容易计算。

扩展Euclid算法如下：

现在，如果gcd(a,b)=1，自由ax+by=1。我们有如下式子

然而，如果by mod a =1，则y=。因此如果gcd(a,b)=1，则通过Euclid算法可以获得b的乘法逆元。更一般地，对于任意的n，扩展Euclid算法可以用于求取内的乘法逆元。如果运用扩展Euclid算法于方程nx+by=d,并且得到d=1,则。

多项式运算：只讨论单变元多项式，且可把多项式运算分为三种。

使用代数基本规则的普通多项式运算。

系数运算是模P运算的多项式运算，即系数在GF(p)中。

系数在GF(p)中，且多项式被定义为模一个n次多项式m(x)的多项式运算。

系数在中的多项式运算：多项式的系数是域F的元素。我们称其为域F上的多项式。这种情况下，容易看出这样的多项式集合是一个环，称为多项式环。也就是说，如果我们把每个不同的多项式视为集合中的元素，这个集合就是一个环。

有限域GF():在有限域中不会用模算术，因为那样不能构成域。将使用多项式算术来构造我们需要的域。

多项式模运算：设集合S由域上次数小于等于n-1的所有多项式组成。每一个多项式具有如下形式：

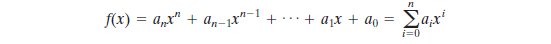
其中，在集合{0,1,…..,p-1}上取值。S中共有个不同的多项式。

如果定义了合适的运算，那么没有给这样的集合S都是一个有限域。定义由如下几条组成：

该运算遵循代数基本规则中的普通多项式运算规则及如下两条限制。

系数运算以P为模，即遵循有限域上的运算规则。

如果乘法运算的结果是次数大于n-1的多项式，那么必须将其除以某个次数为n的即约多项式m(x)并取余式。对于多项式f(x)，这个余数可表示为r(x)=f(x) mod m(x)。

和简答模运算类似，多项式模运算也有剩余类集合的概念。设m(x)为n次多项式，则模m(x)剩余类集合有个元素，其中每个元素都可以表示成一个m次多项式(m<n)

以m(x)为模的剩余类[x+1]由所有满足a(x)≡(x+1) (mod m(x))的多项式a(x)组成。也就是说，剩余类[x+1]中的所有多项式a(x)满足等式a(x) mod m(x) = x+1。

求乘法逆元：扩展Euclid算法则可以用来求一个多项式的乘法逆元。

加法：多项式加法是将相应的系数分别相加，而对于上的多项式，加法其实就是异或（XOR）运算。所以，GF()中的两个多项式加法等同于按位异或运算。

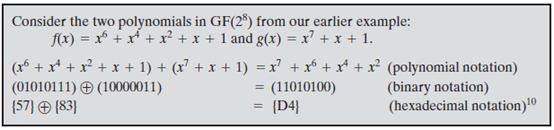
乘法：一般地，在GF()上对于n次多项式P(x)，有。

生成元：阶为q的有限域F的生成元是一个元素，记为g，该元素的前q-1个幂构成了F的所有非零元素，即域F的元素为0，,,,…..,。考虑由多项式f(x)定义的域F，如果F内的一个元素b满足f(b)=0，则称b为多项式f(x)的根。最后，可以证明一个不可约多项式的根g是这个不可约多项式定义的有限域的生成元。