Leetcode 304.二维区域和检索-矩阵不可变

二维区域和检索 - 矩阵不可变

给定一个二维矩阵，计算其子矩形范围内元素的总和，该子矩阵的左上角为 (row1, col1) ，右下角为 (row2, col2)。

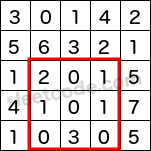
上图子矩阵左上角 (row1, col1) = (2, 1) ，右下角(row2, col2) = (4, 3)，该子矩形内元素的总和为 8。

示例:

给定 matrix = [

[3, 0, 1, 4, 2],

[5, 6, 3, 2, 1],

[1, 2, 0, 1, 5],

[4, 1, 0, 1, 7],

[1, 0, 3, 0, 5]

]

 

sumRegion(2, 1, 4, 3) -> 8

sumRegion(1, 1, 2, 2) -> 11

sumRegion(1, 2, 2, 4) -> 12

说明:

1. 你可以假设矩阵不可变。
2. 会多次调用 sumRegion 方法。
3. 你可以假设 row1 ≤ row2 且 col1 ≤ col2。

Approach #4 (Caching Smarter) [Accepted]

Algorithm

We used a cumulative sum array in the 1D version. We notice that the cumulative sum is computed with respect to the origin at index 0. Extending this analogy to the 2D case, we could pre-compute a cumulative region sum with respect to the origin at (0,0)(0, 0)(0,0).

Sum(OD) is the cumulative region sum with respect to the origin at (0, 0).

How do we derive Sum(ABCD)Sum(ABCD)Sum(ABCD) using the pre-computed cumulative region sum?

Sum(OB) is the cumulative region sum on top of the rectangle.

Sum(OC) is the cumulative region sum to the left of the rectangle.

Sum(OA) is the cumulative region sum to the top left corner of the rectangle.

Note that the region Sum(OA)Sum(OA)Sum(OA) is covered twice by both Sum(OB)Sum(OB)Sum(OB) and Sum(OC)Sum(OC)Sum(OC). We could use the principle of inclusion-exclusion to calculate Sum(ABCD)Sum(ABCD)Sum(ABCD) as following:

Sum(ABCD)=Sum(OD)−Sum(OB)−Sum(OC)+Sum(OA) Sum(ABCD) = Sum(OD) - Sum(OB) - Sum(OC) + Sum(OA) Sum(ABCD)=Sum(OD)−Sum(OB)−Sum(OC)+Sum(OA)

class NumMatrix {

    private int[][] dp;

    public NumMatrix(int[][] matrix) {
        if (matrix.length == 0 || matrix[0].length == 0) return;
        dp = new int[matrix.length + 1][matrix[0].length + 1];
        for (int r = 0; r < matrix.length; r++) {
            for (int c = 0; c < matrix[0].length; c++) {
                dp[r + 1][c + 1] = dp[r + 1][c] + dp[r][c + 1] + matrix[r][c] - dp[r][c];
            }
        }
    }

    public int sumRegion(int row1, int col1, int row2, int col2) {
        return dp[row2 + 1][col2 + 1] - dp[row1][col2 + 1] - dp[row2 + 1][col1] + dp[row1][col1];
    }


}

/**
 * Your NumMatrix object will be instantiated and called as such:
 * NumMatrix obj = new NumMatrix(matrix);
 * int param_1 = obj.sumRegion(row1,col1,row2,col2);
 */