同进化算法(进化算法是受生物进化机制启发而产生的一系列算法)和人工神经网络算法(神经网络是从信息处理角度对人脑的神经元网络系统进行了模拟的相关算法)一样,群智能优化算法也属于一种生物启发式方法,它们三者可以称为是人工智能领域的三驾马车(实际上除了上述三种算法还有一些智能算法应用也很广泛,比如模拟金属物质热力学退火过程的模拟退火算法(Simulated Algorithm,简称SA),模拟人体免疫系统在抗原刺激下产生抗体过程的人工免疫系统算法(Artificial Immune System,简称AIS)等,但是相对三者而言,模拟退火算法和人工免疫系统算法已逐渐处于低潮期)。群智能优化算法主要是模拟了昆虫,兽群、鸟群和鱼群的群集行为,这些群体按照一种合作的方式寻找食物,群体中的每个成员通过学习它自身的经验和其他成员的经验来不断地改变搜索的方向。群体智能优化算法的突出特点就是利用了种群的群体智慧进行协同搜索,从而在解空间内找到最优解。
常见的群体智能优化算法主要有如下几类:
蚁群算法(Ant Colony Optimizatio,简称ACO)【1992年提出】;
粒子群优化算法(Particle Swarm Optimization,简称PSO)【1995年提出】
菌群优化算法(Bacterial Foraging Optimization,简称BFO)【2002年提出】
蛙跳算法(Shuffled Frog Leading Algorithm,简称SFLA)【2003年提出】
人工蜂群算法(Artificial Bee Colony Algorithm,简称ABC)【2005年提出】
除了上述几种常见的群体智能算法以外,还有一些并不是广泛应用的群体智能算法,比如萤火虫算法,布谷鸟算法,蝙蝠算法以及磷虾群算法等等。
蚁群算法
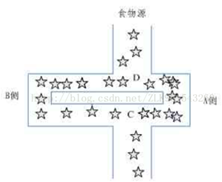
蚂蚁寻找食物的过程
单只蚂蚁的行为及其简单,行为数量在10种以内,但成千上万只蚂蚁组成的蚁群却能拥有巨大的智慧,这离不开它们信息传递的方式———信息素。
蚂蚁在行走过程中会释放一种称为"信息素"的物质,用来标识自己的行走路径。在寻找食物的过程中,根据信息素的浓度选择行走的方向,并最终到达食物所在的地方。
信息素会随着时间的推移而逐渐挥发。
在一开始的时候,由于地面上没有信息素,因此蚂蚁们的行走路劲是随机的。蚂蚁们在行走的过程中会不断释放信息素,标识自己的行走路径。随着时间的推移,有若干只蚂蚁找到了食物,此时便存在若干条从洞穴到食物的路径。由于蚂蚁的行为轨迹是随机分布的,因此在单位时间内,短路径上的蚂蚁数量比长路径上的蚂蚁数量要多,从而蚂蚁留下的信息素浓度也就越高。这为后面的蚂蚁们提供了强有力的方向指引,越来越多的蚂蚁聚集到最短的路径上去。
什么是蚁群算法
蚁群算法就是模拟蚂蚁寻找食物的过程,它能够求出从原点出发,经过若干个给定的需求点,最终返回原点的最短路径。这也就是著名的旅行商问题(Traveling Saleman Problem, TSP)。
蚁群算法规则
觅食规则
蚂蚁感知范围是一个3*3的格子,也就是说,他这个格子有食物就直接过去
移动规则
蚂蚁会朝着信息素浓的地方移动,如果没有感知到信息素,就会按着惯性一直走下去,别忘了蚂蚁会创新。
避障规则
蚂蚁在遇到障碍物的时候会选择随机方向移动,同时遵循上面两个规则。
信息素规则
蚂蚁在刚发现食物的时候挥洒的信息素越多,距离越远,信息素越少。
import os,sys,random from math import * import pylab as pl import pandas as pd BestTour=[] #用于放置最佳路径选择城市的顺序 CitySet=set() #sets数据类型是无序的,没有重复元素的集合,两个sets之间可以做差集,即第一个集合中移除第二个集合中也存在的元素 CityList=[] #城市列表即存放代表城市的序号 PheromoneTraiList=[] #信息素列表(矩阵) PheromoneDeltaTraiList=[] #释放信息素列表(矩阵) CityDistanceList=[] #两两城市距离列表(矩阵) AntList=[] #蚂蚁列表 class BACA:#定义类BACA,执行蚁群算法 def __init__(self,citycount=51,antCount=51,q=80,alpha=1,beta=3,rou=0.4,nMax=300): #初始化方法,antCount为蚂蚁数,nMax为迭代次数 self.CityCount=citycount #城市数量 self.AnCount=antCount #蚂蚁数量 self.Q=q #信息素增加强度系数 self.Alpha=alpha #表征信息素重要程度的参数 self.Beta=beta #表征启发因子重要程度的参数 self.Rou=rou #信息素蒸发系数 self.Nmax=nMax #最大迭代次数 self.Shortest=10e6 #初始化最短距离应该尽可能大,至少大于估算的最大城市旅行距离 pl.show() random.seed() #设置随机种子 #初始化全局数据结构及值 for nCity in range(self.CityCount):#循环城市总数的次数 BestTour.append(0)#设置最佳路径初始值均为0 for row in range(self.CityCount): pheromoneList=[] #定义空的信息素列表 pheromoneDeltaList=[] #定义空的信息素列表 for col in range(self.CityCount): pheromoneList.append(100) #定义一个城市到所有城市信息素的初始值 pheromoneDeltaList.append(0) #定义一个城市到所有城市释放信息素的初始值 PheromoneTraiList.append(pheromoneList) #建立每个城市到所有城市路径信息素的初始值列表 PheromoneDeltaTraiList.append(pheromoneDeltaList) #建立每个城市到所有城市路径释放信息素的初始值列表矩阵 def ReadCityInfo(self,fileName): file=open(fileName) for line in file.readlines(): cityN,cityX,cityY=line.split() CitySet.add(int(cityN)) CityList.append((int(cityN),float(cityX),float(cityY))) for row in range(self.CityCount): distanceList=[] #建立临时存储距离的空列表 for col in range(self.CityCount): #计算每个城市到所有城市的距离值 distance=sqrt(pow(CityList[row][1]-CityList[col][1],2)+pow(CityList[row][2]-CityList[col][2],2)) distance=round(distance) distanceList.append(distance) #追加一个城市到所有城市的距离值 CityDistanceList.append(distanceList) #追加一个城市到所有城市的距离值,为矩阵,即包含子列表 file.close() def PutAnts(self): #定义蚂蚁所选择城市以及将城市作为参数定义蚂蚁的方法和属性 AntList.clear() for antNum in range(self.AnCount): city=random.randint(1,self.CityCount) ant=ANT(city) #蚂蚁类ANT的实例化,即将每只蚂蚁随机选择的城市作为传入的参数,使之具有ANT蚂蚁类的方法和属性 AntList.append(ant) #将定义的每只蚂蚁追加到列表中 def Search(self): #定义搜索最佳旅行路径方法的主程序 for iter in range(self.Nmax): self.PutAnts() for ant in AntList: for ttt in range(len(CityList)): #执行蚂蚁ant.MoveToNextCity()方法,获取蚂蚁每次旅行时的旅行路径长度Currlen,禁忌城市列表TabuCityLsit等属性值 ant.MoveToNextCity(self.Alpha,self.Beta) ant.two_opt_search() ant.UpdatePathLen() tmpLen=AntList[0].CurrLen #将蚂蚁列表中第一只蚂蚁的旅行路径长度赋值给新的变量tmpLen tmpTour=AntList[0].TabuCityList #将获取的蚂蚁列表的第一只蚂蚁的禁忌城市列表赋值给新的变量tmpTour for ant in AntList[1:]: #循环遍历蚂蚁列表,从索引值1开始,除第一只外 if ant.CurrLen < tmpLen: tmpLen=ant.CurrLen tmpTour=ant.TabuCityList if tmpLen < self.Shortest: self.Shortest=tmpLen BestTour = tmpTour print(iter,":",self.Shortest,":",BestTour) pl.clf() x = []; y = [] for city in BestTour: x.append(CityList[city - 1][1]) y.append(CityList[city - 1][2]) x.append(x[0]) y.append(y[0]) pl.plot(x, y) pl.scatter(x, y, s=30, c='r') pl.pause(0.01) self.UpdatePheromoneTrail() def UpdatePheromoneTrail(self): #定义更新信息素的方法 for ant in AntList: for city in ant.TabuCityList[0:-1]: idx=ant.TabuCityList.index(city) #获取当前循环,禁忌城市的索引值 nextCity=ant.TabuCityList[idx+1] PheromoneDeltaTraiList[city-1][nextCity-1]+=self.Q/ant.CurrLen #逐次更新释放信息索列表,注意矩阵行列索代表的意义,[city-1]为选取的子列表即当前城市与所有城市间路劲的 #的释放信息素值,初始值均为0,[nextCity-1]为在子列表中对应紧邻的下一个城市,释放信息素为Q,信息素增加强度 #系数与蚂蚁当前旅行路径长度CurrLen的比值,路径长度越小释放信息素越大,反之则越小。 PheromoneDeltaTraiList[nextCity-1][city-1]+=self.Q/ant.CurrLen lastCity=ant.TabuCityList[-1] firstCity=ant.TabuCityList[0] PheromoneDeltaTraiList[lastCity-1][firstCity-1]+=self.Q/ant.CurrLen PheromoneDeltaTraiList[firstCity-1][lastCity-1]+=self.Q/ant.CurrLen for(city1,city1x,city1y) in CityList: for(city2,city2x,city2y) in CityList: PheromoneTraiList[city1-1][city2-1]=(1-self.Rou)*PheromoneTraiList[city1-1][city2-1]+PheromoneDeltaTraiList[city1-1][city2-1] PheromoneDeltaTraiList[city1 - 1][city2 - 1]=0 class ANT: #定义蚂蚁类 def __init__(self,currCity=0): self.TabuCitySet=set() #定义禁忌城市集合,定义集合的目的是集合本身要素不重复并且之间可以做差集运算,例如AddCity()方法中 #self.AllowedCitySet=CitySet-self.TabuCitySet 可以方便地从城市集合中去除禁忌城市列表的城市,获取允许的城市列表 self.TabuCityList=[] #定义禁忌城市空列表 self.AllowedCitySet=set() #定义允许城市集合 self.TransferProbabilityList=[] #定义城市选择可能性列表 self.CurrCity=0 #定义当前城市初始值为0 self.CurrLen=0.0 #定义当前旅行路径长度 self.AddCity(currCity) #执行AddCity()方法,获取每次迭代的当前城市CurrCity,禁忌城市列表TabuCityList和允许城市列表AllowedCitySet的值 def SelectNextCity(self,alpha,beta): #定义蚂蚁选择下一个城市的方法,需要参考前文描述的蚁群算法 if len(self.AllowedCitySet)==0: #如果允许城市集合为0,则返回0 return (0) sumProbability=0.0 #定义概率,可能性初始值为0 self.TransferProbabilityList=[] #建立选择下一个城市可能性空列表 for city in self.AllowedCitySet: #循环遍历允许城市集合 sumProbability=sumProbability+(pow(PheromoneTraiList[self.CurrCity-1][city-1],alpha)*pow(1.0/CityDistanceList[self.CurrCity-1][city-1],beta)) #蚂蚁选择下一个城市的可能性由信息素与城市间距离之间关系等综合因素确定,其中alpha为表征信息素重要程度的参数,beta为表征启发式因子重要程度的参数 transferProbability=sumProbability #根据信息素选择公式和轮盘选择得出概率列表,非0-1 self.TransferProbabilityList.append((city,transferProbability)) #将城市序号和对应的转移城市概率追加到转移概率列表中 threshold=sumProbability*random.random() #将概率乘以一个0-1的随机数,获取轮盘制指针值 for(cityNum,cityProb) in self.TransferProbabilityList: if threshold<=cityProb: return (cityNum) return (0) def AddCity(self,city): #定义增加城市到禁忌城市列表中的方法 if city<=0: return self.CurrCity=city #更新当前城市序号 self.TabuCityList.append(city) #将当前城市追加到禁忌城市列表中,因为已经旅行过的城市不应该再进入 self.TabuCitySet.add(city) #将当前城市追加到禁忌城市集合中,用于差集运算 self.AllowedCitySet=CitySet-self.TabuCitySet #使用集合差集的方法获取允许的城市列表 def MoveToNextCity(self,alpha,beta): #定义转移城市方法 nextCity=self.SelectNextCity(alpha,beta) if nextCity > 0: self.AddCity(nextCity) #执行self.AddCity()方法 def ClearTabu(self): self.TabuCityList=[] self.TabuCitySet.clear() self.AllowedCitySet=CitySet-self.TabuCitySet def UpdatePathLen(self): for city in self.TabuCityList[0:-1]:#循环遍历禁忌城市列表 nextCity=self.TabuCityList[self.TabuCityList.index(city)+1] #获取禁忌城市列表中的下一个城市序号 self.CurrLen=self.CurrLen+CityDistanceList[city-1][nextCity-1] #从城市间距离之中提取当前循环城市与下一个城市之间的距离,并逐次求和 lastCity=self.TabuCityList[-1] #提取禁列表中的最后一个城市 firstCity=self.TabuCityList[0] #提取禁忌列表中的第一个城市 self.CurrLen=self.CurrLen+CityDistanceList[lastCity-1][firstCity-1] def two_opt_search(self): #领域搜索 cityNum=len(CityList) for i in range(cityNum): for j in range(cityNum-1,i,-1): curCity1=self.TabuCityList[i]-1 preCity1=self.TabuCityList[(i-1)%cityNum]-1 nextCity1=self.TabuCityList[(i+1)%cityNum]-1 curCity2=self.TabuCityList[j]-1 preCity2=self.TabuCityList[(j-1)%cityNum]-1 nextCity2=self.TabuCityList[(j+1)%cityNum]-1 CurrLen=CityDistanceList[preCity1][curCity1]+CityDistanceList[curCity2][nextCity2] NextLen=CityDistanceList[preCity1][curCity2]+CityDistanceList[curCity1][nextCity2] if NextLen < CurrLen: tempList=self.TabuCityList[i:j+1] self.TabuCityList[i:j+1]=tempList[::-1] if __name__=='__main__': theBaca=BACA() theBaca.ReadCityInfo('eil511.tsp') theBaca.Search()