傅里叶变换的意义
为什么我们要用正弦曲线来代替原来的曲线呢?如果我们也还可以用方波或三角波来代替,分解信号的方法是无穷的,但分解信号的目的是为了更加简单地处理原来的信号。用正余弦来表示原信号会更加简单,因为正余弦拥有其他信号所不具备的性质:正弦曲线保真度。一个正弦曲线信号输入后,输出的仍是正弦曲线,只有幅度和相位可能发生变化,但是频率和波的形状仍是一样的,且只有正弦曲线才拥有这样的性质,正因如此我们才不用方波或三角波来表示。
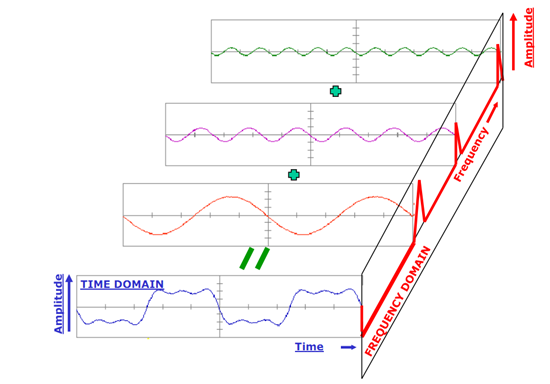
FFT理解
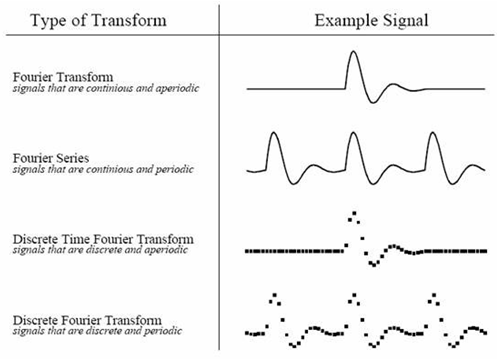
FFT是离散傅立叶变换(DFT)的快速算法,这里我们要讨论是离散信号,对于连续信号我们不作讨论,因为计算机只能处理离散的数值信号,我们的最终目的是运用计算机来处理信号的。所以对于离散信号的变换只有离散傅立叶变换(DFT)才能被适用,对于计算机来说只有离散的和有限长度的数据才能被处理。
示波器采样得到的数字信号,就可以做FFT变换了。N个采样点,经过FFT之后,就可以得到N个点的FFT结果。为了方便进行FFT运算,通常N取2的整数次方。假设采样频率为Fs,信号频率F,采样点数为N。那么FFT之后结果就是N个复数的点。每一个点就对应着一个频率点。这个点的模值,就是该频率值下的幅度特性。
FFT变换前后的频率分辨率
1024Hz的采样率采样1024点,刚好是1秒,也就是说,采样1秒时间的信号并做FFT,则结果可以分析精确到1Hz,如果采样2秒时间的信号并做FFT,则结果可以分析精确到0.5Hz。如果要提高频率分辨率,则必须增加采样点数,也即采样时间。频率分辨率和采样时间是倒数关系。

FFT变换前后的频谱宽度
根据Nyquist采样定理,FFT之后的频谱宽度(Frequency Span)最大只能是原始信号采样率的1/2,如果原始信号采样率是4GS/s,那么FFT之后的频宽最多只能是2GHz。时域信号采样周期(Sample Period)的倒数,即采样率(Sample Rate)乘上一个固定的系数即是变换之后频谱的宽度,即 Frequency Span = K*(1/ΔT),其中ΔT为采样周期,K值取决于我们在进行FFT之前是否对原始信号进行降采样(抽点),因为这样可以降低FFT的运算量。

总结
更高的频谱分辨率要求有更长的采样时间,更宽的频谱分布需要提高对于原始信号的采样率,当然我们希望频谱更宽,分辨率更精确,那么示波器的长存储就是必要的!它能提供您在高采样率下采集更长时间信号的能力!