损失函数、代价函数、目标函数的区别

来自：https://www.cnblogs.com/Belter/p/6653773.html

损失函数，代价函数，目标函数区别

损失函数：定义在单个样本上，一个样本的误差。

代价函数：定义在整个训练集上，所有样本的误差，也就是损失函数的平均。

目标函数：最终优化的函数。等于经验风险+结构风险（Cost Function+正则化项）。

目标函数和代价函数的区别还有一种通俗的区别：

目标函数最大化或者最小化，而代价函数是最小化。

代价函数

训练模型的过程就是优化代价函数的过程，

代价函数对每个参数的偏导数就是梯度下降中提到的梯度，

防止过拟合时添加的正则化项也是加在代价函数后面的。

1.什么是代价函数？

假设有训练样本(x, y)，模型为h，参数为θ。h(θ) = θ^Tx（θ^T表示θ的转置）。

（1）预测出来的值h(θ)与真实值y之间的差异的函数叫做代价函数C(θ)，如果有多个样本，则可以将所有损失函数的取值求均值，记做J(θ)。得出以下代价函数的性质：

1. 每种算法代价函数不唯一；
2. 代价函数是参数θ的函数；
3. 总的代价函数J(θ)可以用来评价模型的好坏，代价函数越小说明模型和参数越符合训练样本(x, y)；
4. J(θ)是一个标量；

（2）确定了模型h，后面做的所有事情就是训练模型的参数θ。取到代价函数J最小值时，就得到了最优的参数θ，记为：

minJ(θ)

例如，J(θ) = 0，表示模型完美的拟合了数据，没任何误差。

（3）在优化参数θ的过程中，最常用的方法是梯度下降，这里的梯度就是代价函数J(θ)对θ₁, θ₂, ..., θ_n的偏导数。

注意：由于求偏导，得到另一个关于代价函数的性质：选择代价函数时，挑选对参数θ可微的函数（全微分存在，偏导数一定存在）

 

2.代价函数的常见形式

 

2.1均方误差

线性回归中，最常用的是均方误差，具体形式为：

 m：训练样本个数；

h_θ(x)：用参数Θ和x预测出来的y值；

y：原训练样本中的y值，也就是标准答案

上坐标(i)：第i个样本

2.2交叉熵

在逻辑回归中，最常用的代价函数是交叉熵（Cross Entropy），交叉熵是一个常见的代价函数，在神经网络中也会用到。

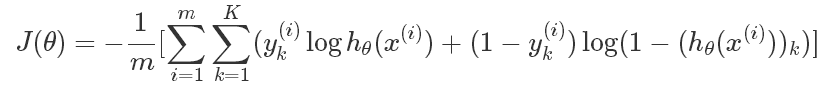
这里多了一层求和项，是因为神经网络的输出一般都不是单一的值，K表示多分类中的类型数。

例如在数字识别中，K=10，表示分了10类。此时对于某一样本来说，输出结果如下：

  1.1266e-004
  1.7413e-003
  2.5270e-003
  1.8403e-005
  9.3626e-003
  3.9927e-003
  5.5152e-003
  4.0147e-004
  6.4807e-003
  9.9573e-001

一个10维的列向量，预测的结果表示输入的数字是0~9中的某一个的概率，概率最大的就被当做是预测结果。例如上面预测结果是9。理想情况下的预测结果应该如下（9的概率是1，其他都是0）：

   0
   0
   0
   0
   0
   0
   0
   0
   0
   1

比较预测结果和理想情况下的结果，可以看到这两个向量的对应元素之间都存在差异，共10组，这里的10表示代价函数里的K，相当于把每一种类型的差异都累加起来了。

3.代价函数与梯度

梯度下降中的梯度指的是代价函数对各个参数的偏导数，偏导数的方向决定了在学习过程中参数下降的方向，学习率（通常用α表示）决定了每步变化的步长，有了导数和学习率就可以使用梯度下降算法（Gradient Descent Algorithm）更新参数。下图展示了只有两个参数的模型运用梯度下降算法的过程。