计量值控制图

（一）SPC与常规控制图

（二）计量值控制图

（三）计件值控制图

（四）计点值控制图

　　表4-1所示的4种计量控制图中，目前均值-标准差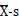（）控制图、均值-极差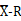（）控制图应用广泛。

1. “ 均值-标准差“控制图

1. “均值-标准差”控制图的控制限

　　参数x的总体服从均值为μ、标准差为σ的正态分布，即x~N（μ，σ²），若定期抽取容量为n的子样（x₁,x₂,......x_n），可得每组样本的均值和标准差为：

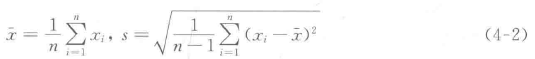
（1）均值控制图的控制限

　　均值 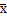服从的分布 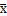~N(μ，σ²/n)，其期望值等于母体分布的均值 μ，标准差为母体标准差的1/ 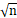倍。均值控制图的中心线CL、上控制限UCL、下控制限LCL为公式（4-3）：

UCL = μ + 3（σ/）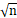

CL = μ　

LCL = μ - 3（σ/）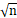

由 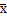控制图可以检测参数中心值的起伏变化。

（2）标准差控制图的控制限

　　记每组子样标准差 s 的期望值和标准差分别为 μ_s、σ_s，标准差控制图的CL、UCL、LCL的计算公式（4-4）：

UCL = μ_s + 3σ_s

CL = μ_s

LCL = μ_s - 3σ_s

由 s 控制图可以监测参数分散性的起伏变化。

2. 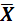- s 图控制限的计算公式

公式（4-3）、（4-4）关键是计算μ、σ、μ_s、σ_s四个未知参数。

若连续采集 k 批数据，计算得到 k 批子样的均值和标准差为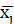（，s_j）。

（1）μ 和 μ_s

数据批次一般不小于25，至少不得小于20。可用多批子样的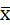均值的平均值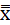（）作为 μ 的估计值：

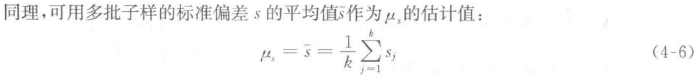
根据上述表达式，只要分别对每批测量数据的均值 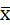  以及标准差 s 求均值，可得到母体分布的 μ 以及s 分布的  μ_s。

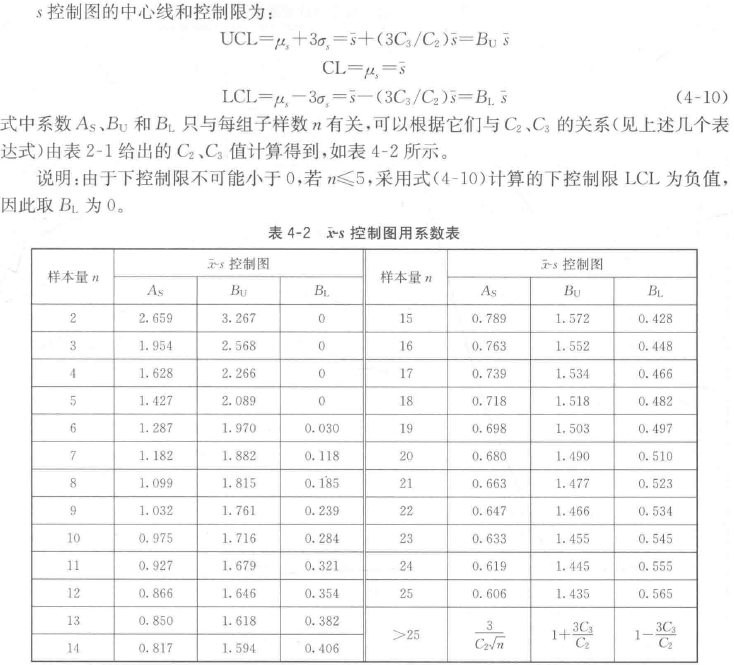
3. “均值-标准差”控制图的应用实例

举例：25批（每批8个）数据，采用“均值-标准差”评价是否处于统计受控状态。

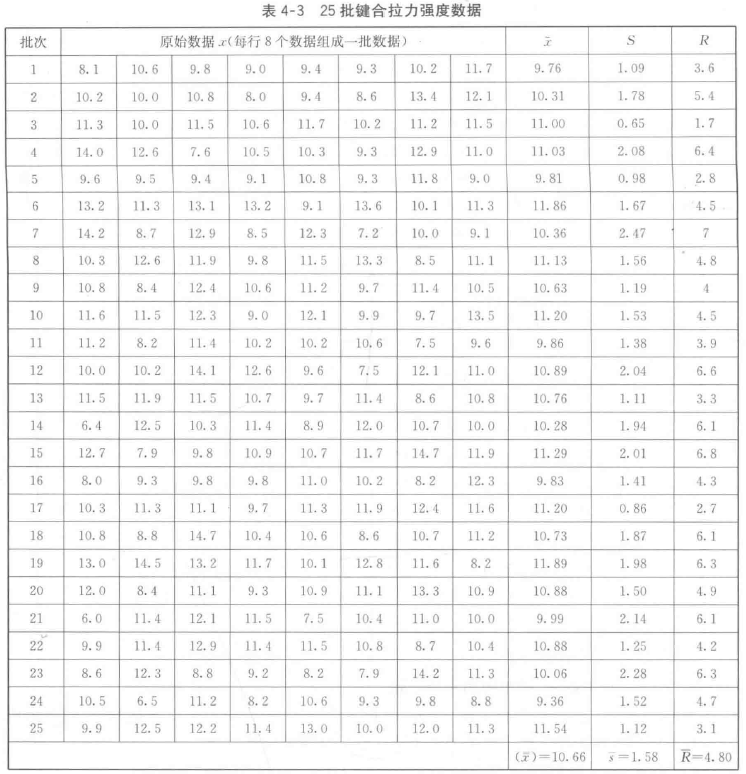
1. 计算每批数据的均值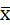和标准差S。结果如表4-3。（均值-极差控制图同理，表中最后一列给出了极差结果）

2. 计算25批数据均值的平均值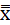（）和标准偏差S的平均值 。

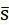3. 采用式（4-9）和式（4-10）计算均值控制图和标准差控制图的中心线和控制限。

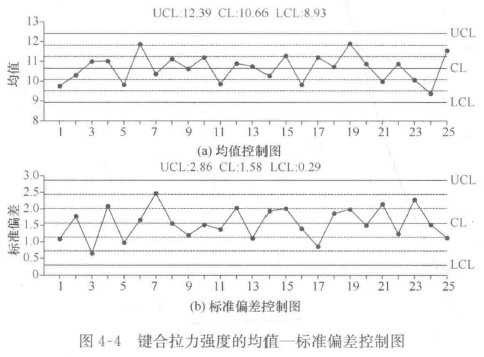
4. 绘制控制图：在控制图上画出控制限，同时将每批数据的均值和标准差分别表示在均值控制图和标准差控制图上，即完成开工制图的绘制。如图4-4.

5. 统计受控状态的判断。

2. “ 均值-极差“控制图

1. “均值-极差”控制图的控制限

 

 

 

3. “均值-极差”控制图的应用实例 

3. “ 单值-移动极差“控制图

1. “单值-移动极差”控制图

实际生产中，有时每批样本只包含一个数据，即 n = 1。这种情况可以采用“单值-移动极差”控制图（又记为 x-R_s 控制图）分析统计受控状态。

将每批的一个数据值直接标示在控制图上就是单值控制图。移动极差指相邻两批数据之差的绝对值。将移动极差值标示在控制图上就是 Rs 控制图。

2. “单值-移动极差”控制图的构成特点

由于每批数据只有一个数据，与 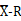控制图相比，有以下几个特点：

（1）每批中的一个数据对应于均值控制图中每批数据的均值。

（2）用相邻两批数据之差的绝对值对应极差控制图中每批数据的极差。如果一共有k批数据，则只有（k-1）个移动极差值，即第一批不存在对应的移动极差数据。

（3）计算移动极差只涉及相邻两个数据。因此采用式（4-16）从移动极差数据平均值计算母体分布的标准偏差时，公式中的d₂值应该取为与两个数据（n=2）对应的值。

3.  x-R_s 控制图的控制限计算公式

4. “单值-移动极差”控制图的应用实例

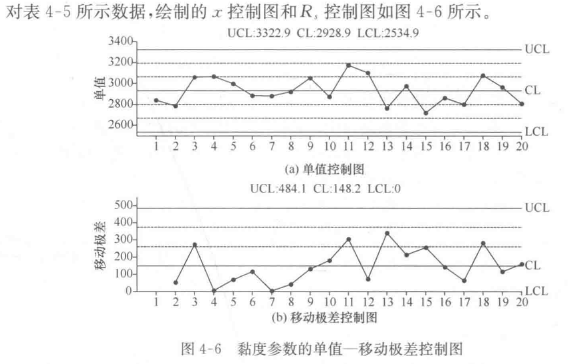
以下面的数据为例，采用单值-移动极差控制图评价该工序生产过程中是否处于统计受控状态。

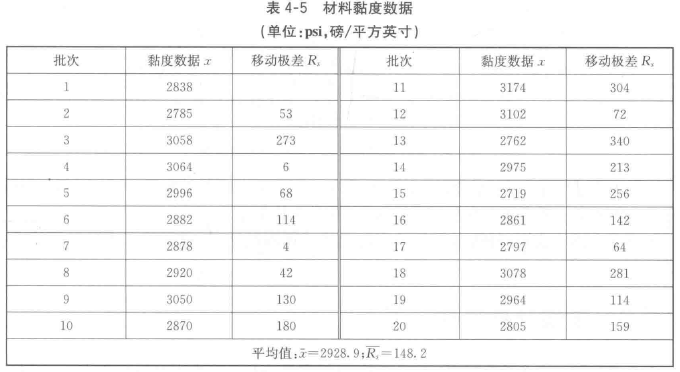
（1）计算相邻两批数据之差的绝对值作为移动极差 (R_s)_j = |x_j+i - x_j|。结果如表4-5，对20批数据，只有19个移动极差值。

（2）计算20批数据的平均值，计算19个移动极差数据的平均值。如表4-5最后一行所示。

（3）采用式（4-20）、式（4-21）计算单值控制图和移动极差控制图的中心线和上下控制限。

（4）绘制控制图：在控制图上画出控制限，同时将每批数据和移动极差值分别标示在单值控制图和移动极差控制图。

根据判断规则判断是否有失控情况。