【C/C++】二维数组的传参的方法/二维字符数组的声明，使用，输入，传参

【问题】
定义了一个子函数，传参的内容是一个二维数组

编译提示错误
因为多维数组作为形参传入时，必须声明除第一位维外的确定值，否则系统无法编译（算不出偏移地址）

【二维数组的传参】
方法一：形参为二维数组，并给出第二维长度
举例：

#include <stdio.h>
 
void subfun(int n, char subargs[][5])
{
    int i;
    for (i = 0; i < n; i++) {
    	printf("subargs[%d] = %s
", i, subargs[i]);
    }
}
 
void main()
{
    char args[][5] = {"abc", "def", "ghi"};
    subfun(3, args);
}

方法二：形参作为指向数组的指针并给出数组长度

#include <stdio.h>
 
void subfun(int n, char (*subargs)[5])
{
    int i;
    for (i = 0; i < n; i++) {
    	printf("subargs[%d] = %s
", i, subargs[i]);
    }
}
 
void main()
{
    char args[][5] = {"abc", "cde", "ghi"};
    subfun(3, args);
}

我用了这个方法：

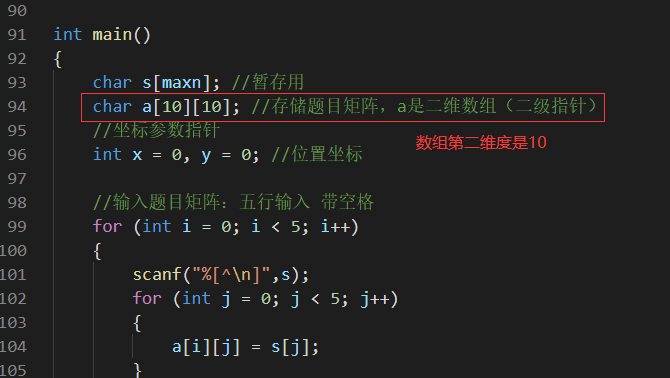
方法三：形参为指针的指针
实参必须有指针，不能为数组名

#include <stdio.h>
 
void subfun(int n, char **subargs)
{
    int i; 
    for (i = 0; i < n; i++) {
    	printf("subargs[%d] = %s
", i, subargs[i]);
    }
}
 
void main()
{
    //char* a[3]是一个指针，a[0]存储的是args[0][0]的地址，a[1]存储的是args[1][0]的地址，a[2]存储的是args[2][0]的地址。
    char *a[3];
    char args[][5] = {"abc", "def", "ghi"};
    a[0] = args[0];  //equals with a[0] = &args[0][0];
    a[1] = args[1];
    a[2] = args[2];
    subfun(3, a);  //若此处为subfun(3, args);则会编译出错
//a的值是a[0]的地址，所以a = &args[0];
}

上述代码等价于下面代码。

#include <stdio.h>
 
void subfun(int n, char **subargs)
{
    int i; 
    for (i = 0; i < n; i++) {
    	printf("subargs[%d] = %s
", i, subargs[i]);
    }
}
 
void main()
{
    char *args[] = {"abc", "def", "ghi"};//equals with char *args[3] = {"abc", "def", "ghi"};
    subfun(3, args);
}

【总结】二维字符数组的创建和引用的最佳方法
传参，输出：

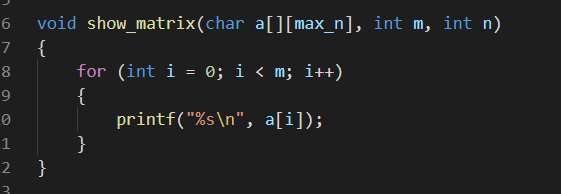
声明还是这样比较易懂：

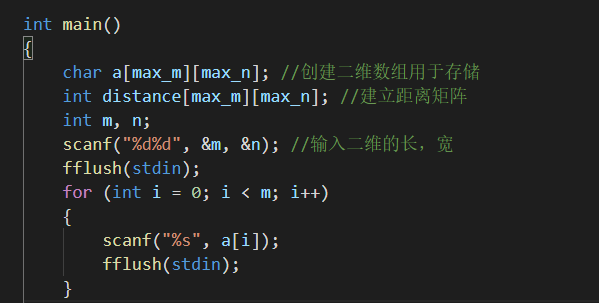
上述的第三种方法我还是不太会

【参考资料】
C/C++二维数组传参方法总结 https://blog.csdn.net/gqb_driver/article/details/8886687