题目链接:http://acm.split.hdu.edu.cn/showproblem.php?pid=5855
题意:有n个工厂m个商店,建造工厂需要花费pay和时间t,商店需要指定的几个工厂供货,如果同时供货的话可以获利pro。要求时间最小的情况下获利最多,求最小时间和最小时间下最大获利。
岐爷博客学习了:http://www.cnblogs.com/wuyiqi/archive/2012/03/12/2391960.html
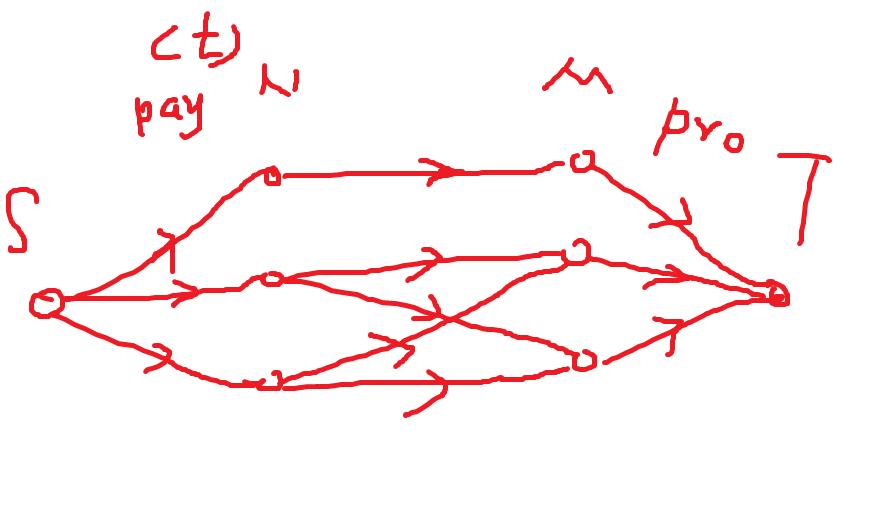
这个图是这么建的。先读入数据后在区间(0~tmax)二分枚举时间time,代表当前建造时间不超过time的工厂可以同时建造。
之后就是求最大权闭合图,最大权闭合图的的权 = 原图中权值为正的点的和(所有用户的收益之和) - 最小割(最大流)
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 typedef struct Edge { 5 int u, v, w, next; 6 }Edge; 7 8 const int inf = 0x7f7f7f7f; 9 const int maxn = 2020; 10 11 int cnt, dhead[maxn]; 12 int cur[maxn], dd[maxn]; 13 Edge dedge[20202020]; 14 int S, T, N; 15 16 void init() { 17 memset(dhead, -1, sizeof(dhead)); 18 for(int i = 0; i < maxn; i++) dedge[i].next = -1; 19 S = 0; cnt = 0; 20 } 21 22 void adde(int u, int v, int w, int c1=0) { 23 dedge[cnt].u = u; dedge[cnt].v = v; dedge[cnt].w = w; 24 dedge[cnt].next = dhead[u]; dhead[u] = cnt++; 25 dedge[cnt].u = v; dedge[cnt].v = u; dedge[cnt].w = c1; 26 dedge[cnt].next = dhead[v]; dhead[v] = cnt++; 27 } 28 29 bool bfs(int s, int t, int n) { 30 queue<int> q; 31 for(int i = 0; i < n; i++) dd[i] = inf; 32 dd[s] = 0; 33 q.push(s); 34 while(!q.empty()) { 35 int u = q.front(); q.pop(); 36 for(int i = dhead[u]; ~i; i = dedge[i].next) { 37 if(dd[dedge[i].v] > dd[u] + 1 && dedge[i].w > 0) { 38 dd[dedge[i].v] = dd[u] + 1; 39 if(dedge[i].v == t) return 1; 40 q.push(dedge[i].v); 41 } 42 } 43 } 44 return 0; 45 } 46 47 int dinic(int s, int t, int n) { 48 int st[maxn], top; 49 int u; 50 int flow = 0; 51 while(bfs(s, t, n)) { 52 for(int i = 0; i < n; i++) cur[i] = dhead[i]; 53 u = s; top = 0; 54 while(cur[s] != -1) { 55 if(u == t) { 56 int tp = inf; 57 for(int i = top - 1; i >= 0; i--) { 58 tp = min(tp, dedge[st[i]].w); 59 } 60 flow += tp; 61 for(int i = top - 1; i >= 0; i--) { 62 dedge[st[i]].w -= tp; 63 dedge[st[i] ^ 1].w += tp; 64 if(dedge[st[i]].w == 0) top = i; 65 } 66 u = dedge[st[top]].u; 67 } 68 else if(cur[u] != -1 && dedge[cur[u]].w > 0 && dd[u] + 1 == dd[dedge[cur[u]].v]) { 69 st[top++] = cur[u]; 70 u = dedge[cur[u]].v; 71 } 72 else { 73 while(u != s && cur[u] == -1) { 74 u = dedge[st[--top]].u; 75 } 76 cur[u] = dedge[cur[u]].next; 77 } 78 } 79 } 80 return flow; 81 } 82 83 inline bool scan_d(int &num) { 84 char in;bool IsN=false; 85 in=getchar(); 86 if(in==EOF) return false; 87 while(in!='-'&&(in<'0'||in>'9')) in=getchar(); 88 if(in=='-'){ IsN=true;num=0;} 89 else num=in-'0'; 90 while(in=getchar(),in>='0'&&in<='9'){ 91 num*=10,num+=in-'0'; 92 } 93 if(IsN) num=-num; 94 return true; 95 } 96 97 int n, m, L; 98 int pay[maxn], t[maxn], pro[maxn]; 99 int k[maxn]; 100 int G[maxn][maxn]; 101 int maxx; 102 103 int main() { 104 // freopen("in", "r", stdin); 105 int tt, _ = 1; 106 scan_d(tt); 107 while(tt--) { 108 maxx = -1; 109 memset(G, 0, sizeof(G)); 110 scan_d(n); scan_d(m); scan_d(L); 111 for(int i = 1; i <= n; i++) { 112 scan_d(pay[i]); scan_d(t[i]); 113 maxx = max(maxx, t[i]); 114 } 115 for(int i = 1; i <= m; i++) { 116 scan_d(pro[i]); scan_d(k[i]); 117 for(int j = 0; j < k[i]; j++) { 118 scan_d(G[i][j]); 119 } 120 } 121 int lo = 0, hi = maxx + 1; 122 int ret1 = -1, ret2 = 0; 123 while(lo <= hi) { 124 init(); 125 S = 0, T = n + m + 1, N = T + 1; 126 int mid = (lo + hi) >> 1; 127 for(int i = 1; i <= n; i++) { 128 if(mid >= t[i]) adde(S, i, pay[i]); 129 else adde(S, i, inf); 130 } 131 int pos = 0; 132 for(int i = 1; i <= m; i++) { 133 for(int j = 0; j < k[i]; j++) { 134 adde(G[i][j], i+n, inf); 135 } 136 adde(i+n, T, pro[i]); 137 pos += pro[i]; 138 } 139 int flow = dinic(S, T, N); 140 if(pos - flow >= L) { 141 hi = mid - 1; 142 ret1 = mid, ret2 = pos - flow; 143 } 144 else lo = mid + 1; 145 } 146 if(ret1 == -1) printf("Case #%d: impossible ", _++); 147 else printf("Case #%d: %d %d ", _++, ret1, ret2); 148 } 149 return 0; 150 }