如何判断两天线是否接近平行。

我有两条线，我想知道他们是否平行。每条线用两点表示 (x1,y1,z1),(x2,y2,z2)。

重要的条件是允许存在轻微的角度阈值误差。

例如：如果两线之间的角度<5度，则就认为他们仍然是平行的。

我的想法是

一：

两条线通过计算(x2,y2、z2)−(x1,y1,z1)，创建矢量指向沿着每个线方向。

让他们成为单位向量除以他们按长度。这两个单位向量为u和v。

使用inner product内积<u,v>=cos(θ),θ 就是两个向量的角度。

可以创建两个很小的阈值作为范围[-1,1]。当点积接近1的时候说明两个向量在相同方向很接近。

如果接近-1则在不同方向很接近。

二：

两条线找到两个向量 a,b。然后检查一下公式。

.是点积，x是向量积。ϵ 就是允许的角度误差。

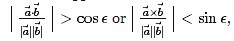
小弟不才，如有欠缺，还请多多指教。

 解决方法：

    vector<cv::Point2f> vec; 
    vec.push_back(cv::Point2f(0,0)); 
    vec.push_back(cv::Point2f(10,0)); 
    vec.push_back(cv::Point2f(10,10)); 
    vec.push_back(cv::Point2f(0,10)); 
    vec.push_back(cv::Point2f(5,5)); 

    cv::Point2f A=vec[4],B=vec[3],C=vec[3],D=vec[2];

    cv::Point2f AB=B.x>A.x?(B-A):(A-B);//x方向从小到大
    cv::Point2f CD=D.x>C.x?(D-C):(C-D);//x方向从小到大

    double abm=sqrt(pow(AB.x,2)+pow(AB.y,2));//|AB|求向量模
    double cdm=sqrt(pow(CD.x,2)+pow(CD.y,2));//|CD|求向量模
    double ret=(AB.x*CD.x+AB.y*CD.y)/(abm*cdm);
    double angle=acos(ret)/CV_PI*180;//反余弦，弧度转换角度