动态规划矩阵连乘问题

矩阵连乘问题是动态规划的重要例子，弄了一个晚上加一个小时终于AC了。。。。感觉自己很拙。。。。。

矩阵链乘问题

输入：

共两行

第一行 N （ 1<=N<=100 ），代表矩阵个数。

第二行有 N+1 个数，分别为 A1 、 A2 …… An+1 （ 1<=Ak<=10 ）， Ak 和 Ak+1 代表第 k 个矩阵是个 Ak X Ak+1 形的。

输出：

共两行

第一行 M ，为最优代价。注：测试用例中 M 值保证小于 2^31

第二行为最优顺序。如 (A1((A2A3)A4)) ，最外层也加括号。

注意:测试用例已经保证了输出结果唯一,所以没有AAA的情况.

解：

算法其实不难，就是填表，注意填表时的顺序，应该是斜线填充，一次填一根斜线。

动态规划递归方程的建立：

    子问题状态的建模（很关键）：令m[i][j]表示第i个矩阵至第j个矩阵这段的最优解。
      显然如果i=j，则m[i][j]这段中就一个矩阵，需要计算的次数为0；
        如果i>j，则m[i][j]=min{m[i][k]+m[k+1][j]+p[i-1]Xp[k]Xp[j]},其中k,在i与j之间游荡，所以i<=k<j ;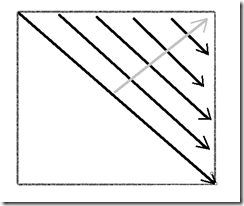

这一段算法不难，问题是输出。弄了好久想了好几种方法都没成功。

书上的算法貌似不对，递归倒是用的递归，但是书上的递归输出有问题。。。。好罗嗦

正确的输出代码应该是这样的：

void print(int i, int n, int point[][101])
{
	if(i == n) {printf("A%d", i);}
	else if(i+1 == n) printf("(A%dA%d)", i, n);
	else {
		printf("(");
		print(i, point[i][n], point);
		print(point[i][n]+1, n,point);
		printf(")");
	}
}

整体代码如下，仅供参考：

#include"stdafx.h"
#include"stdio.h"
#include<stdlib.h>

#define MAX 101

void print(int i, int n, int point[][101])
{
	if(i == n) {printf("A%d", i);}
	else if(i+1 == n) printf("(A%dA%d)", i, n);
	else {
		printf("(");
		print(i, point[i][n], point);
		print(point[i][n]+1, n,point);
		printf(")");
	}
}

int main()
{
	int n, i, j, k, t, temp_value, a[MAX], point[MAX][MAX], times[MAX][MAX];
	//long int ans;
	scanf("%d", &n);
	for(i = 0; i <= n; i++) 
		scanf("%d", &a[i]);
	for(i = 1; i <= n; i++) {times[i][i] = 0;}
	for(k = 2; k <= n; k++) {	//斜线方向
		for(i = 1; i <= n - k + 1; i++) {	//斜下
			j = k +i - 1;//
			times[i][j] = times[i+1][j] + a[i-1] * a[i] * a[j];//从j-1得到
			point[i][j] = i;
			for(t = i+1; t < j; t++) {
				temp_value = times[i][t] + times[t+1][j] + a[i-1]*a[t]*a[j];
				if(times[i][j] > temp_value) {
					times[i][j] = temp_value;
					point[i][j] = t;
				}//if
			}//for t
		}//for i
	}//for k

	//输出顺序
	printf("%d\n", times[1][n]);
	if(n == 1) printf("(A1)\n"); 
	else {
	print(1, n, point);
	printf("\n");
	}
	system("pause");
	return 0;
}//main