一、纲要
梯度下降法的可视化理解
梯度下降法的公式
参数的更新方法
梯度下降算法最小化代价函数
二、内容介绍
1、梯度下降法的可视化理解
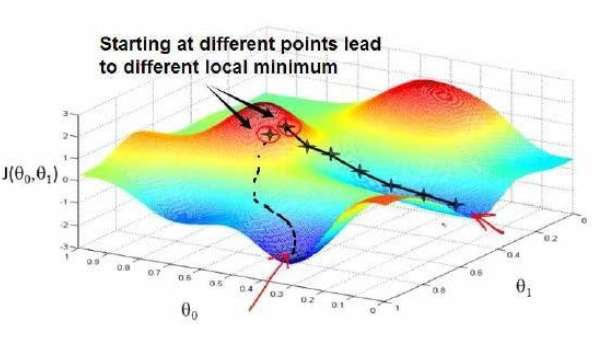
在上篇文章中我说了代价函数的最小化就是要寻找该函数的最小值，或者说是局部最小值。如上图，我们假设红色的为两个山峰，那么蓝色的就是我们要找的最小值。这个过程我们可以想象成某个人下山的过程。当给参数不同的初值。相当于选择了不同的下山起点位置，梯度下降法的过程就相当于一次次的迭代，即对于下山来说，就是每走一步，就停下来观察并选择可以最快下山的路，然后再走一步，然后再次重复这个过程。当然，图上显而易见的是，当我们选择的起点位置不同，就会得到不同的下山路线，最终会到达一个看起来最小的值，所以这也就是我之前为什么说是局部最小值。这样理解梯度下降法看起来更浅显易懂！
2、梯度下降法的公式
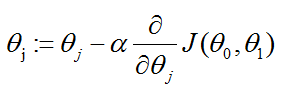，这里的Alpha称为学习速率(learning rate)，就是我们下山时的步伐，是大步流星还是小碎步下山，这当然也决定了下降的速率
我们用一个较为简单的代价函数来解释一下这个公式：J(θ)
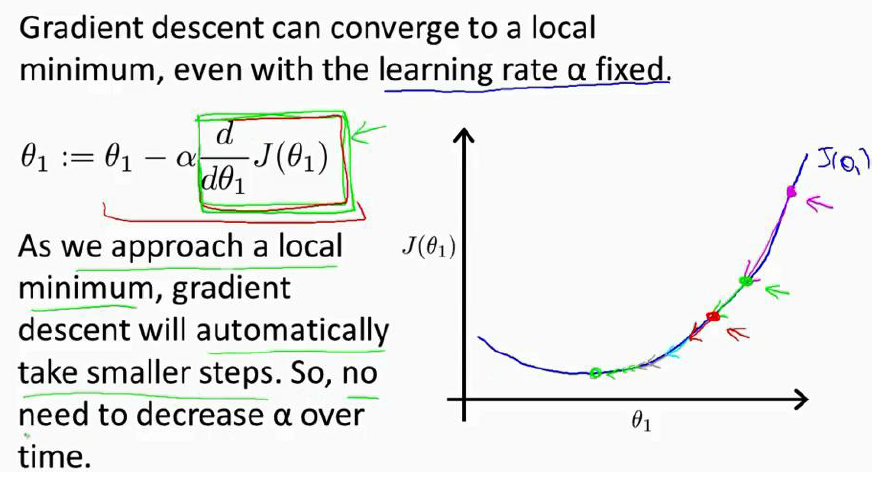
对J的微分就是在该点的斜率，可以很容易的看出不管是该点(起始点)在最低点的左边还是右边，经过数次迭代之后参数θ总是向着J的最低点逼近。
3、参数的更新方法
正确的更新方法： 错误的更新方法：
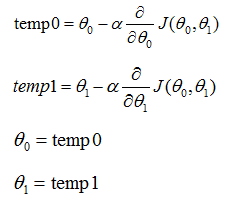
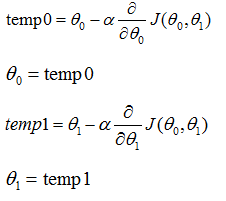
注：这里的theta0和theta1是要同时更新的，如果计算了theta0之后就直接更新theta0的值的话，公式右边的代价函数J就会发生变化，所以需要计算完所有参数的值之后再同时进行更新。
3、用梯度下降法最小化代价函数J
接着上篇的线性回归问题，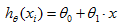
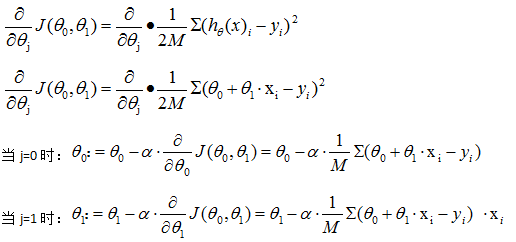
所以，梯度下降方程为：
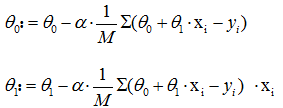
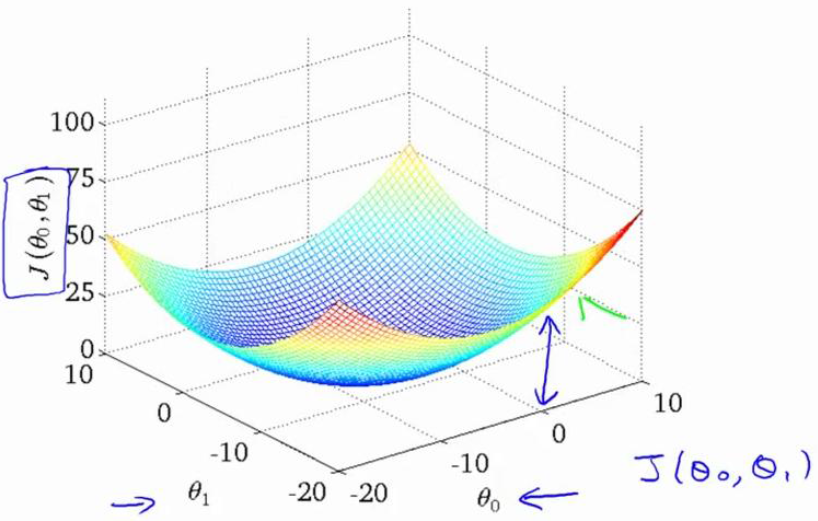
事实证明，如果你的成本函数进行线性回归，他的代价函数将成碗状，即不存在局部最优解，局部最优解自动转化为全局最优。
