一、纲要
逻辑回归
决策边界
拟合逻辑回归的参数θ
多类别分类问题(Multiclass classification)
二、内容详述
1、逻辑回归
逻辑回归,实际上就是一种分类算法,它的性质是输出值应该在[0,1]这个区间,所以对于逻辑回归问题我们的函数h就不再跟前面线性回归的函数一样的形式了,我们这里根据逻辑函数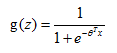 来假设逻辑回归函数
来假设逻辑回归函数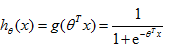 。逻辑函数g(z)和分类函数hθ(x)的曲线如下:
。逻辑函数g(z)和分类函数hθ(x)的曲线如下:
 因此,我们就可以把h控制在[0,1]区间内
因此,我们就可以把h控制在[0,1]区间内
这里需要说明的是,hθ(x)的作用是对于给定输入变量,根据选择的参数计算输出变量等于1的概率,即hθ(x)=P(y=1|θ,x)。一定要注意这里说的是等于1的概率
2、决策边界
决策边界可以帮助我们理解逻辑回归中的假设函数做什么事情。根据上图,我们可以认为,当hθ(x)>=0.5时,y=1,当hθ(x)<0.5时,y=0。当把z换成θTx时
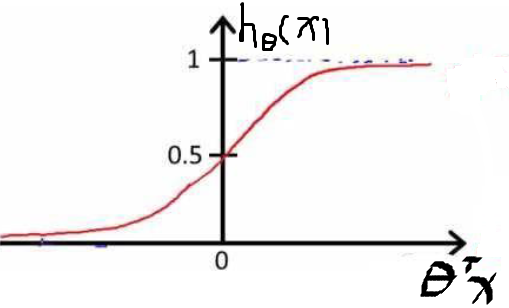
所以,hθ(x)>=0.5我们可以替换成θTx>=0,y=1;θTx<0,y=0。逻辑回归中我们需要做的就是拟合参数θ0,θ1,...θn。我们举一个简单的例子说明什么是决策边界
假设hθ(x)=g(θ0+θ1x1+θ2x2),且θT=[θ0,θ1,θ2]=[-3,1,1],那么带入θTx就变成了当-3+x1+x2>=0时,y=1;当-3+x1+x2<0时,y=0。如图所示
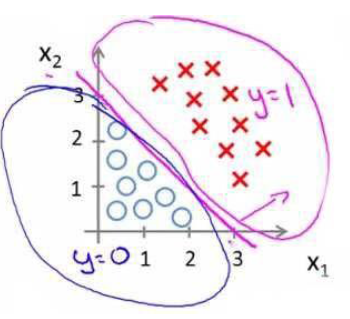
那么这条线 x1+x2=3就是决策边界。当然这是个简单的决策边界,也可以有更复杂的决策边界,这里hθ(x)=g(θ0+θ1x1+θ2x2+θ3x1^2+θ4x2^2)且θ=[-1,0,0,1,1],同样的方法代入后我们会发现决策边界为x1^2+x2^2=1,是个圆。
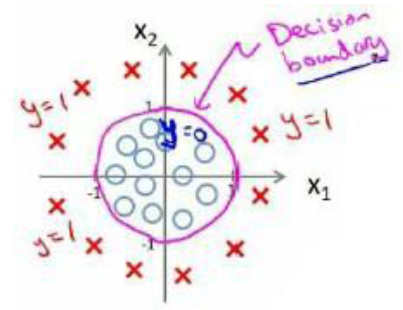
这里需要注意的是,决策边界是参数集θ的属性,就是当参数集[θ0,θ1,...θn]确定了之后,决策边界就确定了,而并非由训练数据集决定(并非由图上的OOXX形成的形状决定)
3、拟合逻辑回归的参数θ
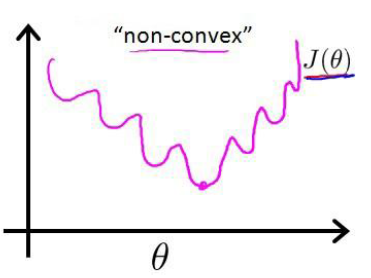
在解决逻辑回归问题时,就不能再用线性回归的代价函数来寻找最优解,因为当我们将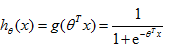 带入代价函数的时候,得到的将是这样的曲线,这就有太多的局部最优解因而不利于我们寻找全局最优解
带入代价函数的时候,得到的将是这样的曲线,这就有太多的局部最优解因而不利于我们寻找全局最优解
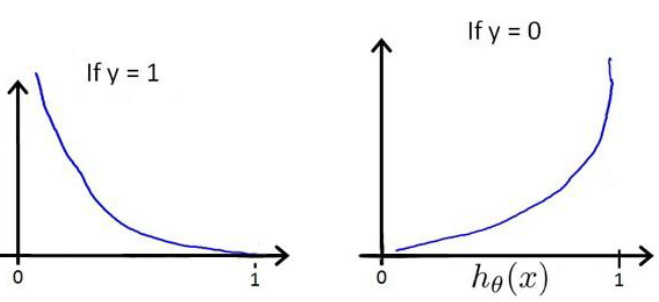
所以重新定义了代价函数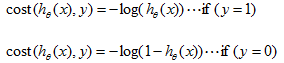 如右上图,y轴为cost(h,y)的值。我们这里可以将两种条件下
如右上图,y轴为cost(h,y)的值。我们这里可以将两种条件下
的cost(h,y)进行合并得到![]() 。代价函数J为
。代价函数J为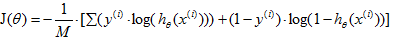 。之后就是同样的J(θ)的最小化问题了。用梯度下降法代入梯度下降公式
。之后就是同样的J(θ)的最小化问题了。用梯度下降法代入梯度下降公式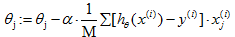 ,我们发现代入梯度下降公式之后得到的与线性回归问题是相同的。
,我们发现代入梯度下降公式之后得到的与线性回归问题是相同的。
4、多类别分类问题
多类别说的是输出值大于2的情况像y=1,y=2,y=3...我们有个新的工具叫做逻辑回归分类器h(i)(x),表示第i个类别的输出,输出的为P(y=i|θ,x)即y=i的概率。假设这样一组数据集,共可以分出3类,y=1,y=2,y=3
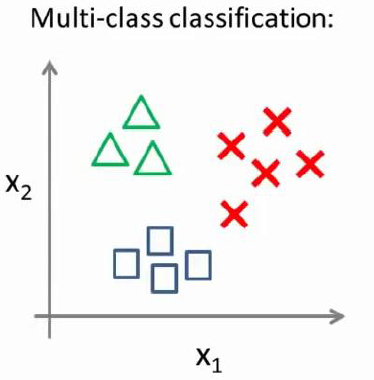
分类器就是先将某两个看成同一类,然后解决这个二元分类问题,然后再换另外两个为一类,再次循环,总共三次,得到
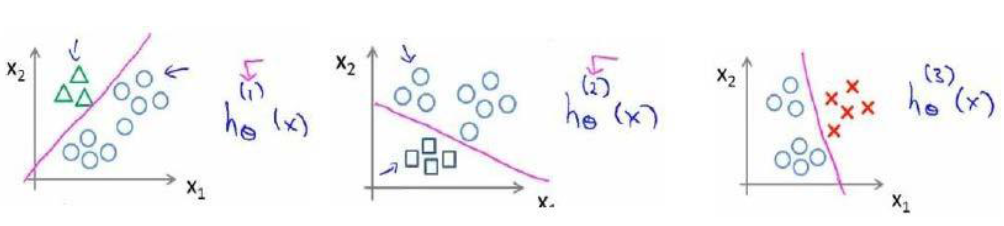
我们在作预测的时候就是将所有的分类机都执行一遍,对每个输入变量,我们选择最高可能性的输出变量最为最终的输出变量,这样就可以解决多类分类问题啦!