已知两条直线(l_1:y=m)和(l_2:y=frac{8}{2m+1}(m>0))
(l_1)与函数(y=|log_2x|)的图像从左到右交点为(A,B),(l_2)与函数(y=|log_2x|)的图像从左到右交点为(C,D)
记线段(AC)在(x)轴上投影长度为(a),线段(BD)在(x)轴上投影长度为(b),求(frac{b}{a})的最小值
解答:
根据题意,图像是一条对数函数的绝对值加两个常函数
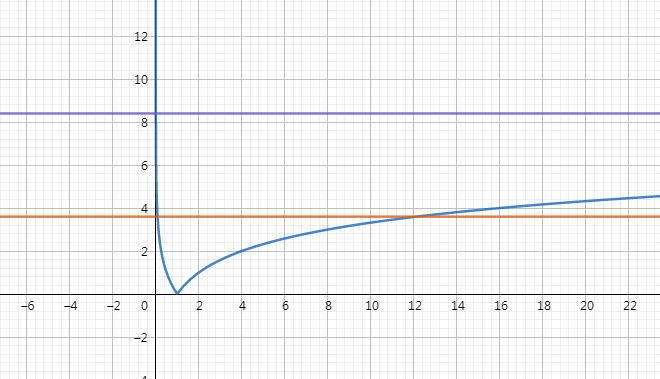
设下面的一条是(l_1),上面那条是(l_2)
联立解析式可以得出
[x_A=2^{-m},x_B=2^m,x_C=2^{-frac{8}{2m+1}},x_D=2^{frac{8}{2m+1}}
]
[frac{b}{a}=frac{|2^{frac{8}{2m+1}}-2^{m}|}{|2^{-m}-2^{-frac{8}{2m+1}}|}
]
[=frac{|2^{frac{8}{2m+1}}-2^{m}|}{|frac{1}{2^{-m}}-frac{1}{2^{frac{8}{2m+1}}}|}
]
[=frac{|2^{frac{8}{2m+1}}-2^{m}|} { |frac{2^m-2^{frac{8}{2m-1}}} {2^m2^{frac{8}{2m-1}}}| }
]
[={2^{m+frac{8}{2m-1}}}
]
显然(2^x)是增函数,考虑让指数最小
[m+frac{8}{2m+1}=frac{1}{2}(2m+1)+frac{8}{2m+1}-frac{1}{2}ge 2sqrt{frac{1}{2}*8}-frac{1}{2}=frac{7}{2}
]
所以(frac{b}{a})最小值为(2^{frac{7}{2}}=8sqrt{2})