计算几何
基础知识
点积
(a·b=a.x*b.x+a.y*b.y)
(a)在(b)上的投影乘以(b)的模长
叉积
(a×b=a.x*b.y-a.y*b.x)
(a,b)围成的平行四边形的有向面积
直线与线段
记录直线上一点和直线方向
线段记录线段端点 或记录线段起点和向量终点
判断线段相交(快速排斥实验与跨立实验)
快速排斥实验:如果以两条线段为对角线的矩形不相交,则两条线段不相交,这是充分不必要条件
跨立实验:由一条线段的端点向另一条线段两端点做叉积,判断符号是否一致,符号不一致则相交,但线段共线时失效
两者结合万无一失
海伦公式
三点共线
((x_1y_2-x_2y_1)+(y_1z_2-y_2z_1)+(z_1x_2-z_2x_1)=0)
围成的三角形面积为(0)
求线段交点
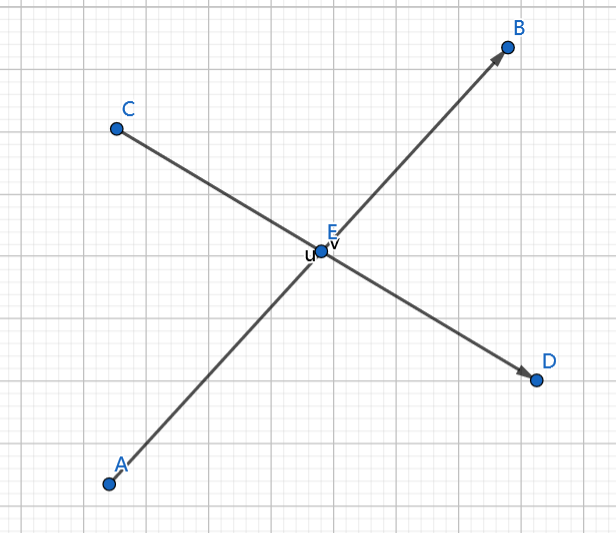
直接解方程太麻烦了
交点(E)在直线(CD)上,根据三点共线的向量公式,(vec{OE}=kvec{OC}+(1-k)vec{OD})
(k:1-k=|CE|:|DE|=S_{▲ABC}:S_{▲ABD})
三角形面积可以用叉积求
交点即为(C)的坐标加上(frac{1}{k})乘以(CD)的斜率
点旋转
旋转( heta)度
向量旋转
逆时针旋转(k)度
inline vector turn (vector a,double k)
{
return vector(a.x*cos(k)-a.y*sin(k),a.x*sin(k)+a.y*cos(k));
}
判断点在多边形内部
光线投射算法:由一点引一条射线,若与多边形有奇数个交点则在多边形内部
回转数算法:
原理:平面内闭合曲线绕过该点总次数为(0)时点在曲线外部
实现:把一点和多边形所有顶点连起来,计算相邻两边有向夹角和,如果夹角和为不为零则在多边形内部
求任意多边形面积
将多边形上的点逆时针排序,选第一个点为辅助点(O),设(v_i=p_i-O),则
极角排序
在平面内取一个定点(O),叫做极点,引一条射线(Ox),叫做极轴,再选定一个长度单位和角度的正方向(通常取逆时针方向)
对于平面内任何一点(M),用(ρ)表示线段(OM)的长度,用( heta)表示(Ox)到(OM)的角度,(ρ)叫做点(M)的极径,( heta)叫做点(M)的极角,有序对((ρ, heta))就叫点(M)的极坐标
极角排序方法1:
用(atan2(y,x))函数按极角从小到大排序
inline bool cmp (node a,node b)
{
double x=atan2(a.y,a.x),y=atan2(b.y,b.x);
return x!=y?x<y:a.x<b.x;
}
曼哈顿距离
(d(A,B)=|x_1-x_2|+|y_1-y_2|)
满足三角不等式(d(i,j)leq d(i,k)+d(k,j))
平面最远曼哈顿距离:求(max{|x_1-x_2|+|y_1-y_2|})
假设(x_1>=x_2)
当(y_1>=y_2)时,(dis=x_1+y_1-(x_2+y_2))
当(y_1<y_2)时,(dis=x_1-y_1-(x_2-y_2))
只要求(max{max(x_i+y_i)-min(x_i+y_i),max(x_i-y_i)-min(x_i-y_i)})
或转切比雪夫距离,预处理横纵坐标最大值
高维最大曼哈顿距离:坑
切比雪夫距离
(d(A,B)=max(|x_1-x_2|,|y_1-y_2|))
曼哈顿与切比雪夫距离互化
(A,B)曼哈顿距离:
这就是((x_1+y_1,x_1-y_1))和((x_2+y_2,x_2-y_2))的切比雪夫距离
曼哈顿距离转切比雪夫距离:((x,y)Rightarrow(x+y,x-y))
新坐标下的切比雪夫距离即为原坐标系下的曼哈顿距离
同理由上式推出,(A,B)的切比雪夫距离:
是((frac{x_1+y_1}{2},frac{x_1-y_1}{2}))和((frac{x_2+y_2}{2},frac{x_2-y_2}{2}))之间的曼哈顿距离
切比雪夫距离转曼哈顿距离:((x,y)Rightarrow(frac{x+y}{2},frac{x-y}{2}))
圆的树形结构
规定内含与圆(A)的圆(B)是(A)的儿子
建树做法:将圆分为上下两个半圆,扫描到上半圆时将该半圆所属圆建立子树并入栈,扫描到下半圆时回溯
二维凸包
求凸包
(Graham)算法:
二维平面上给定(n)个点求凸包
显然左下角的点应该在凸包上
把(y)最小的点同时(x)最小的点(左下角的点)先选出来,将其他点以左下角的点为基准点极角排序
按极角序将点入栈,利用斜率单调性判断是否弹栈
注意极角排序时若极角相同应该让距基准点较近的点放在前面,保证会被弹出
(Andrew)算法:
将所有点按(x)从小到大排序
从第一个点开始,如果下一个点在当前直线的左侧,则入栈
否则将上一个点出栈,再判断
这样一次遍历只会求出一个下凸壳,如果要得到整个凸包要从最后一个点再反向遍历一遍
动态二维凸包
坑
Pick定理
对于顶点均为整点的简单多边形,其面积(S),内部格点数(i),边上格点数(b)满足
(S=i+frac{b}{2}-1)
推广:
在格点面积为(1)的空间中,格点是平行四边形则皮克定理适用
格点是三角形则(S=2*i+b-2)
旋转卡壳
求凸包直径:
首先不能用双指针法扫描点对
考虑以下情况:
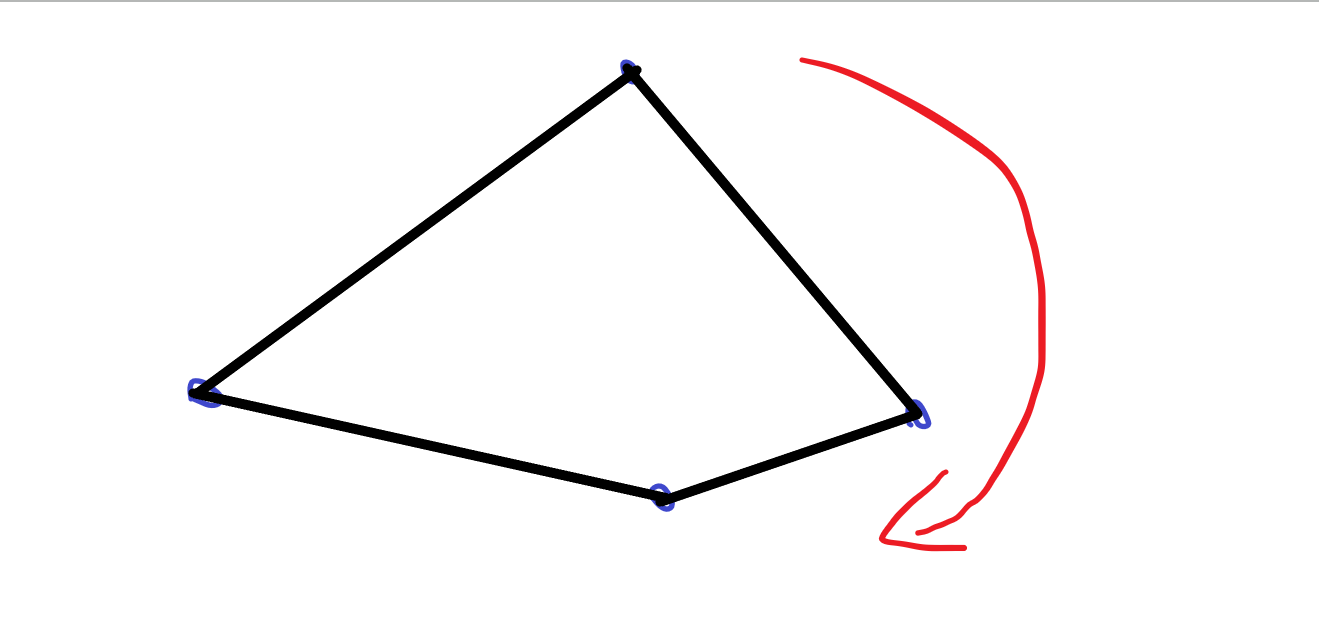
此时并不能保证点对之间距离是单调增的
改变一下思路,如果一个点到一条边的距离最远,那么它到这条边的两个端点中的一个一定是最远的
怎么找距离一条边最远的点(或距离一个点最远的边)呢?
考虑旋转卡壳
如果我们枚举边,那么一条边和另外一点形成的三角形的底固定,则三角形面积越大,点和直线距离越大,所以我们可以用叉积快速算面积,通过双指针找到每条边的面积峰值
这个过程就像有两条斜率相等的直线,一条直线与凸包的一条边重合,另一条直线在凸包的另一个刚好卡住了一个距离该直线最远的顶点
半平面交
给定(n)条直线,每条直线留下左半部分,求最后围成的面积
按照计算几何惯例先将直线按(x)轴夹角排序,夹角相同保留靠左的
用一个双端队列维护半平面交
维护方法:先保证队列中至少有两个元素
如果队尾两个直线的交点在新入队直线的右侧
那么由于新入队直线与(x)轴夹角一定更大,所以可以直接把队尾弹出
队首同理
但是记住一定要先弹出队尾
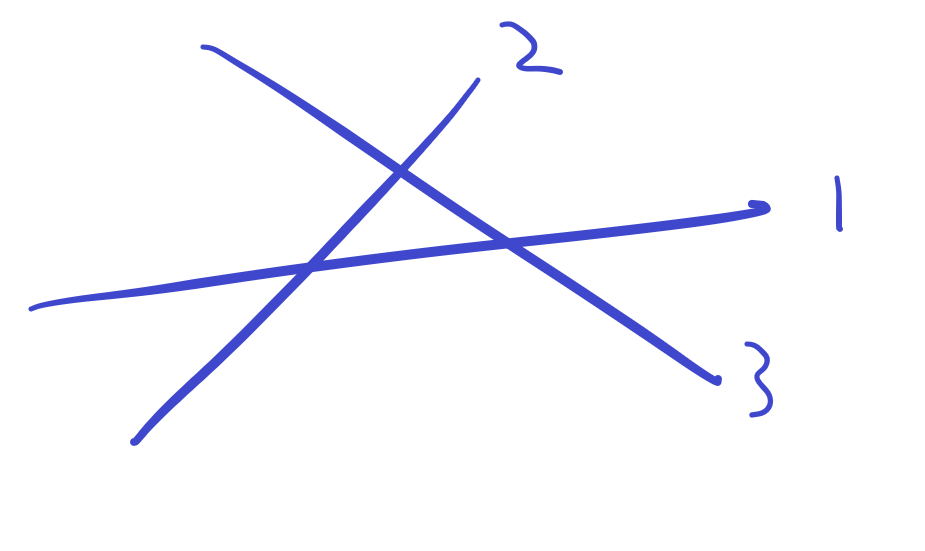
假如图中直线标号是入队顺序,当(3)入队时先判断(1)就会先弹出(1),先判断(2)就会先弹出(2),但显然与队首围成的面积是更小的
最后还要对首尾再检测,防止出现如下情况
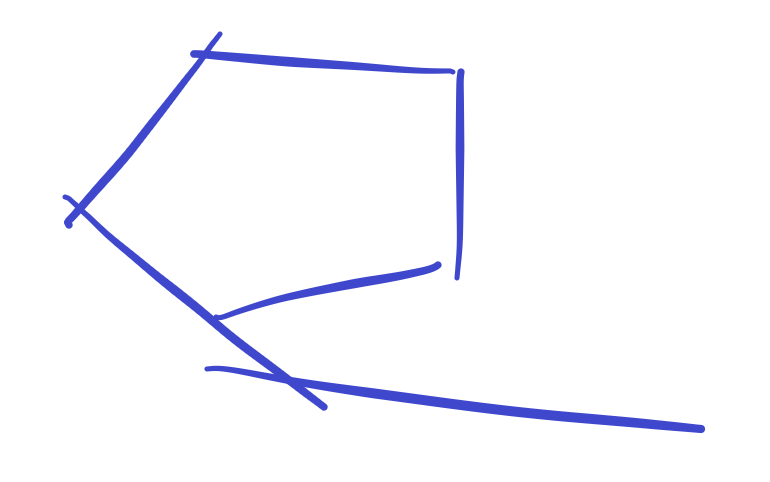
代码细节很多
#include<bits/stdc++.h>
using namespace std;
namespace red{
#define ls(p) (p<<1)
#define rs(p) (p<<1|1)
#define mid ((l+r)>>1)
#define lowbit(i) ((i)&(-i))
#define eps (1e-9)
inline int read()
{
int x=0;char f=0,ch;
for(ch=getchar();(ch<'0'||ch>'9')&&ch!='-';ch=getchar());
if(ch=='-') f=1,ch=getchar();
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
return f?-x:x;
}
const int N=5010;
int n,m,tot,sum,head,tail;
struct node
{
double x,y;
inline double operator ^ (const node &t) const{return x*t.y-y*t.x;}
inline node operator + (const node &t) const{return (node){x+t.x,y+t.y};}
inline node operator - (const node &t) const{return (node){x-t.x,y-t.y};}
inline node operator * (const double &t) const{return (node){x*t,y*t};}
}a[N],c[N];
struct line
{
node a,b;//a是向量起始点,b是以a为原点向量的终点
double k;
line(){}
line(const node &aa,const node &bb):a(aa),b(bb){k=atan2(b.y,b.x);}
inline bool operator < (const line &t) const{return k<t.k;}
}f[N],q[N];
inline double cross(node a,node b,node c){return (b-a)^(c-a);}//跨立
inline node getnode(line A,line B)//面积比例求交点
{
node C=A.a-B.a;//新起点
double t=(B.b^C)/(A.b^B.b);
return A.a+A.b*t;
}
inline int dcmp(double x)
{
if(fabs(x)<eps) return 0;
return x>0?1:-1;
}
inline double are()
{
double are=0;
for(int i=head;i<tail;++i) are+=fabs(cross(c[head],c[i],c[i+1]));
return are/2.0;
}
inline void work()
{
head=tail=1;
q[tail]=f[1];
//c[i]表示a[i]和a[i+1]的交点
for(int i=2;i<=sum;++i)
{
while(head<tail&&(f[i].b^(c[tail-1]-f[i].a))<=eps) --tail;
while(head<tail&&(f[i].b^(c[head]-f[i].a))<=eps) ++head;
q[++tail]=f[i];
if(!dcmp(q[tail].b^q[tail-1].b))//平行保留靠左的
{
--tail;
if(dcmp(q[tail].b^(f[i].a-q[tail].a))==1) q[tail]=f[i];
}
if(head<tail) c[tail-1]=getnode(q[tail-1],q[tail]);
}
while(head<tail&&(q[head].b^(c[tail-1]-q[head].a))<=eps) --tail;//防止最后尾部绕出头部
if(tail-head<=1) return;
c[tail]=getnode(q[head],q[tail]);
}
inline void main()
{
n=read();
for(int i=1;i<=n;++i)
{
m=read();
for(int j=1;j<=m;++j)
{
a[j].x=read(),a[j].y=read();
}
a[0]=a[m];
for(int j=0;j<m;++j)
{
int t=j+1;
f[++sum]=line(a[j],a[t]-a[j]);
}
}
sort(f+1,f+sum+1);
work();
printf("%.3f
",are());
}
}
signed main()
{
red::main();
return 0;
}