R

Given a n*n matrix C _ij (1<=i,j<=n),We want to find a n*n matrix X _ij (1<=i,j<=n),which is 0 or 1.

Besides,X _ij meets the following conditions:

1.X ₁₂+X ₁₃+...X _1n=1
2.X _1n+X _2n+...X _n-1n=1
3.for each i (1<i<n), satisfies ∑X _ki (1<=k<=n)=∑X _ij (1<=j<=n).

For example, if n=4,we can get the following equality:

X ₁₂+X ₁₃+X ₁₄=1
X ₁₄+X ₂₄+X ₃₄=1
X ₁₂+X ₂₂+X ₃₂+X ₄₂=X ₂₁+X ₂₂+X ₂₃+X ₂₄
X ₁₃+X ₂₃+X ₃₃+X ₄₃=X ₃₁+X ₃₂+X ₃₃+X ₃₄

Now ,we want to know the minimum of ∑C _ij*X _ij(1<=i,j<=n) you can get.

Hint

For sample, X ₁₂=X ₂₄=1,all other X _ij is 0.

InputThe input consists of multiple test cases (less than 35 case).
For each test case ,the first line contains one integer n (1<n<=300).
The next n lines, for each lines, each of which contains n integers, illustrating the matrix C, The j-th integer on i-th line is C _ij(0<=C _ij<=100000).OutputFor each case, output the minimum of ∑C _ij*X _ij you can get.
Sample Input

4
1 2 4 10
2 0 1 1
2 2 0 5
6 3 1 2

Sample Output

3

这道题大致一看一脸懵，仔细一看还是懵。。。。。。。。

题意：

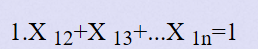
这个条件的意思就是从1这个点只能到到其他点中的一个点，简单一点就是1号点的出度为1

那么这个是n号点，只不过这个是n号点的入度为1

第三个条件就是除了一号点和n号点，其他点的出度等于入度

这个X是题上给出的限制条件，我们要使我们选出来的路符合这两个条件

既然X的值只能为0或1，那么我们只需要求从1到n的最小花费就可以了

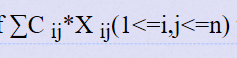
 就是求出来从起点到终点的最小花费，这个样子我们把题目上面输入的数存在邻接矩阵里面直接拿来用，这个矩阵正好满足上面三个条件，所以这是一个结果

但是我们要考虑环的存在，即起点形成一个环，终点n形成一个环，这个样子其他点的出入度为0也满足题意，但是要保证他不是自环，即必须保证有两个点

上代码：

#include<stdio.h>
#include<string.h>
#include<iostream>
#include<algorithm>
#include<queue>
using namespace std;
const int INF=0x3f3f3f3f;
int w[305][305],d[305],dis[305];
queue<int>r;
void spay(int start,int ends)
{
    memset(d,INF,sizeof(d));
    memset(dis,0,sizeof(dis));
    for(int i=1;i<=ends;++i)
    {
        if(i!=start)
        {
            dis[i]=1;
            d[i]=w[start][i];
            r.push(i);
        }
        else
        {
            d[i]=INF;
        }
    }
    while(!r.empty())
    {
        int x=r.front();
        r.pop();
        dis[x]=0;
        for(int i=1;i<=ends;++i)
        {
            if(d[i]>d[x]+w[x][i])
            {
                d[i]=d[x]+w[x][i];
                if(!dis[i])
                {
                    dis[i]=1;
                    r.push(i);
                }
            }
        }
    }
}
int main()
{
    int n;
    while(~scanf("%d",&n))
    {
        memset(w,0,sizeof(w));
        for(int i=1;i<=n;++i)
        {
            for(int j=1;j<=n;++j)
                scanf("%d",&w[i][j]);
        }
        int q1,q2;
        spay(1,n);
        q1=d[n];
        q2=d[1];
        spay(n,n);
        q2+=d[n];
        printf("%d
",min(q1,q2));
    }
    return 0;
}

网搜的代码：

/*
HDU 4370 0 or 1
转换思维的题啊，由一道让人不知如何下手的题，转换为了最短路
基本思路就是把矩阵看做一个图，图中有n个点，1号点出度为1，
n号点入度为1，其它点出度和入度相等，路径长度都是非负数，

等价于一条从1号节点到n号节点的路径，故Xij=1表示需要经
过边(i,j)，代价为Cij。Xij=0表示不经过边(i,j)。注意到Cij非负
且题目要求总代价最小，因此最优答案的路径一定可以对应一条简单路径。

最终，我们直接读入边权的邻接矩阵，跑一次1到n的最短路即可，记最短路为path。

漏了如下的情况B：
从1出发，走一个环（至少经过1个点，即不能
是自环），回到1；从n出发，走一个环（同理），回到n。
也就是1和n点的出度和入度都为1，其它点的出度和入度为0.

由于边权非负，于是两个环对应着两个简单环。

因此我们可以从1出发，找一个最小花费环，记代价为c1,
再从n出发，找一个最小花费环，记代价为c2。
（只需在最短路算法更新权值时多加一条记录即可：if(i==S) cir=min(cir,dis[u]+g[u][i])）

故最终答案为min(path,c1+c2)
*/
/*
本程序用SPFA来完成最短路。
但是由于要计算从出发点出发的闭环的路径长度。
所以要在普通SPFA的基础上做点变化。

就是把dist[start]设为INF。同时一开始并不是让出发点入队，而是让
出发点能够到达的点入队。
*/
#include<stdio.h>
#include<iostream>
#include<string.h>
#include<algorithm>
using namespace std;

const int INF=0x3f3f3f3f;
const int MAXN=330;
int cost[MAXN][MAXN];//保存路径长度的邻接矩阵
int dist[MAXN];
int que[MAXN];//注意队列的循环利用，建成循环队列
bool vis[MAXN];//是否在队列中标记

void SPFA(int start,int n)
{
    int front=0,rear=0;
    for(int v=1;v<=n;v++)//初始化
    {
        if(v==start)//由于要找start的闭环，所以dist[start]设为INF，且不入队
        {
            dist[v]=INF;
            vis[v]=false;
        }
        else if(cost[start][v]!=INF)
        {
            dist[v]=cost[start][v];
            que[rear++]=v;
            vis[v]=true;
        }
        else//即dist[start][v]==INF情况，对本题没有这种情况
        {
            dist[v]=INF;
            vis[v]=false;
        }
    }

    while(front!=rear)//注意这个条件是不等，因为是循环队列
    {
        int u=que[front++];
        for(int v=1;v<=n;v++)
        {
            if(dist[v]>dist[u]+cost[u][v])
            {
                dist[v]=dist[u]+cost[u][v];
                if(!vis[v])//不在队列
                {
                    vis[v]=true;
                    que[rear++]=v;
                    if(rear>=MAXN) rear=0;//循环队列
                }
            }
        }
        vis[u]=false;
        if(front>=MAXN)front=0;
    }

}
int main()
{
    //freopen("in.txt","r",stdin);
    //freopen("out.txt","w",stdout);
    int n;
    while(scanf("%d",&n)!=EOF)
    {
        for(int i=1;i<=n;i++)
          for(int j=1;j<=n;j++)
            scanf("%d",&cost[i][j]);
        SPFA(1,n);
        int ans=dist[n];//1到n的最短路
        int loop1=dist[1];//1的闭环长度
        SPFA(n,n);
        int loopn=dist[n];//n的闭环长度
        ans=min(ans,loop1+loopn);
        printf("%d
",ans);
    }
    return 0;
}