（二维）判断一个点是否在凸多边形内 & 已知圆上三点求圆心和半径

一、判断一个点是否在凸多边形内 

根据向量叉乘的右手定则：

右手除姆指外的四指合并，姆指与其他四指垂直，四指由A向量的方向握向B向量的方向，这时姆指的指向就是A，B向量向量积的方向。就是说，AB向量积的方向垂直于AB向量确定的平面。如下图所示：

根据右手定则判断点是否在凸多边形内原理（原文链接：https://blog.csdn.net/qq_35465996/article/details/100054558）：

二维向量叉乘，最终会得到一个(0,0,z)的向量，z的正负方向符合右手定则。已知凸多边形质心在多边形内，如果一点在凸多边形内部，则这个点一定属于质心与多边形边的内部；反之，点拘于图形外。
如图，做点至多边形顶点构成多条向量，按照某个方向（顺时针/逆时针），则必然存在相邻向量的向量积彼此反向，即点在图形外，如p b pbpbXp c pcpc与p c pcpcXp d pdpd，根据右手定则，知叉乘结果必然相反。

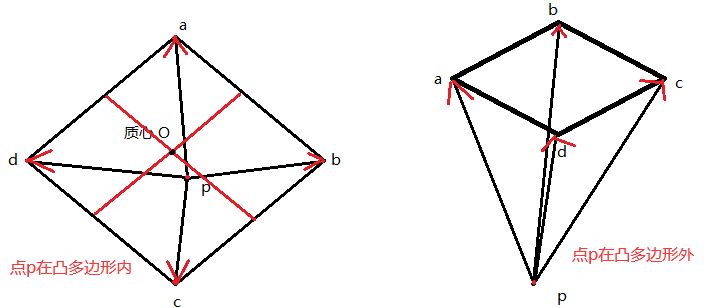
将图多边形所有点和点p连线，按照顺时针/逆时针，相邻向量做叉乘，得到的相邻结果里面有异号的，即为外点。否则点在凸多边形内

C++代码：

#include <iostream>
#include <array>
#include <vector>

using namespace std;
using vector2d = array<double, 2>;

//向量积
double crossProduct(vector2d &p1, vector2d &p2)
{
    return (p1[0]*p2[1]-p2[0]*p1[1]);
}

//判定点在凸多边形内 
bool pointInConvexPolygon(vector2d p, vector<vector2d>& polygon)
{
    int i, iNext, i2Next;
    double preCross, nextCross;
    vector2d v1, v2, v3;
    int polySize= polygon.size();
    
    if(polySize < 3)
    {
        return false;
    }
    for(i = 0; i < polySize; i++)
    {
        iNext = (i + 1) %  polySize;
        i2Next = (iNext + 1) % polySize;
        
        //注意v1, v2, v3最好归一化一下，防止图像坐标过大，导致叉乘结果溢出
        v1={polygon[i][0]-p[0], polygon[i][1]-p[1]};
        v2={polygon[iNext][0]-p[0], polygon[iNext][1]-p[1]};
        preCross = crossProduct(v1,v2);
        
        v3={polygon[i2Next][0]-p[0], polygon[i2Next][1]-p[1]};
        nextCross = crossProduct(v2,v3);
        
        if(preCross * nextCross < 0)
        {
            return false;
        }
    }
    
    return true;
}
    
int main()
{
    vector<vector2d> poly{{0,0}, {0, 2}, {2, 0}};
    vector2d p{4, 4};
    
    if(pointInConvexPolygon(p, poly))
    {
        cout<<"this point is in the polygon.
";
    }
    else
    {
        cout<<"this point is not in the polygon.
";
    }
    
    return 0;
}

二、已知圆上三点求圆心和半径

原文：https://blog.csdn.net/weixin_44957370/article/details/116455334

原理：圆上的任意两点的连线称作弦，弦的中垂线必过圆心，取三点组成的两条弦的中垂线的交点，即为圆心，再通过圆心求半径.

其中三点坐标为 (dx1,dy1) (dx2,dy2) (dx3,dy3)

h1 h2 是弦的的中垂线的 斜率 x y 为圆心坐标 radius 为半径

代码：

double midx1,midy1,midx2,midy2;
double h1,h2;
 
//求前两个点的中心点
midx1 = (dx1 + dx2) / 2;
midy1 = (dy1 + dy2) / 2;
 
//两条垂线斜率乘积为 -1
h1 = - (dx2 - dx1) / (dy2 - dy1);
 
//求后两个点的中心点
midx2 = (dx2 + dx3) / 2;
midy2 = (dy2 + dy3) / 2;
 
//两条垂线斜率乘积为 -1
h2 = - (dx3 - dx2) / (dy3 - dy2);
 
//对应的垂线表示为
 
// y = h1(x - midx1) + midy1;
// y = h2(x - midx2) + midy2;
 
//转化得
double x = (midy2 - midy1 + midx1*h1 - midx2*h2) / (h1 - h2);
double y = h1 * ( x - midx1) + midy1;
 
double radius = _hypot(fabs(x - dx1), fabs(y - dy1));