直线和圆求交点（向量法）

原文链接：https://blog.csdn.net/fengkeyleaf/article/details/117692135

如果看过上一节的直线交点，那么这里求直线和圆的交点思路是非常相似的：

1、用直线到圆心的距离和半径相比，判断是否和圆有交点；
2、求出圆心在直线上面的投影点(projectPoint)；
3、算出直线的单位向量e；
4、求出一侧交点(Intersection)到projectPoint的长度(sideLength)；
5、求出sideLength和这侧端点到projectPoint距离的比例(ratio)；
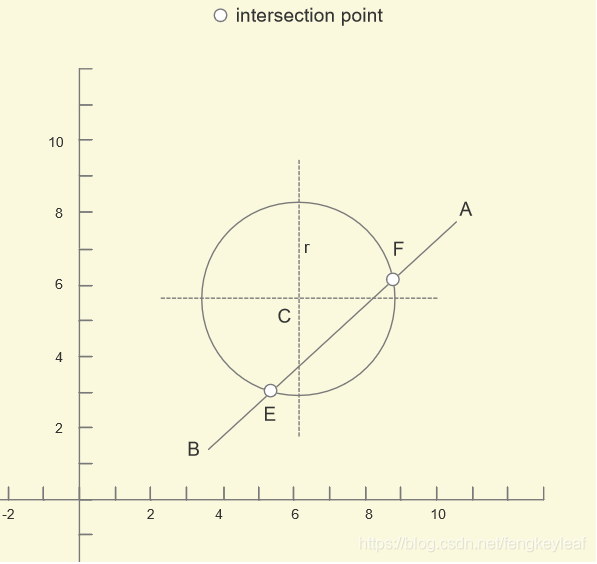
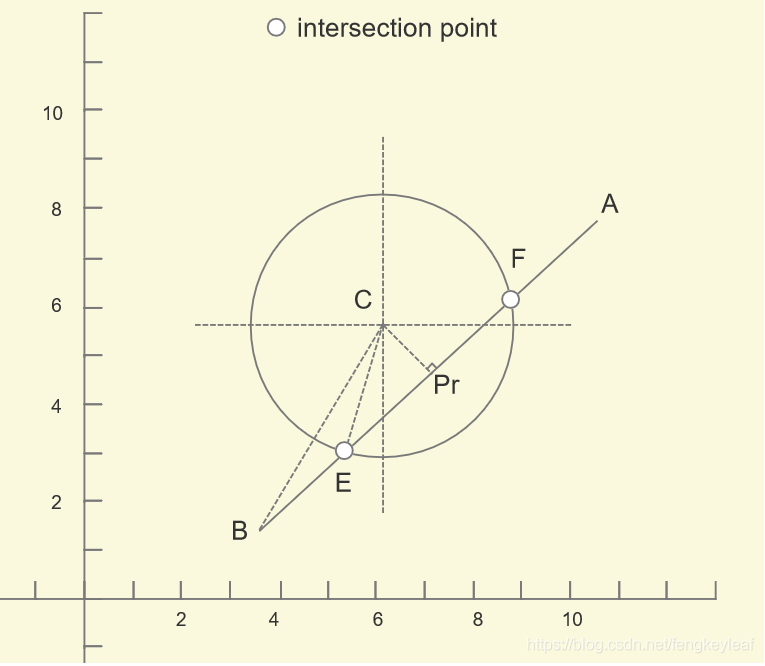
6、projectPoint +/- ratio * e = 两侧交点；

同样，我们还是通过一个图例来讲解。我们给定圆，圆心为C，半径为r，和直线AB，以及它们两个交点E和F：

 

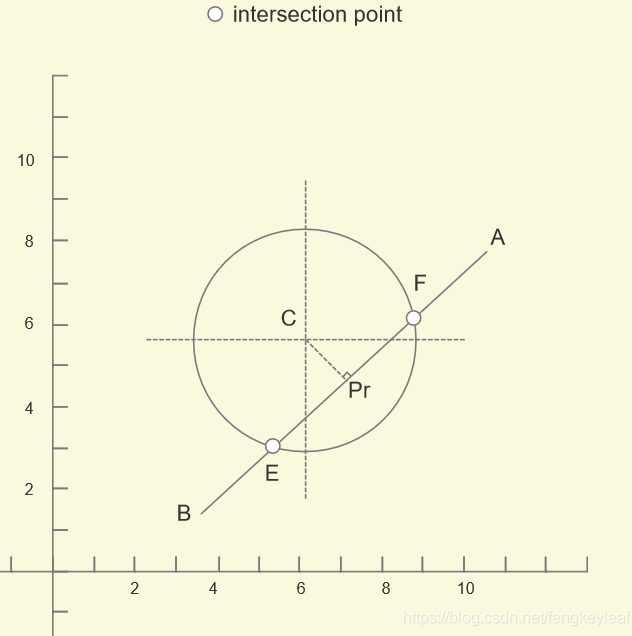
现在我们以求交点E为例来进行讲解。使用求直线交点的思路，如果我们首先会考虑从B出发，求得BE和某个向量的比例，即可通过B来计算交点E，但是这样不是很好找比例，所以我们换一种思路，先求C在直线AB上面的投影Pr：

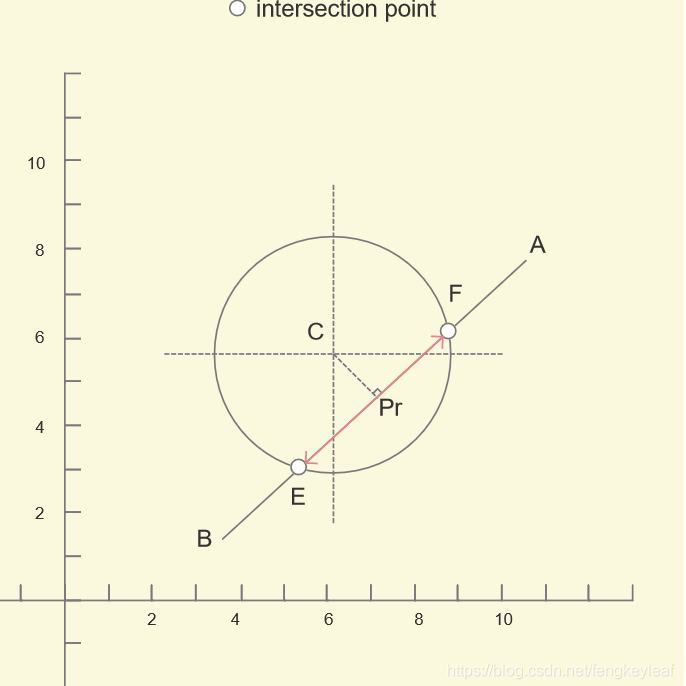
 那么显然，我们可以得到一组向量的比例关系：BPr 和 EPr（加粗表示向量），因为圆和直线可能有两个交点，分别位于Pr的两边，所以我们选Pr作为起点求交点比较方便：

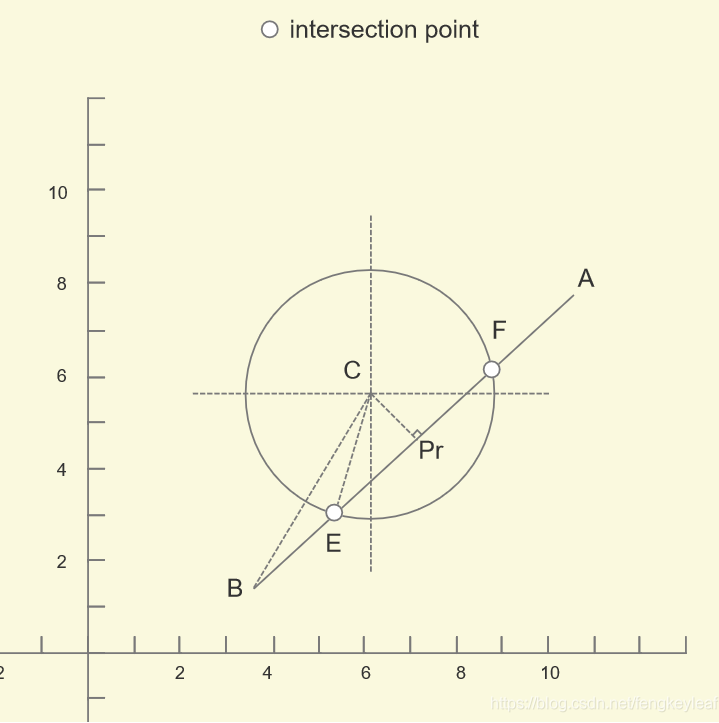
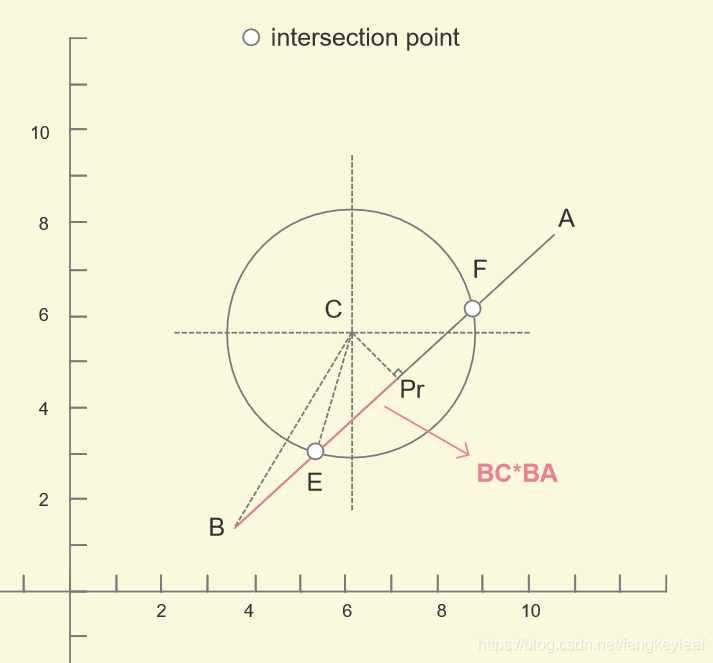
有了这个比例关系(ratio)，我们只要知道BA的单位向量e，用 ratio * e，就可以得到EPr和PrF。因为根据垂径定理1，|EPr| = |PrF|。所以我们先假设求得了Pr，那么|EPr|和|BPr|怎么求呢？我们连接BC和EC看看：

从图中可知，|EPr|不难求，直角三角形CEPr可用勾股定理求得；那么|BPr|呢？现在又需要向量的帮助了，大家还记得向量得点积么？两个向量a和b的点积表示a在b上面的投影，所以|BPr| = BC * BPr。那么到现在，还剩下两个问题就能解决交点了：1）如何求C在直线AB上面的投影；2）如何求C到直线AB的距离；

2.2 点在直线上面的投影
在文章开头，我们曾经提到下面的思路去求解交点：

现在我们以求交点E为例来进行讲解。使用求直线交点的思路，如果我们首先会考虑从B出发，求得BE和某个向量的比例，即可通过B来计算交点E

虽然这个方法求交点不是很好，但是我们可以用它来求解点在直线上面的投影。还是上面圆的图例：

 所以我们只需要求出BPr和BA的比例关系，即可以求解Pr，而且|BPr|可以BC和BA的点积来求得，因为两者点积是BC在BA上面的投影，通过这样，我们就能求得比例关系了，如下图所示：

2.3 点到直线的距离

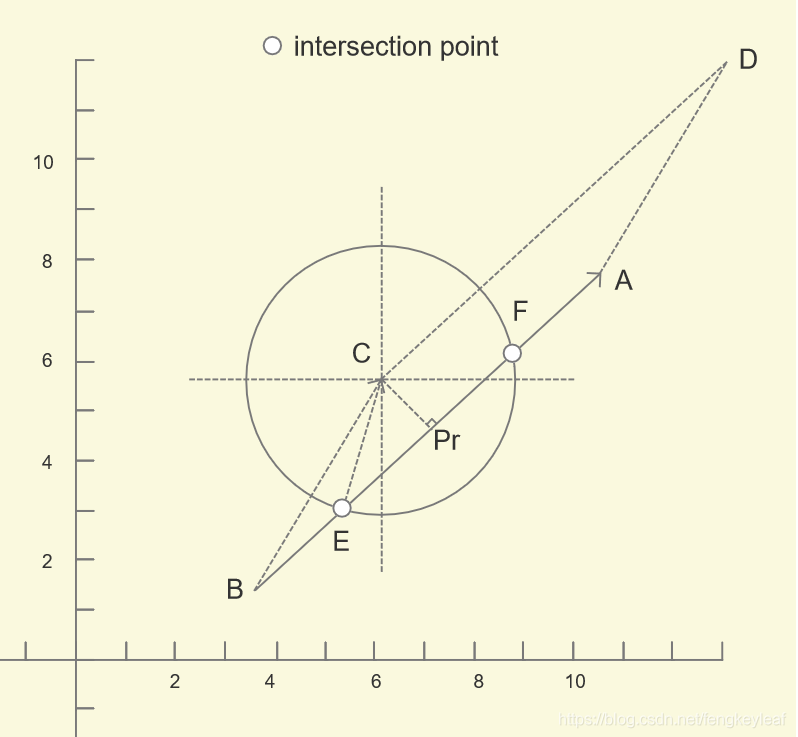
点到直线的距离，我们可以看成平行四边形的高，然后用叉积来求得，还是刚才的图例：

 我们看到C到AB的距离(CPr)其实平行四边形BADC的高，所以我们可以利用BC和BA的叉积来求解。

代码来源于https://blog.csdn.net/qq_40998706/article/details/87521165：

这是一个题目：

#include<stdio.h>
#include<iostream>
#include<cmath>
#include<assert.h>
using namespace std;

#define EPS (1e-10)
#define equals(a, b) (fabs((a) - (b)) < EPS)

class Point {//Point类，点 
    public:
        double x, y;
        
        Point(double x = 0, double y = 0): x(x), y(y) {}

        Point operator + (Point p) { return Point(x + p.x, y + p.y); }
        Point operator - (Point p) { return Point(x - p.x, y - p.y); }
        Point operator * (double a) { return Point(a * x, a * y); }
        Point operator / (double a) { return Point(x / a, y / a); }

        double abs() { return sqrt(norm()); }
        double norm() { return x * x + y * y; }
        
        bool operator < (const Point &p) const {
            return x != p.x ? x < p.x : y < p.y;
        }

        bool operator == (const Point &p) const {
            return fabs(x - p.x) < EPS && fabs(y - p.y) < EPS;
        }
};

typedef Point Vector;//Vector类，向量 

struct Segment{//Segment 线段 
    Point p1, p2;
};

typedef Segment Line;

class Circle {//Circle 圆 
    public:
        Point c;
        double r;
        Circle(Point c = Point(), double r = 0.0): c(c), r(r) {}
};

double dot(Vector a, Vector b) {//内积 
    return a.x * b.x + a.y * b.y;
}

double cross(Vector a, Vector b) {//外积 
    return a.x*b.y - a.y*b.x;
}

Point project(Segment s, Point p) {//投影 对于给定的三个点p1、p2、p，从点p向通过
//p1、p2的直线引一条垂线，求垂足x的坐标。（点p在直线p1p2上的投影） 
    Vector base = s.p2 - s.p1;
    double r = dot(p - s.p1, base) / base.norm();
    return s.p1 + base * r;
} 

double getDistanceLP(Line l, Point p) {//直线l和点p的距离
    return abs(cross(l.p2 - l.p1, p - l.p1) / (l.p2 - l.p1).abs() );
}

bool intersect(Circle c, Line l) {
    if(getDistanceLP(l, c.c) > c.r) {
        return false;
    } else {
        return true;
    }
}
Point getCrossPoint(Segment s1, Segment s2) {
    Vector base = s2.p2 - s2.p1;
    double d1 = abs(cross(base, s1.p1 - s2.p1));
    double d2 = abs(cross(base, s1.p2 - s2.p1));
    double t = d1 / (d1 + d2);
    return s1.p1 + (s1.p2 - s1.p1) * t;
}

pair<Point, Point> getCrossPoints(Circle c, Line l) {
    assert(intersect(c, l));
    Vector pr = project(l, c.c);
    Vector e = (l.p2 - l.p1) / (l.p2 - l.p1).abs();
    double base = sqrt(c.r * c.r - (pr - c.c).norm() );
    return make_pair(pr + e * base, pr - e * base);
}

int main(){
    Circle c;
    cin>>c.c.x>>c.c.y>>c.r;
    
    int q;
    cin>>q;
    
    Line l;
    pair<Point, Point> p;
    
    while(q--){
        cin>>l.p1.x>>l.p1.y>>l.p2.x>>l.p2.y;
        p = getCrossPoints(c, l);
        if(p.first.x < p.second.x || (p.first.x == p.second.x && p.first.y <= p.second.y) ) {
            printf("%.6f %.6f %.6f %.6f
", p.first.x, p.first.y, p.second.x, p.second.y);
        } else {
            printf("%.6f %.6f %.6f %.6f
", p.second.x, p.second.y, p.first.x, p.first.y);
        }
    }
}