POJ 1456 Supermarket （贪心+并查集）

Supermarket

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 7501		Accepted: 3148

Description

A supermarket has a set Prod of products on sale. It earns a profit px for each product x∈Prod sold by a deadline dx that is measured as an integral number of time units starting from the moment the sale begins. Each product takes precisely one unit of time for being sold. A selling schedule is an ordered subset of products Sell ≤ Prod such that the selling of each product x∈Sell, according to the ordering of Sell, completes before the deadline dx or just when dx expires. The profit of the selling schedule is Profit(Sell)=Σ_x∈Sellpx. An optimal selling schedule is a schedule with a maximum profit. 
For example, consider the products Prod={a,b,c,d} with (pa,da)=(50,2), (pb,db)=(10,1), (pc,dc)=(20,2), and (pd,dd)=(30,1). The possible selling schedules are listed in table 1. For instance, the schedule Sell={d,a} shows that the selling of product d starts at time 0 and ends at time 1, while the selling of product a starts at time 1 and ends at time 2. Each of these products is sold by its deadline. Sell is the optimal schedule and its profit is 80.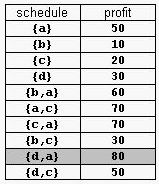 

Write a program that reads sets of products from an input text file and computes the profit of an optimal selling schedule for each set of products. 

Input

A set of products starts with an integer 0 <= n <= 10000, which is the number of products in the set, and continues with n pairs pi di of integers, 1 <= pi <= 10000 and 1 <= di <= 10000, that designate the profit and the selling deadline of the i-th product. White spaces can occur freely in input. Input data terminate with an end of file and are guaranteed correct.

Output

For each set of products, the program prints on the standard output the profit of an optimal selling schedule for the set. Each result is printed from the beginning of a separate line.

Sample Input

4  50 2  10 1   20 2   30 1

7  20 1   2 1   10 3  100 2   8 2
   5 20  50 10

Sample Output

80
185

Hint

The sample input contains two product sets. The first set encodes the products from table 1. The second set is for 7 products. The profit of an optimal schedule for these products is 185.

Source

Southeastern Europe 2003

 

 

 

 

 

这里其实用贪心做，并查集只是用来作为工具，使得速度更加快。

题目大意是买卖N件东西，每件东西都有个截止时间，在截止时间之前买都可以，而每个单位时间只能买一件。问最大获利。

如果购买不冲突，那么全部买下来就可以了。存在冲突，就需要取舍。显然在冲突的时候我们选择价格高的更优，如此就可以用贪心的算法。先将物品按照价格从高到底的顺序排列，购买一个就在时间点上做一个标记，只要不冲突就可以购买。 如何快速找到第一个不冲突的时间点呢，个人感觉使用并查集很好得解决了这个问题。 这里并查集的作用类似于链表指针，压缩的过程就是删掉节点的过程。从而在O(1)的时间内找到那个不冲突的点。

 

 

/*
POJ 1456
贪心处理。
按照获利p从大到小排序。
处理的时候选择最后的一个不冲突点。

用并查集实现链表的作用，快速找到不冲突点
*/
#include <stdio.h>
#include <string.h>
#include <iostream>
#include <algorithm>
using namespace std;
const int MAXN=10010;
int F[MAXN];
struct Node
{
    int p,d;
}node[MAXN];
bool cmp(Node a,Node b)//按p从大到小排序。d没有关系
{
    return a.p>b.p;
}
int find(int x)
{
    if(F[x]==-1)return x;
    return F[x]=find(F[x]);
}
int main()
{
    int n;
    while(scanf("%d",&n)==1)
    {
        memset(F,-1,sizeof(F));
        for(int i=0;i<n;i++)
          scanf("%d%d",&node[i].p,&node[i].d);
        sort(node,node+n,cmp);
        int ans=0;
        for(int i=0;i<n;i++)
        {
            int t=find(node[i].d);
            if(t>0)
            {
                ans+=node[i].p;
                F[t]=t-1;
            }
        }
        printf("%d\n",ans);
    }
    return 0;
}