分解：
设有关系模式R(U)和R1(U1), R2(U2), …, Rk(Uk)，其中U={A1, A2, …, An}，Ui ⊆ U(i=1,2,…, k)，且U＝U1+U2+ …+Uk。令ρ={R1(U1), R2(U2), …, Rk(Uk)}，ρ为R(U)的一个分解，也称为数据库模式，有时也称为模式集。
无损连接：
F是R(U)满足的一个函数依赖集，将R(U)分解成关系模式ρ={R1(U1)，R2(U2) … Rk(Uk)}，U＝U1+U2+…+Uk。如果对R(U)中满足F的每一个具体关系r都有：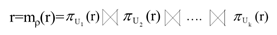
则称这个分解ρ相对于F 具有无损连接性，简称ρ为无损连接分解，即r为它自己在Ui上投影的自然连接。
无损连接的测试：
【设关系模式R(A,B,C,D,E)分解为ρ={R1(A,D), R2(A,B), R3(B,E), B4(C,D,E), R5(A,E)}，其函数依赖集是F={A→C, B→C, C→D, DE→C, CE→A}】
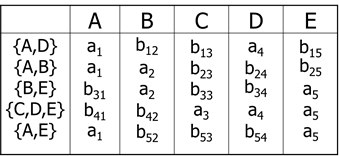
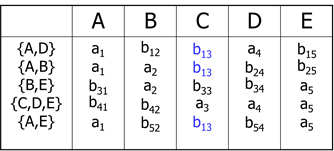
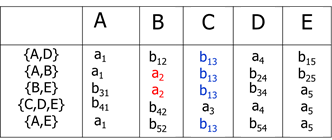
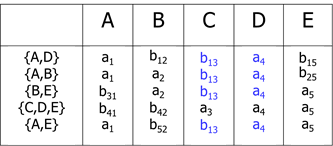
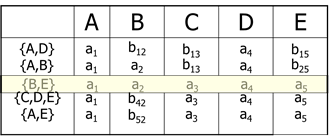
如果R(U) 的分解为ρ＝{ Rl(U1)，R2(U2)}，其中U=U1∪U2，F为R(U)所满足的函数依赖集合，则分解ρ是无损连接的充分必要条件为 ( U1∩U2)→(U1-U2) 或者(U1∩U2)→(U2-U1)成立。
当模式R分解成两个关系模式Rl(U1)和R2(U2)时，如果其公共属性能函数决定U1或U2中的其它属性，这样的分解就是无损连接的。
【设关系模式R(A,B,C)，F＝{A→B}】
R1＝{Rl(A,B)，R2(A,C)}是无损连接的，而R2＝{Rl(A,B)，R3(B,C)}不是无损连接。
函数依赖：
设关系模式R(U)的一个分解ρ={R1(U1),R2(U2), …, Rk(Uk)}，F是R(U)满足的函数依赖集，且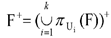
函数依赖的测试：
检验一个分解是否保持函数 依赖，就是检验函数依赖集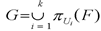
是否覆盖函数依赖集F
设F是属性集U上的函数依赖集，Z是U上的一个子集，F在Z上的一个投影用ΠZ(F)表示，定义为：
ΠZ(F)＝{X→Y | (X→Y)∈F+且XY⊆Z}
【设关系模式R(A,B,C,D)，F={A→B, B→C,C→D,D→A}，R的一个分解ρ={R1(A,B),R2(B,C), R3(C,D)}】
由函数依赖集F和分解ρ可知：
F1=Π{A,B}(F)={A→B，B→A}，F2=Π{B,C} (F)={B→C，C→B}，F3=Π{C,D} (F)={C→D，D→C}
G={A→B, B→A,B→C, C→B,C→D,D→C}，F=F-G={D→A},Result=True
对于函数依赖D→A，即令X={D},Y={A}，有X→Y，F=F-{D→A}=ф
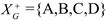
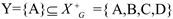
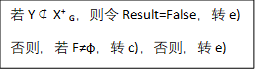
由于Result=True，所以关系模式R的分解ρ保持函数依赖F。
性质
-
若要求分解保持函数依赖，那么模式分解总可以达到3NF，但不一定能达到BCNF。
-
若要求分解既保持函数依赖，又具有无损连接性，可以达到3NF，但不一定能达到BCNF。
-
若要求分解具有无损连接性，那一定可达到4NF。
将一个关系模式R分解成3NF模式，且既保持函数依赖又具有无损连接性的算法：
-
求出函数依赖集F的最小覆盖并仍记为F, 令ρ=ф
-
若F中有函数依赖X→Y,满足XY=U, 则ρ＝ρ∪{R(U)}，则转f)。
-
如果U中某些属性U1在F的所有函数依赖的左部和右部都不出现，则把这些属性构成一个关系模式R(U1)，然后把这些属性从U中去掉，剩余的属性仍记为U，令ρ＝ρ∪{R(U)}。
-
对F中所有以X为左部的函数依赖X→Y1,X→Y2,…,X→Yk，构成关系模式 R(XY1Y2…Yk)， 其函数依赖集为 { X→Y1,X→Y2,…,X→Yk}，令ρ=ρ∪{R(XY1Y2…Y1)} ，F=F-{X→Y1, X→Y2, …, X→Yk}。
-
若F= ф转f)，否则转d)
-
输出
设ρ＝{R1(U1), R2(U2),…, Rk(Uk)}是由上述算法得到的一个分解。设X是R(U)的一个候选键，若存在某个Ui 使X⊆Ui，则令т=ρ，否则 令т=ρ∪{Rx(X)}。
则 т 是R的一个分解，т 中所有模式都是3NF，且这个分解具有无损连接和保持函数依赖两个特性。
【设关系模式R(U),它满足的函数依赖集 F={A→B,AE→P, CD→A,CE→D, BC→D}已是最小函数依赖集】
ρ={R1(A,B), R2(A,E,P), R3(C,D,A), R4(C,E,D), R5(B,C,D)}
由于R的一个候选键属性集是{C,E}⊆U4={C,E,D}