一、CAP 理论
CAP 理论关注的是在绝对情况下,在工程上,可用性和一致性并不是完全对立的,我们关注的往往是如何在保持相对一致性的前提下,提高系统的可用性。
CAP 理论中是忽略网络延迟的,也就是当事务提交时,节点间的数据复制一定是需要花费时间的。即使是同一个机房,从节点 A 复制到节点 B,由于现实中网络不是实时的,所以总会有一定的时间不一致。
CP架构:
我们熟悉的 ZooKeeper,就是采用了 CP 一致性,ZooKeeper 是一个分布式的服务框架,主要用来解决分布式集群中应用系统的协调和一致性问题。其核心算法是 Zab,所有设计都是为了一致性。在
CAP 模型中,ZooKeeper 是 CP,这意味着面对网络分区时,为了保持一致性,它是不可用的。
AP 架构:
对于 AP 来说,放弃强一致性,追求分区容错性和可用性,这是很多分布式系统设计时的选择, Base理论也是根据 AP 来扩展的。和 ZooKeeper 相对的是 Eureka,Eureka 是 Spring Cloud 微服务技术栈中的服务发现组件,Eureka 的各个节点都是平等的,几个节点挂掉不影响正常节点的工作,剩余的节点依然可以提供注册和查询服务,只要有一台 Eureka 还在,就能保证注册服务可用,只不过查到的信息可能不是最新的版本,不保证一致性。
二、BASE理论
Base 是三个短语的简写,即基本可用(Basically Available)、软状态(Soft State)和最终一致性(Eventually Consistent)。
Base 理论的核心思想是最终一致性,即使无法做到强一致性(Strong Consistency),但每个应用都可以根据自身的业务特点,采用适当的方式来使系统达到最终一致性(Eventual Consistency)。
在系统设计中,最终一致性实现的时间取决于网络延时、系统负载、不同的存储选型、不同数据复制方案设计等因素。

三、 2PC/XA,TCC
TCC 对比 2PC 两阶段提交
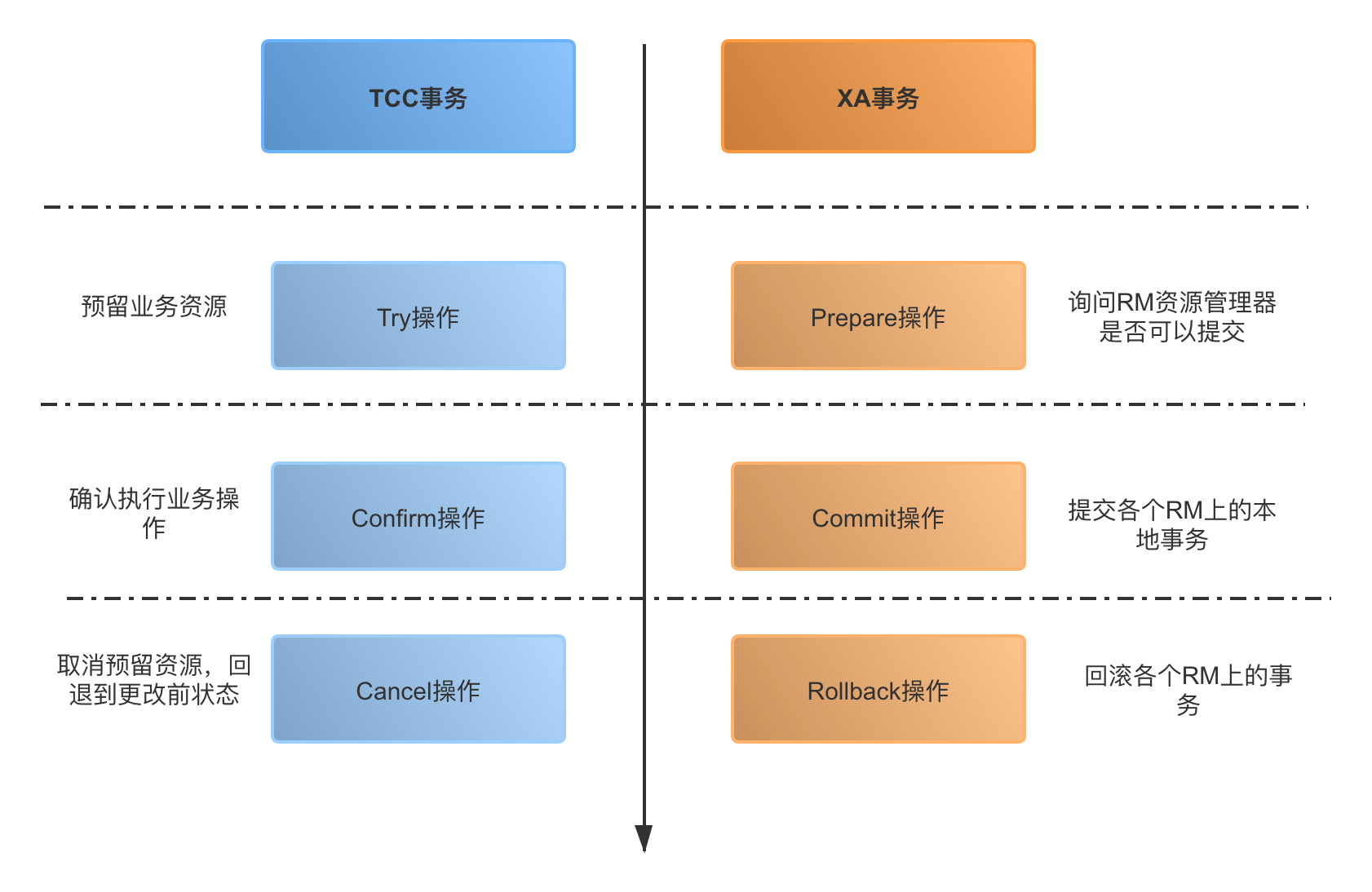
第一阶段
在 XA 事务中,各个 RM 准备提交各自的事务分支,事实上就是准备提交资源的更新操作(insert、delete、update 等);而在 TCC 中,是主业务操作请求各个子业务服务预留资源。
第二阶段
XA 事务根据第一阶段每个 RM 是否都 prepare 成功,判断是要提交还是回滚。如果都 prepare 成功,那么就 commit 每个事务分支,反之则 rollback 每个事务分支。
在 TCC 中,如果在第一阶段所有业务资源都预留成功,那么进入 Confirm 步骤,提交各个子业务服务,完成实际的业务处理,否则进入 Cancel 步骤,取消资源预留请求。
与 2PC/XA 两阶段提交的区别
2PC/XA 是数据库或者存储资源层面的事务,实现的是强一致性,在两阶段提交的整个过程中,一直会持有数据库的锁。
TCC 关注业务层的正确提交和回滚,在 Try 阶段不涉及加锁,是业务层的分布式事务,关注最终一致性,不会一直持有各个业务资源的锁。
TCC 的核心思想是针对每个业务操作,都要添加一个与其对应的确认和补偿操作,同时把相关的处理,从数据库转移到业务中,以此实现跨数据库的事务。
应用 TCC 的优缺点
实际开发中,TCC 的本质是把数据库的二阶段提交上升到微服务来实现,从而避免数据库二阶段中长事务引起的低性能风险。
所以说,TCC 解决了跨服务的业务操作原子性问题,比如下订单减库存,多渠道组合支付等场景,通过 TCC 对业务进行拆解,可以让应用自己定义数据库操作的粒度,可以降低锁冲突,提高系统的业务吞吐量。
TCC 的不足主要体现在对微服务的侵入性强,TCC 需要对业务系统进行改造,业务逻辑的每个分支都需要实现 try、Confirm、Cancel 三个操作,并且 Confirm、Cancel 必须保证幂等。
另外 TCC 的事务管理器要记录事务日志,也会损耗一定的性能。