前提
void X_Sort ( ElementType A[], int N )
大多数情况下,为简单起见,讨论从小大的整数排序
N是正整数
只讨论基于比较的排序(> = < 有定义)
只讨论内部排序
稳定性:任意两个相等的数据,排序前后的相对位置不发生改变
1.冒泡排序
 (从小到大排序)
(从小到大排序)
物理意义:大泡泡往下沉,小泡泡往上冒
每次比较相邻两个泡泡,符合条件,交换位置,每一轮比较完,最大的泡泡沉到最底下。
最好情况:顺序T = O( N )
最坏情况:逆序T = O( N^2 )
稳定

1 #include <stdio.h> 2 3 typedef int ElementType; 4 5 void BubbleSort(ElementType A[], int N) 6 { 7 for(int P = N-1; P >= 0; P--) { 8 int flag = 0; 9 for(int i = 0; i < P; i++) { 10 if( A[i] > A[i+1] ) { 11 ElementType temp = A[i]; //swap A[i] A[i+1] 12 A[i] = A[i+1]; 13 A[i+1] = temp; 14 flag = 1; 15 } 16 } 17 if(flag == 0) 18 break; 19 } 20 } 21 22 int main() 23 { 24 int a[] = {34,8,64,51,32,21}; 25 BubbleSort(a,6); 26 for(int i = 0; i < 6; i++) 27 printf("%d ",a[i]); 28 29 return 0; 30 }
2.插入排序

(从小到大排序)
和打扑克摸牌差不多,每次摸牌从最后往前依次进行比较,需插入的牌小,往前比较,找到合适位置插入。
最好情况:顺序T = O( N )
最坏情况:逆序T = O( N^2 )
稳定

1 #include <stdio.h> 2 3 typedef int ElementType; 4 5 void InsertionSort(ElementType A[], int N) 6 { 7 int i; 8 for (int P = 1; P < N; P++ ) { 9 ElementType temp = A[P]; //取出未排序序列中的第一个元素 10 for (i = P; i > 0 && A[i-1] > temp; i-- ) 11 A[i] = A[i-1]; //依次与已排序序列中元素比较并右移 12 A[i] = temp; 13 } 14 } 15 16 int main() 17 { 18 int a[] = {34,8,64,51,32,21}; 19 InsertionSort(a,6); 20 for(int i = 0; i < 6; i++) 21 printf("%d ",a[i]); 22 return 0; 23 }
3.希尔排序
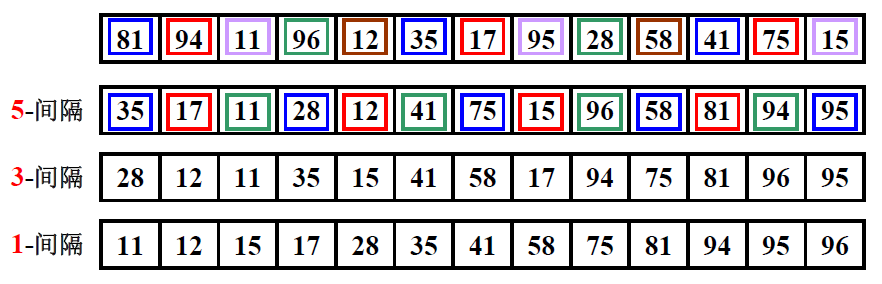
每5 3 1间隔数进行插入排序。
5 3 1成为增量序列。
定义增量序列DM > DM-1 > … > D1 = 1
对每个Dk 进行“Dk-间隔”排序( k = M, M-1, … 1 )
“Dk-间隔”有序的序列,在执行“Dk-1-间隔”排序后,仍然是“Dk-间隔”有序的
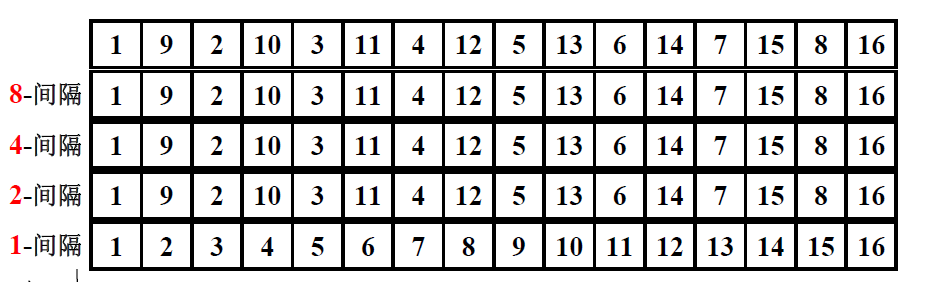
原始希尔排序DM = [N / 2]向下取整 , Dk = [D(k+1) / 2]向下取整
最坏情况: T =Ο( N^2 ) 不稳定
增量元素不互质,则小增量可能根本不起作用。
更多增量序列
Hibbard 增量序列
Dk = 2^k – 1 — 相邻元素互质
最坏情况: T = O ( N^ 3/2 )
猜想:Tavg = O ( N^ 5/4 )
Sedgewick增量序列
{1, 5, 19, 41, 109, … }
9*4^i – 9*2^i + 1 或4^i – 3*2^i + 1
猜想:Tavg = O ( N^ 7/6 ),Tworst = O ( N^ 4/3 )

1 #include <stdio.h> 2 3 typedef int ElementType; 4 5 /* 原始希尔排序 */ 6 void Shell_Sort(ElementType A[], int N) 7 { 8 int i; 9 for(int D = N/2; D > 0; D/=2) { 10 for(int P = D; P < N; P++) { 11 ElementType temp = A[P]; 12 for(i = P; i >= D && A[i-D]>temp; i-=D) 13 A[i] = A[i-D]; 14 A[i] = temp; 15 } 16 } 17 } 18 19 /* 希尔排序 - 用Sedgewick增量序列 */ 20 void ShellSort(ElementType A[], int N) 21 { 22 int Si, i; 23 /* 这里只列出一小部分增量 */ 24 int Sedgewick[] = {929, 505, 209, 109, 41, 19, 5, 1, 0}; 25 26 for ( Si = 0; Sedgewick[Si] >= N; Si++ ) 27 ; /* 初始的增量Sedgewick[Si]不能超过待排序列长度 */ 28 29 for (int D = Sedgewick[Si]; D > 0; D = Sedgewick[++Si]) 30 for (int P = D; P < N; P++ ) { //插入排序 31 ElementType temp = A[P]; 32 for(i = P; i >= D && A[i-D]>temp; i-=D) 33 A[i] = A[i-D]; 34 A[i] = temp; 35 } 36 } 37 38 int main() 39 { 40 int a[] = {34,8,64,51,32,21}; 41 Shell_Sort(a,6); 42 ShellSort(a,6); 43 for(int i = 0; i < 6; i++) 44 printf("%d ",a[i]); 45 return 0; 46 }
4.堆排序
(从小到大排序)
首先将堆调整为最大堆,堆顶元素为数组最大元素在A[0]位置,与A[N]交换位置。找到最大元素,将其放在最后。
再调整为最大堆,且堆的大小-1,为N-1。依次执行。
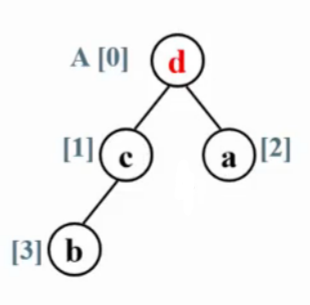
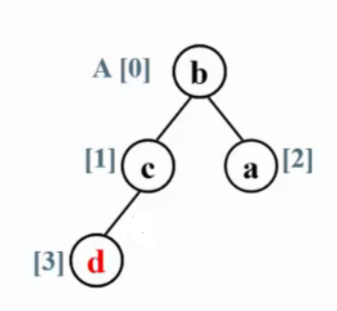
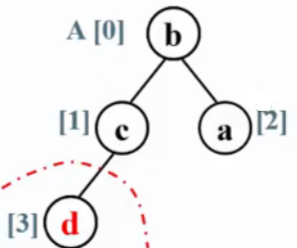

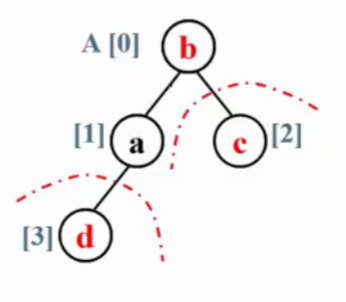
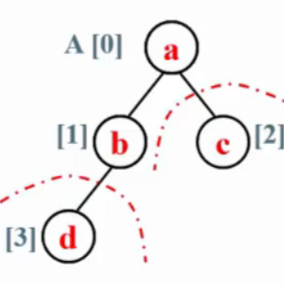
定理:堆排序处理N个不同元素的随机排列的平均比较次数是2N logN - O(Nlog logN) 。 不稳定
虽然堆排序给出最佳平均时间复杂度,但实际效果不如用Sedgewick增量序列的希尔排序。

1 #include <stdio.h> 2 3 typedef int ElementType; 4 5 void Swap( ElementType *a, ElementType *b ) 6 { 7 ElementType t = *a; 8 *a = *b; 9 *b = t; 10 } 11 /* 改编PercDown( MaxHeap H, int p )*/ 12 void PercDown( ElementType A[], int p, int N ) 13 { 14 /* 将N个元素的数组中以A[p]为根的子堆调整为最大堆 */ 15 int Parent, Child; 16 17 ElementType X = A[p]; /* 取出根结点存放的值 */ 18 for( Parent=p; (Parent*2+1) < N; Parent=Child ) { 19 Child = Parent * 2 + 1; 20 if( (Child != N-1) && (A[Child] < A[Child+1]) ) 21 Child++; /* Child指向左右子结点的较大者 */ 22 if( X >= A[Child] ) break; /* 找到了合适位置 */ 23 else /* 下滤X */ 24 A[Parent] = A[Child]; 25 } 26 A[Parent] = X; 27 } 28 29 void HeapSort(ElementType A[], int N) 30 { 31 for(int i = N/2-1; i >= 0; i--)/* 建立最大堆 */ 32 PercDown( A, i, N ); 33 34 for(int i = N-1; i > 0; i--) { 35 /* 删除最大堆顶 */ 36 Swap(&A[0], &A[i] ); 37 PercDown(A, 0, i); 38 } 39 } 40 41 int main() 42 { 43 int a[] = {34,8,64,51,32,21}; 44 HeapSort(a,6); 45 for(int i = 0; i < 6; i++) 46 printf("%d ",a[i]); 47 return 0; 48 }
5.归并排序
归并排序一般不作内排序,在外排序中用
核心:有序子列的归并
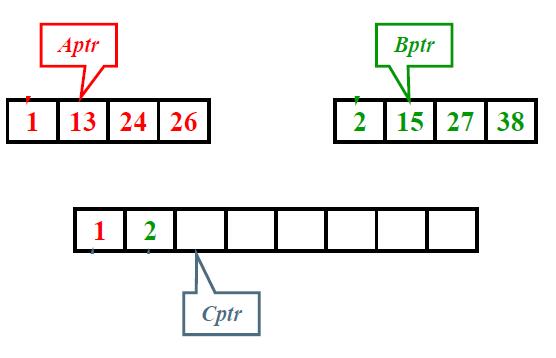

1 /* L = 左边起始位置, R = 右边起始位置, RightEnd = 右边终点位置*/ 2 void Merge( ElementType A[], ElementType TmpA[], int L, int R, int RightEnd ) 3 { /* 将有序的A[L]~A[R-1]和A[R]~A[RightEnd]归并成一个有序序列 */ 4 5 int LeftEnd = R - 1; /* 左边终点位置 */ 6 int temp = L; /* 有序序列的起始位置 */ 7 int NumElements = RightEnd - L + 1; 8 9 while( L <= LeftEnd && R <= RightEnd ) { 10 if ( A[L] <= A[R] ) 11 TmpA[temp++] = A[L++]; /* 将左边元素复制到TmpA */ 12 else 13 TmpA[temp++] = A[R++]; /* 将右边元素复制到TmpA */ 14 } 15 16 while( L <= LeftEnd ) 17 TmpA[temp++] = A[L++]; /* 直接复制左边剩下的 */ 18 while( R <= RightEnd ) 19 TmpA[temp++] = A[R++]; /* 直接复制右边剩下的 */ 20 21 for(int i = 0; i < NumElements; i++, RightEnd -- ) 22 A[RightEnd] = TmpA[RightEnd]; /* 将有序的TmpA[]复制回A[] */ 23 }
递归算法
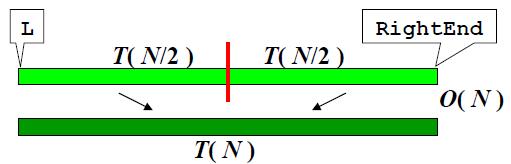
分而治之
T( N ) = O( N logN )
稳定

1 #include <stdio.h> 2 #include <stdlib.h> 3 typedef int ElementType; 4 5 /* 归并排序 - 递归实现 */ 6 7 /* L = 左边起始位置, R = 右边起始位置, RightEnd = 右边终点位置*/ 8 void Merge( ElementType A[], ElementType TmpA[], int L, int R, int RightEnd ) 9 { /* 将有序的A[L]~A[R-1]和A[R]~A[RightEnd]归并成一个有序序列 */ 10 11 int LeftEnd = R - 1; /* 左边终点位置 */ 12 int temp = L; /* 有序序列的起始位置 */ 13 int NumElements = RightEnd - L + 1; 14 15 while( L <= LeftEnd && R <= RightEnd ) { 16 if ( A[L] <= A[R] ) 17 TmpA[temp++] = A[L++]; /* 将左边元素复制到TmpA */ 18 else 19 TmpA[temp++] = A[R++]; /* 将右边元素复制到TmpA */ 20 } 21 22 while( L <= LeftEnd ) 23 TmpA[temp++] = A[L++]; /* 直接复制左边剩下的 */ 24 while( R <= RightEnd ) 25 TmpA[temp++] = A[R++]; /* 直接复制右边剩下的 */ 26 27 for(int i = 0; i < NumElements; i++, RightEnd -- ) 28 A[RightEnd] = TmpA[RightEnd]; /* 将有序的TmpA[]复制回A[] */ 29 } 30 /* 核心递归排序函数 */ 31 void Msort( ElementType A[], ElementType TmpA[], int L, int RightEnd ) 32 { 33 int Center; 34 35 if ( L < RightEnd ) { 36 Center = (L+RightEnd) / 2; 37 Msort( A, TmpA, L, Center ); /* 递归解决左边 */ 38 Msort( A, TmpA, Center+1, RightEnd ); /* 递归解决右边 */ 39 Merge( A, TmpA, L, Center+1, RightEnd ); /* 合并两段有序序列 */ 40 } 41 } 42 /* 归并排序接口函数 */ 43 void MergeSort( ElementType A[], int N ) 44 { 45 ElementType *TmpA; 46 TmpA = (ElementType *)malloc(N*sizeof(ElementType)); 47 48 if ( TmpA != NULL ) { 49 Msort( A, TmpA, 0, N-1 ); 50 free( TmpA ); 51 } 52 else printf( "空间不足" ); 53 } 54 55 int main() 56 { 57 int a[] = {34,8,64,51,32,21}; 58 MergeSort(a,6); 59 for(int i = 0; i < 6; i++) 60 printf("%d ",a[i]); 61 return 0; 62 }
非递归算法
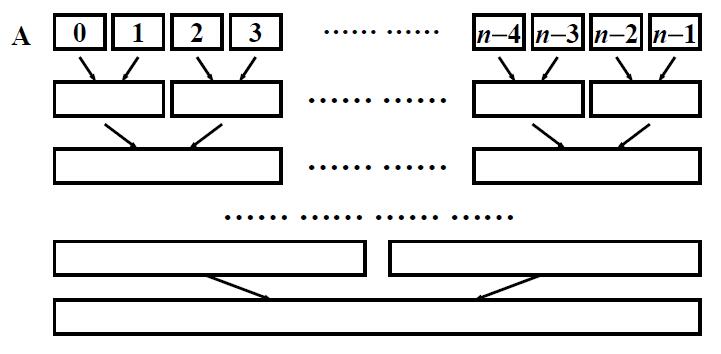
用循环
O(N)
稳定

1 #include <stdio.h> 2 #include <stdlib.h> 3 typedef int ElementType; 4 5 /* 归并排序 - 循环实现 */ 6 7 /* L = 左边起始位置, R = 右边起始位置, RightEnd = 右边终点位置*/ 8 void Merge( ElementType A[], ElementType TmpA[], int L, int R, int RightEnd ) 9 { /* 将有序的A[L]~A[R-1]和A[R]~A[RightEnd]归并成一个有序序列 */ 10 11 int LeftEnd = R - 1; /* 左边终点位置 */ 12 int temp = L; /* 有序序列的起始位置 */ 13 int NumElements = RightEnd - L + 1; 14 15 while( L <= LeftEnd && R <= RightEnd ) { 16 if ( A[L] <= A[R] ) 17 TmpA[temp++] = A[L++]; /* 将左边元素复制到TmpA */ 18 else 19 TmpA[temp++] = A[R++]; /* 将右边元素复制到TmpA */ 20 } 21 22 while( L <= LeftEnd ) 23 TmpA[temp++] = A[L++]; /* 直接复制左边剩下的 */ 24 while( R <= RightEnd ) 25 TmpA[temp++] = A[R++]; /* 直接复制右边剩下的 */ 26 27 for(int i = 0; i < NumElements; i++, RightEnd -- ) 28 A[RightEnd] = TmpA[RightEnd]; /* 将有序的TmpA[]复制回A[] */ 29 } 30 31 /* length = 当前有序子列的长度*/ 32 void Merge_pass( ElementType A[], ElementType TmpA[], int N, int length ) 33 { /* 两两归并相邻有序子列 */ 34 int i, j; 35 36 for ( i = 0; i <= N-2*length; i += 2*length ) 37 Merge( A, TmpA, i, i+length, i+2*length-1 ); 38 if ( i+length < N ) /* 归并最后2个子列*/ 39 Merge( A, TmpA, i, i+length, N-1); 40 else /* 最后只剩1个子列*/ 41 for ( j = i; j < N; j++ ) TmpA[j] = A[j]; 42 } 43 44 void Merge_Sort( ElementType A[], int N ) 45 { 46 int length; 47 ElementType *TmpA; 48 49 length = 1; /* 初始化子序列长度*/ 50 TmpA = (ElementType *)malloc( N * sizeof( ElementType ) ); 51 if ( TmpA != NULL ) { 52 while( length < N ) { 53 Merge_pass( A, TmpA, N, length ); 54 length *= 2; 55 Merge_pass( TmpA, A, N, length ); 56 length *= 2; 57 } 58 free( TmpA ); 59 } 60 else printf( "空间不足" ); 61 } 62 63 int main() 64 { 65 int a[] = {34,8,64,51,32,21}; 66 Merge_Sort(a,6); 67 for(int i = 0; i < 6; i++) 68 printf("%d ",a[i]); 69 return 0; 70 }
