python应用 曲线拟合 01

双指数函数

---

待拟合曲线为 y(x) = be^px + ce^qx

import matplotlib.pyplot as plt

x = ([0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5,
      0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0])
y = ([0.33, 0.26, 0.18, 0.16, 0.12, 0.09, 0.08, 0.07, 0.06, 0.06,
      0.06, 0.07, 0.09, 0.1, 0.15, 0.19, 0.25, 0.36, 0.47, 0.68])

plt.scatter(x, y)
plt.show()

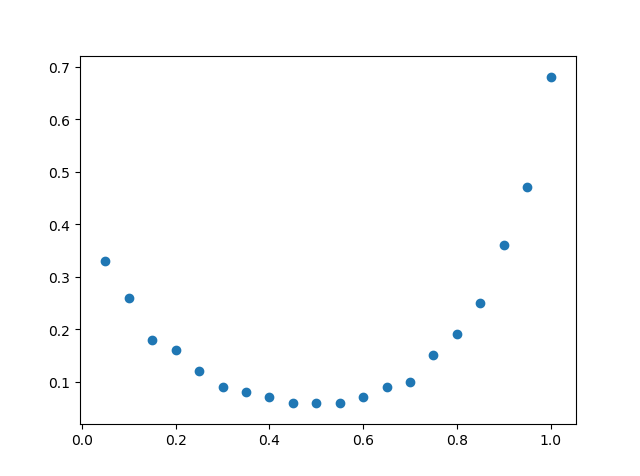
拟合

---

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit


def double_exp(x, b, c, p, q):
    x = np.array(x)
    return b*np.exp(p*x) + c*np.exp(q*x)


x = ([0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5,
      0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0])
y = ([0.33, 0.26, 0.18, 0.16, 0.12, 0.09, 0.08, 0.07, 0.06, 0.06,
      0.06, 0.07, 0.09, 0.1, 0.15, 0.19, 0.25, 0.36, 0.47, 0.68])

popt, pcov = curve_fit(double_exp, x, y, [1, 1, 1, 1])
print(popt)

b = popt[0]
c = popt[1]
p = popt[2]
q = popt[3]

y_fit = double_exp(x, b, c, p, q)

plt.scatter(x, y)
plt.plot(x, y_fit, color='red', linewidth=1.0)

plt.show()

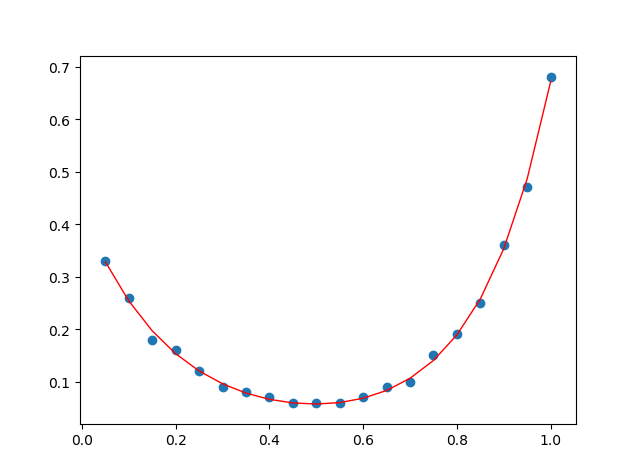
• numpy 库，实现列表转矩阵，得以进行数学运算。
• matplotlib.pyplot 库，绘制图像。
• scipy.optimize 库，curve_fit() 函数，使用非线性最小二乘法拟合曲线。

curve_fit()

• popt，拟合结果，在这里指b, c, p, q 的值。
• povc，该拟合结果对应的协方差。

拟合结果

参数	原函数	拟合结果	误差
b	0.0011	0.0011	0
c	0.4200	0.4242	0.42%
p	6.3998	6.4988	1.55%
q	-5.1551	-5.2164	1.19%

误差可以满意。

经过测试，如果将初始参数设置为原函数参数（保留 4 位小数），拟合得到的结果并未发生变化。

经过测试，拟合使用的三种方法，"trf"，"lm" 和 "dogbox" 对该函数拟合结果影响微乎其微。