
利用的频移性质为:

本习题代码:
%% ------------------------------------------------------------------------
%% Output Info about this m-file
fprintf('
***********************************************************
');
fprintf(' <DSP using MATLAB> Problem 3.9
');
banner();
%% ------------------------------------------------------------------------
% -----------------------------------------------------------
% Rectangle Window sequence, and its DTFT
% -----------------------------------------------------------
%M = 5;
%M = 15;
%M = 25;
M = 100;
n1_start = 0; n1_end = M;
n1 = [n1_start : n1_end - 1];
x1 = ones(1, length(n1));
figure('NumberTitle', 'off', 'Name', sprintf('Problem 3.9 x1(n) Rectangle, M = %d',M));
set(gcf,'Color','white');
stem(n1, x1);
xlabel('n'); ylabel('x1');
title(sprintf('x1(n) sequence, M = %d', M)); grid on;
MM = 500;
k = [-MM:MM]; % [-pi, pi]
%k = [0:M]; % [0, pi]
w = (pi/MM) * k;
[X1] = dtft(x1, n1, w);
magX1 = abs(X1); angX1 = angle(X1); realX1 = real(X1); imagX1 = imag(X1);
figure('NumberTitle', 'off', 'Name', sprintf('Problem 3.9 DTFT of Rm(n), M = %d', M));
set(gcf,'Color','white');
subplot(2,1,1); plot(w/pi, magX1); grid on;
title('Magnitude Part');
xlabel('frequency in pi units'); ylabel('Magnitude');
subplot(2,1,2); plot(w/pi, angX1); grid on;
title('Angle Part');
xlabel('frequency in pi units'); ylabel('Radians');
figure('NumberTitle', 'off', 'Name', sprintf('Problem 3.9 Real and Imag of X1(w), M = %d', M));
set(gcf,'Color','white');
subplot('2,1,1'); plot(w/pi, realX1); grid on;
title('Real Part of X1(w)');
xlabel('frequency in pi units'); ylabel('Real');
subplot('2,1,2'); plot(w/pi, imagX1); grid on;
title('Imaginary Part of X1(w)');
xlabel('frequency in pi units'); ylabel('Imaginary');
%% ----------------------------------------------------------------
%% x(n)=cos(w0*n)Rm(n), and its DTFT
%% ----------------------------------------------------------------
n2 = n1;
w0 = 0.5 * pi;
x2 = cos(w0*n2) .* x1;
%x2 = exp(j*w0*n2) .* x1;
figure('NumberTitle', 'off', 'Name', sprintf('Problem 3.9 x2(n), M = %d', M));
set(gcf,'Color','white');
stem(n2, x2);
xlabel('n2'); ylabel('x2');
title(sprintf('x1(n)*Rm(n) sequence, M = %d', M)); grid on;
MM = 500;
k = [-MM:MM]; % [-pi, pi]
%k = [0:M]; % [0, pi]
w = (pi/MM) * k;
[X2] = dtft(x2, n2, w);
magX2 = abs(X2); angX2 = angle(X2); realX2 = real(X2); imagX2 = imag(X2);
figure('NumberTitle', 'off', 'Name', sprintf('Problem 3.9 DTFT of x2(n), M = %d', M));
set(gcf,'Color','white');
subplot(2,1,1); plot(w/pi, magX2); grid on;
title('Magnitude Part');
xlabel('frequency in pi units'); ylabel('Magnitude');
subplot(2,1,2); plot(w/pi, angX2); grid on;
title('Angle Part');
xlabel('frequency in pi units'); ylabel('Radians');
figure('NumberTitle', 'off', 'Name', sprintf('Problem 3.9 Real and Imag of X2(w), M = %d', M));
set(gcf,'Color','white');
subplot(2,1,1); plot(w/pi, realX2); grid on;
title('Real Part of X2(w)');
xlabel('frequency in pi units'); ylabel('Real');
subplot(2,1,2); plot(w/pi, imagX2); grid on;
title('Imaginary Part of X2(w)');
xlabel('frequency in pi units'); ylabel('Imaginary');
%% --------------------------------------------------------------
%% Direct equation
%% --------------------------------------------------------------
Real_X_direct = 0.5 * cos( (w/pi-w0) * (M-1) / 2) * ( sin( (w/pi-w0)*M/2 ) / sin( (w/pi-w0)/2 ) ) + 0.5 * cos( (w/pi+w0) * (M-1) / 2) * ( sin( (w/pi-(2*pi-w0))*M/2 ) / sin( (w/pi-(2*pi-w0))/2) );
check = sum(abs(realX2)-abs(Real_X_direct))
figure('NumberTitle', 'off', 'Name', 'Problem 3.9 Direct')
set(gcf,'Color',[1,1,1]) % 改变坐标外围背景颜色
plot(w/pi, Real_X_direct); title('Real Part obtained by direct equation');
xlabel('n'); ylabel('Real[x(n)]') ;
grid on;
运行结果:
1、方波窗序列,本题中正弦序列,以及各自DTFT;
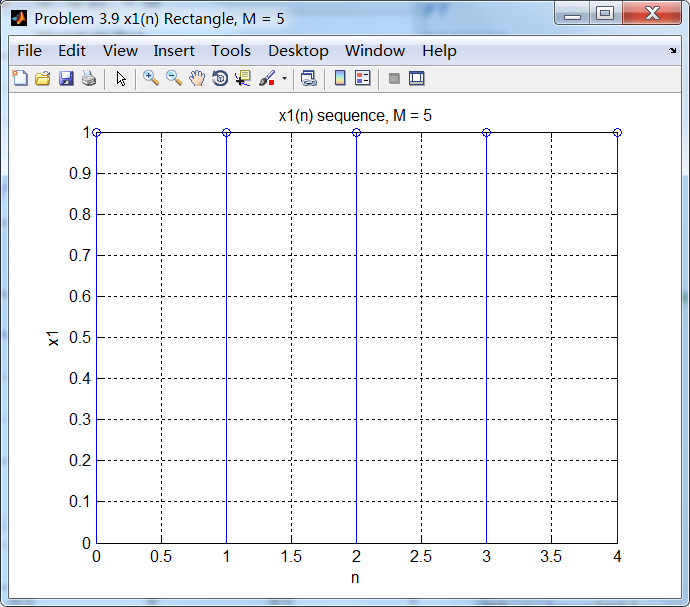
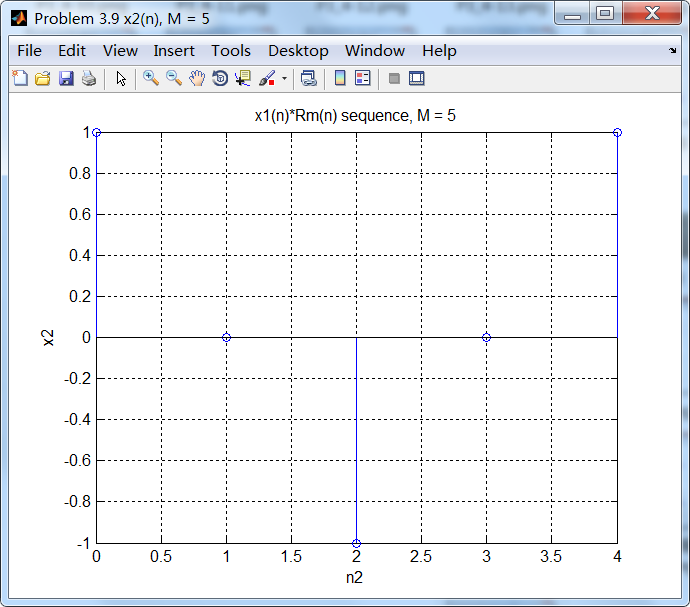
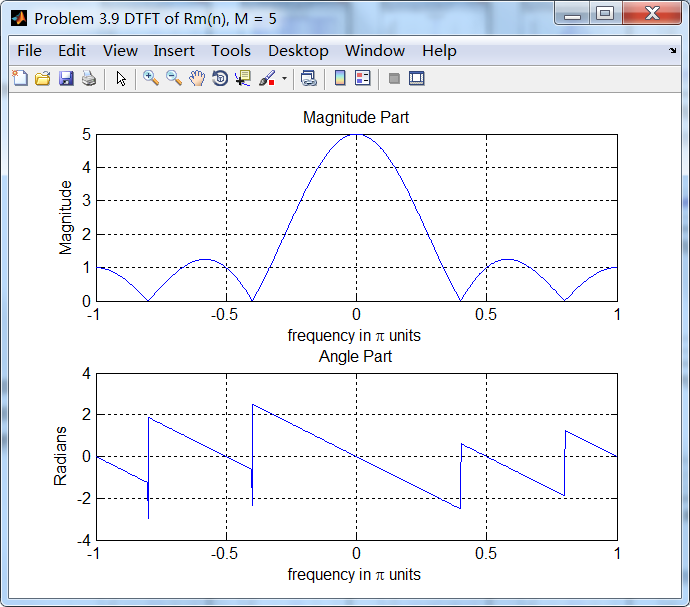
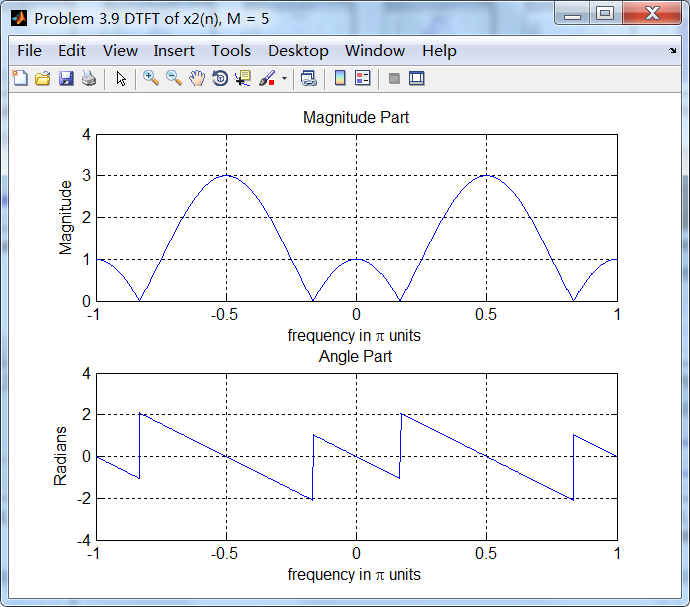
2、谱的实部和虚部;
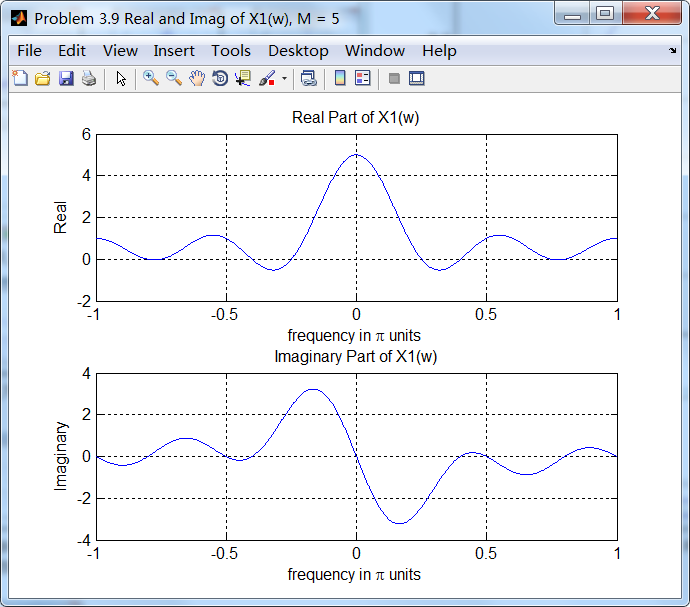
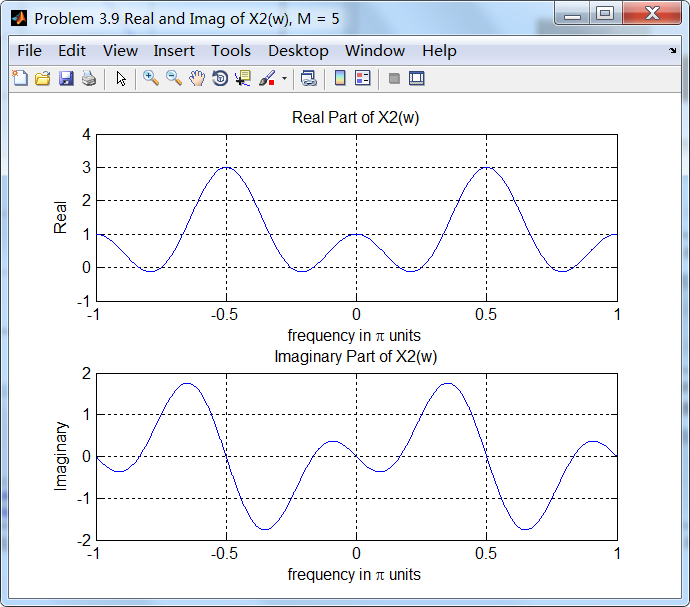
因为ω0=0.5π,根据频移性质,相当于沿着ω轴谱搬移了0.5π(注意到DTFT是以2π为周期的,图中显示的是[-π,π])。