皮克定理

处理何种问题：给定顶点坐标均是整点的任意多边形，

S(面积) = a(内部格点数目) + b(边上格点数目)/2 - 1 。

如图所示：

 

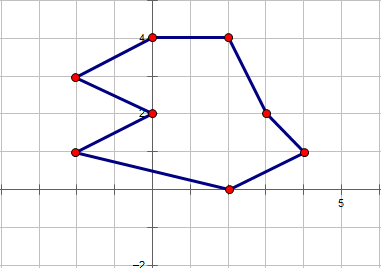
S=14.50

a=11

b=9（最上方的边内有一整数点）

 

性能：时间复杂度为 O（n）。

 

原理：皮克定理我在这里就不贴证明资料了。对于多边形面积的求法用的是叉积求法。在这里重点说一下--b(边上格点数目)的求法：对于两个顶点构成的线段所覆盖到的整数顶点的个数=GCD（dx，dy）+1。（dx为横坐标之差，dy为纵坐标之差）

 

实现步骤：叉乘求面积+上述方法求b

 

备注：因为求的是一个封闭图形的b数目，所以可以不用+1了；必须逆时针输入顶点。

 

输入样例解释：

8  //顶点个数

2 0 //顶点坐标

4 1

3 2

2 4

0 4

-2 3

0 2

-2 1

 

输出样例解释：

S=14.50  //多边形面积

a=11  //多边形内部格点数目

b=9   //多边形边上格点数目

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<string.h>
#include<cmath>
#include<string>
using namespace std;
struct Point
{
    double x,y;
};
Point arr[10010];

int GCD(int a,int b)//有些c++的环境是不支持__gcd();
{
    int temp;
    while(a!=0)
    {
        temp=a;
        a=b%a;
        b=temp;
    }
    return b;
}
int main()
{
    int n,x,y,sum_a,sum_b;
    double area=0,x1,y1,x2,y2;
    while(~scanf("%d",&n))
    {
        sum_a=sum_b=area=0;
        for(int i=0;i<n;++i)
            scanf("%lf%lf",&arr[i].x,&arr[i].y);

        for(int i=1;i<n;++i)
        {
            x=abs(arr[i].x-arr[i-1].x);
            y=abs(arr[i].y-arr[i-1].y);
            sum_b+=GCD(x,y);         //因为求的是一个封闭图形的b数目，所以可以不用+1了
        }
        x=abs(arr[0].x-arr[n-1].x);
        y=abs(arr[0].y-arr[n-1].y);
        sum_b+=GCD(x,y);



        for(int i=0;i<n-1;++i)
        {
            x1=arr[i].x-arr[0].x;
            y1=arr[i].y-arr[0].y;

            x2=arr[i+1].x-arr[0].x;
            y2=arr[i+1].y-arr[0].y;

            area+=(x1*y2-x2*y1)/2;
        }

        sum_a=area-sum_b*1.0/2+1;
        printf("S=%.2lf
",area);
        printf("a=%d
",sum_a);
        printf("b=%d
",sum_b);
    }
    return 0;
}