BMY、KMP、BM、BMHS算法性能比较

　　前些日子研究了一下字符串匹配算法，突发奇想自己设计了一种新的字符串匹配算法，因为是基于BM的思想，所以暂且叫他BMY算法吧。传统的BM算法是基于坏字符规则和好后缀规则，从后向前的匹配字符串，每次发现失配时，会比较坏字符表和好后缀表，哪个对应的跳跃值大就用哪个跳跃值，这样的跳跃幅度比KMP算法要大很多。而我设计的BMY算法在失配后（失配字符称为尾1），会再比较一下失配字符前面那个字符（称为尾2）：如果尾1和尾2都不在模式串中，直接跳跃模式串长度+2；如果尾1在模式串尾，则跳跃1；如果尾1和尾2的组合在模式串中，则跳跃模式串长度-尾1尾2在模式串中的位置；如果尾2在模式串头，则跳跃模式串长度+1；其他情况一律跳跃模式串长度+2。流程框图如下：

　　　　　　

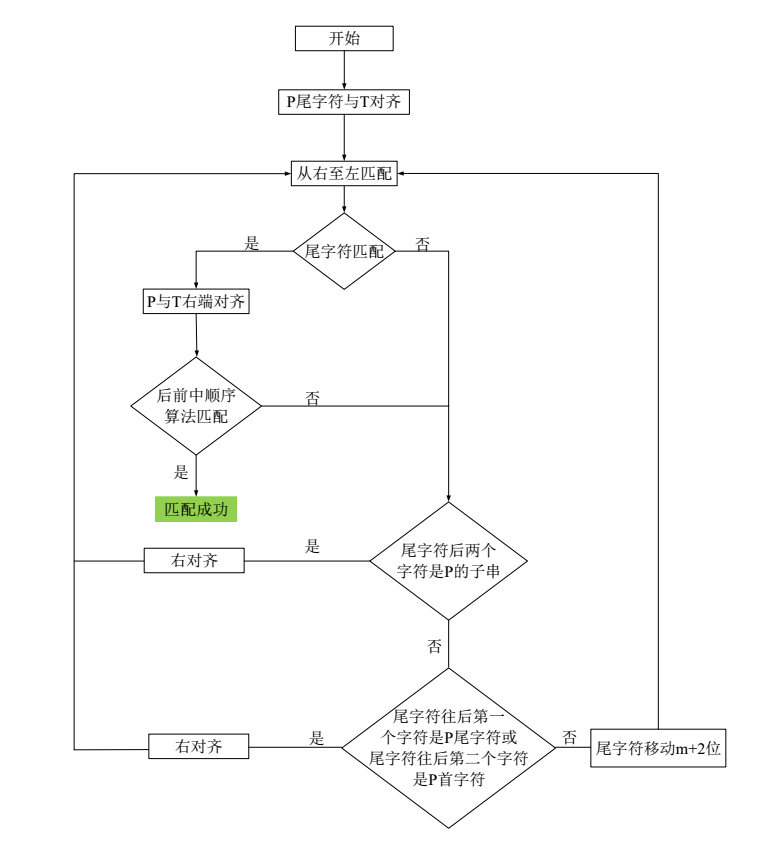
　　BMY算法设计维护了两张哈希表，其中哈希表m1用于验证匹配到的字符是否在模式串，哈希表m2存储【尾1+尾2】的双字符在模式串中的位置，具体的代码如下：

void BMY(string &pstr, const size_t &plen, string &sstr, const size_t &slen, int (&m1)[ALPHABET_SIZE], int (&m2)[ZuHe_SIZE], vector<int> &res)
{
    int i,j;  //i:模式串游标   j:文本串游标 
    i = j = plen-1; 
    int cnt = -1;
    while(j < slen)
    {
        num_bmy++;
        //模式串和文本串从后向前匹配 
        while( (i!=0) && pstr[i] == sstr[j])
        {
            --i;
            --j;
            bidui_bmy++;
        }
        bidui_bmy++;
        //发现一个匹配的模式串 
        if(i==0 && pstr[i] == sstr[j])
        {
            res.push_back(j);
            match_bmy++;
        }    
        //匹配成功及出现失配的情况 
        j += (plen-i-1);
        if(m1[sstr[j+1]] == 0 && m1[sstr[j+2]] == 0)            //尾1和尾2都不在模式串中
            j += (plen + 2);
        else if(sstr[j+1] == pstr[plen-1])                      //尾1在模式串尾
            j += 1;
        else if( (cnt = m2[sstr[j+1]*256+sstr[j+2]]) != -1)     //尾1和尾2的组合在模式串中 
            j += (plen - cnt); 
        else if(sstr[j+2] == pstr[0])                           //尾2在模式串头 
            j += (plen + 1);
        else
            j += (plen + 2);
        cnt = -1;
        i = plen - 1;
    }
}

　　最后，比较KMP、BM、BMHS、BMY四种算法的匹配时间、匹配次数、比对次数，得到的结果如下：

　　　　　　

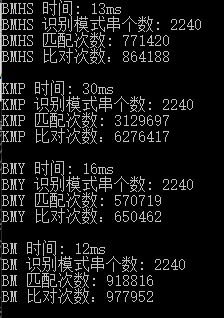
　　 从结果可以看出，自己设计的BMY算法和BM、BMHS相比时间性能上略差，但是已经比KMP强很多了。此外，BMY的匹配次数和比对次数明显少于其他算法，但在运行时间上却没有对应的优势，我猜想是BMY在选择跳跃幅度上做了太多选择比较耗费了时间。

　　下面贴出全部测试代码：

#include <iostream>
#include <cstring>
#include <sstream>
#include <vector>
#include <algorithm>
#include <unordered_map>
#include <map>
#include <ctime>
#include <iterator>
#include <fstream>
using namespace std;

#define ALPHABET_SIZE 32767
#define ZuHe_SIZE 32767

int match_kmp = 0;
int match_bmy = 0;
int match_bm = 0;
int match_bmhs = 0;

int num_kmp = 0;
int num_bmy = 0;
int num_bm = 0;
int num_bmhs = 0;

int bidui_kmp = 0;
int bidui_bm = 0;
int bidui_bmy = 0;
int bidui_bmhs = 0;

void InitBMHS(int *alphabet, string &des, size_t plen)
{
    for (int i=0; i<ALPHABET_SIZE; i++)
        alphabet[i] = plen;
    for (int i=0; i<plen; i++)
        alphabet[des[i]] = plen - i - 1;
}

void sunday(string &src, size_t len_s, string &des, size_t len_d, int *alphabet, vector<int> &res)
{
    int i, pos = 0;

    for (pos = 1; pos <= len_s - len_d + 1;)
    {
        num_bmhs++;
        for (i=pos+len_d-2; i>=pos-1 ; i--)
        {
            if (src[i] == des[i-pos+1])
            { 
                bidui_bmhs++;
            } 
            else if (src[i] != des[i-pos+1])
            {
                bidui_bmhs++;
                break;
            }
        }
        if ((i-pos+2+len_d) == len_d)
        {
            match_bmhs++;
            res.push_back(pos-1);
            pos += len_d;
        }
        else
        {
            pos += alphabet[src[pos+len_d-1]] + 1;
        }
    }
}

void initP(string &pstr, int (&m1)[ALPHABET_SIZE], int (&m2)[ZuHe_SIZE])
{
    int len = pstr.size();
    for(int i=0; i<len; ++i)
    {
        m1[pstr[i]] = 1;
    }
    for(int i=0; i<len-1; ++i)
    {
        m2[pstr[i]*256+pstr[i+1]] = i;
    }
}

void BMY(string &pstr, const size_t &plen, string &sstr, const size_t &slen, int (&m1)[ALPHABET_SIZE], int (&m2)[ZuHe_SIZE], vector<int> &res)
{
    int i,j;  //i:模式串游标   j:文本串游标 
    i = j = plen-1; 
    int cnt = -1;
    while(j < slen)
    {
        num_bmy++;
        //模式串和文本串从后向前匹配 
        while( (i!=0) && pstr[i] == sstr[j])
        {
            --i;
            --j;
            bidui_bmy++;
        }
        bidui_bmy++;
        //发现一个匹配的模式串 
        if(i==0 && pstr[i] == sstr[j])
        {
            res.push_back(j);
            match_bmy++;
        }    //匹配成功及出现失配的情况 
        j += (plen-i-1);
        if(m1[sstr[j+1]] == 0 && m1[sstr[j+2]] == 0)          //尾1和尾2都不在模式串中
            j += (plen + 2);
        else if(sstr[j+1] == pstr[plen-1])                    //尾1在模式串尾
            j += 1;
        else if( (cnt = m2[sstr[j+1]*256+sstr[j+2]]) != -1)   //尾1和尾2的组合在模式串中 
            j += (plen - cnt); 
        else if(sstr[j+2] == pstr[0])                         //尾2在模式串头 
            j += (plen + 1);
        else
            j += (plen + 2);
        cnt = -1;
        i = plen - 1;
    }
}

void GetNext(string p, int (&next)[ALPHABET_SIZE])  
{  
     int pLen = p.size();  
     next[0] = -1;  
     int k = -1;  
     int j = 0;  
     while (j < pLen-1 )  
     {  
         if(k == -1 || p[j] == p[k]) //p[k]表示前缀，p[j]表示后缀   
         {  
             ++k;  
             ++j;  
             next[j] = k;  // k == next[j-1] + 1
         }  
         else   
         {  
             k = next[k];  // next[k] == next[next[j]](递归的思想）
         }  
     }  
}  

void KMP_Search(string &s, size_t slen, string &p, size_t plen, int (&next)[ALPHABET_SIZE], vector<int> &res)  
{  
     int i = 0;  
    int j = 0;  
    while (j < slen)  // i:模式串游标  j:文本串游标 
    {  
        num_kmp++;
        //模式串和文本串从前向后匹配      
        while(i == -1 || s[j] == p[i])  
          {  
              i++;  
             j++;
             bidui_kmp++;
            if(i == plen) 
                break; 
          }
          bidui_kmp++;
        //找到匹配的模式串  
          if(i == plen)
          {
               res.push_back(j-i);
            j += 1;
            i = 0;         
            match_kmp++;
        }
        //出现失配的情况 
         else  
         {  
                 //如果i != -1，且当前字符匹配失败（即S[i] != P[j]），则令j不变，i = next[j],使模式串右移    
             i = next[i];  
         }  
     }  
} 

void BuildBadC(string &pattern, size_t pattern_length, unsigned int *badc, size_t alphabet_size)  
{  
    unsigned int i;  
    for(i = 0; i < alphabet_size; ++i)  
    {  
        badc[i] = pattern_length;  
    }  
  
    for(i = 0; i < pattern_length; ++i)  
    {  
        badc[pattern[i] ] = pattern_length - 1 - i;  
    }  
}  

void BuildGoodS(const char *pattern, size_t pattern_length, unsigned int* goods)  
{  
    unsigned int i, j, c;  
    for(i = 0; i < pattern_length - 1; ++i)  
    {  
        goods[i] = pattern_length;  
    }  
  
    //初始化pattern最末元素的好后缀值  
    goods[pattern_length - 1] = 1;  
  
    //此循环找出pattern中各元素的pre值，这里goods数组先当作pre数组使用  
    for(i = pattern_length -1, c = 0; i != 0; --i)  
    {  
        for(j = 0; j < i; ++j)  
        {  
            if(memcmp(pattern + i, pattern + j, (pattern_length - i) * sizeof(char)) == 0)  
            {  
                if(j == 0)  
                {  
                    c = pattern_length - i;  
                }  
                else  
                {  
                    if(pattern[i - 1] != pattern[j - 1])  
                    {  
                        goods[i - 1] = j - 1;  
                    }  
                }  
            }  
        }  
    }  
    
    //根据pattern中个元素的pre值，计算goods值  
    for(i = 0; i < pattern_length - 1; ++i)  
    {  
        if(goods[i] != pattern_length)  
        {  
            goods[i] = pattern_length - 1 - goods[i];  
        }  
        else  
        {  
            goods[i] = pattern_length - 1 - i + goods[i];  
  
            if(c != 0 && pattern_length - 1 - i >= c)  
            {  
                goods[i] -= c;  
            }  
        }  
    }  
}  

void BM(string &pattern, size_t pattern_length, string &text, size_t text_length, unsigned int *badc, unsigned int *goods, vector<int> &res)  
{  
    unsigned int i, j;  
    i = j = pattern_length - 1;  
    while(j < text_length)  
    {  
        num_bm++;
        //发现目标传与模式传从后向前第1个不匹配的位置  
        while((i != 0) && (pattern[i] == text[j]))  
        {  
            --i;  
            --j;  
            bidui_bm++;
        }  
          bidui_bm++;
        //找到一个匹配的情况  
        if(i == 0 && pattern[i] == text[j])  
        {  
            res.push_back(j);  
            j += goods[0];  
            match_bm++;
        }  
        else  
        {  
            //坏字符表用字典构建比较合适  
            j += goods[i] > badc[text[j]] ? goods[i] : badc[text[j]];  
        }  
  
        i = pattern_length - 1;  
    }  
}  

int main()
{
    string pstr = "want";
    ifstream fin("2.txt");
    string sstr( (istreambuf_iterator<char>(fin)), istreambuf_iterator<char>() );
    for(int i=0; i<5; i++)
        sstr.insert(sstr.end(),sstr.begin(),sstr.end());
    const char* pstr_ = pstr.data();

    const size_t plen = pstr.size();
    const size_t slen = sstr.size();
    
    /*BMHS*/
    int alphabet[ALPHABET_SIZE] = { 0 };
    InitBMHS(alphabet, pstr, plen);
    vector<int> res4;
    clock_t start4 = clock();
    sunday(sstr, slen, pstr, plen, alphabet, res4); 
    cout<<"BMHS 时间: "<<(double)(clock()-start4)/CLOCKS_PER_SEC*1000<<"ms"<<endl;
    cout<<"BMHS 识别模式串个数: "<<match_bmhs<<endl;
    cout<<"BMHS 匹配次数: "<<num_bmhs<<endl;
    cout<<"BMHS 比对次数："<<bidui_bmhs<<endl<<endl;
//    for(auto it : res4)
//        cout<<it<<endl;

    /*KMP*/
    int next[ALPHABET_SIZE];
    for(int i=0; i<ALPHABET_SIZE; i++)
        next[i] = -1;
    GetNext(pstr, next);
    vector<int> res2;
    clock_t start2 = clock();
    KMP_Search(sstr, slen, pstr, plen, next, res2);    
    cout<<"KMP 时间: "<< (double)(clock()-start2)/CLOCKS_PER_SEC*1000<<"ms"<<endl; 
    cout<<"KMP 识别模式串个数: "<<match_kmp<<endl;
    cout<<"KMP 匹配次数: "<<num_kmp<<endl;
    cout<<"KMP 比对次数："<<bidui_kmp<<endl<<endl;
//    for(auto it : res2)
//        cout<<it<<endl;

    /*BMY*/
    int m1[ALPHABET_SIZE] = {0};
    int m2[ZuHe_SIZE];
    for(int i=0; i<ZuHe_SIZE; i++)
        m2[i] = -1;
    initP(pstr, m1, m2);
    vector<int> res1;
    clock_t start = clock();
    BMY(pstr, plen, sstr, slen, m1, m2, res1);
    cout<<"BMY 时间: "<< (double)(clock()-start)/CLOCKS_PER_SEC*1000<<"ms"<<endl; 
    cout<<"BMY 识别模式串个数: "<<match_bmy<<endl;
    cout<<"BMY 匹配次数: "<<num_bmy<<endl;
    cout<<"BMY 比对次数："<<bidui_bmy<<endl<<endl;
//    for(auto it : res1)
//        cout<<it<<endl;

    /*BM*/
    unsigned int badc[256];  
    unsigned int goods[plen];
    BuildBadC(pstr, plen, badc, 256);  
    BuildGoodS(pstr_, plen, goods); 
    vector<int> res3;
    clock_t start3 = clock();
    BM(pstr, plen, sstr, slen, badc, goods, res3);
    cout<<"BM 时间: "<< (double)(clock()-start3)/CLOCKS_PER_SEC*1000<<"ms"<<endl; 
    cout<<"BM 识别模式串个数: "<<match_bm<<endl;
    cout<<"BM 匹配次数: "<<num_bm<<endl;
       cout<<"BM 比对次数："<<bidui_bm<<endl<<endl;
//    for(auto it : res3)
//        cout<<it<<endl;
    
    return 0;
}