晶振相关（一）

参考文献

【1】晶振电路探究性实验设计 实验技术与管理 陈世海等

【2】ST inc. Application note AN2867

【3】高频电子线路（第二版） 高等教育出版社 曾兴雯等

1.啥是晶体振荡器与晶体振荡器的主要特性

石英晶体具有正反压电效应，将其按照一定的方向切割成石英晶片，两边敷上银电极并且焊上引脚，用金属或者玻璃封装之后即构成了晶振。通常晶振的机械系统（组成方式）类比于电系统，也就是把石英晶片的质量类比于电感，弹性类比于电容，机械摩擦类比于电阻。（见【1】）如下图

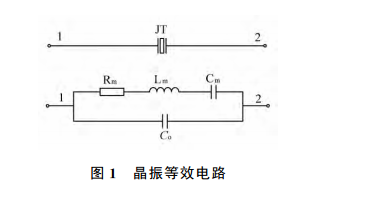
(L_m)动态电感，取决于晶片厚度；

(C_m)动态电容，取决于晶片尺寸和电极面积；

(R_m)动态电阻，取决于机械损耗；

晶片之外的封装啊，焊盘引脚啊这些会构成一个静电容(C_0)。

从该模型的假设出发

(Z(omega) = (R_m + j omega L_m + frac{1}{j omega C_m}) // (frac{1}{jomega C_0}))

就可以得出这样的一个结果。但是直接计算的话结果会显得过于复杂，所以需要进行进行一些简化。参看这个公式：

[Z(omega) = frac{(R_m + j omega L_m + frac{1}{j omega C_m})(frac{1}{jomega C_0})}{ (R_m + j omega L_m + frac{1}{j omega C_m}) + (frac{1}{jomega C_0})} ]

一般来说，适应晶振的Q值很高（参考【3】page156 石英晶振Q值应该在(10^4) ~ (10^6)之间），甚至在有些文献【2】当中，(R_m) 在整个的讨论都被当成是可以忽略的量，所以可以把分子上面的(R_m)抹去，那么我们只要让分母虚部的结果等于0即可。
于是乎得到：

[Z(omega) = frac{j}{omega} imes frac{omega^2 L_m C_m -1}{(C_0 +C_m)- omega^2 L_m C_m C_0} ]

令分子分母等于零，我们可以得到两个特殊的谐振点。谐振点1满足(f_s = frac{1}{2 pi sqrt{L_m C_m}})跟一般的串联谐振定义比较相似，谐振点2满足(f_a = f_s sqrt{1+frac{C_m}{C_0}})，频点在此处时对外阻抗等于无穷大，而且此时左右处频点符号相异，这时比较接近并联谐振的定义，在文献（2）当中称之为反谐振点（anti-resonant）

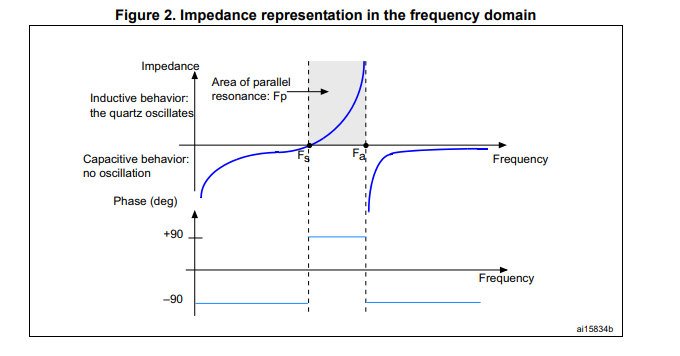
但是实际使用的时候，一般并不是晶振自身形成谐振的，这样的话频点固定，难以调谐，所以一般加上负载电容(C_L)。这样的话，并联谐振的频点可以表达成(f_p = f_s sqrt{1+C_m /2(C_0 + C_L)})，使用泰勒公式可以把结果简化为

[f_p = f_s (1+ frac{C_m}{2(C_0 + C_L)}) ]