同志,你的Manacher掉了
引入(建议跳过):
1.当你求最长回文子串的时候是否陷入过绝望。
2.当你求回文的时候是否T飞
3.当你想不出来怎么优化复杂度的时候
————Manacher来了。
最长回文子串的求法:
众所周知,回文串的定义是:正过来和反过来是一样的
比如 ABA 是回文串 ,ABC就不是,ABBCBBA是,ABB不是。
那么我们就有了暴力求法:
1.O(n3)
即暴力枚举一段子串,看他正过来反过来一不一样
1 #include<bits/stdc++.h> 2 using namespace std; 3 int ans; 4 string str; 5 int main() 6 { 7 cin>>str; 8 int long_=str.size(); 9 for(int i=1;i<long_;++i) 10 for(int j=i;j<long_;++j) 11 { 12 string tmp=str.substr(i-1,j-i+1),tmp2=""; 13 for(int p=j;p>=i;--p) 14 tmp2=tmp2+str[p]; 15 if(tmp2==tmp) ans=max(ans,j-i+1); 16 } 17 printf("%d",ans); 18 return 0; 19 }
2.O(n2)
我们也可以确定一个回文中心,通过这个中心往外扩展。
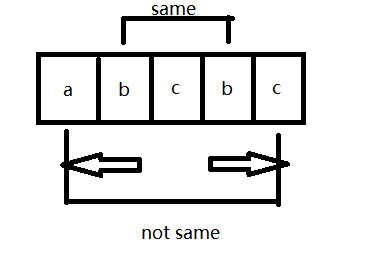
如上图,以c为中心的最长回文子串为bcb,就是以c为中心,往两边扩展
ABBA这个回文串是以BB为中心的,ABA则是以B为中心的。
你会发现奇数长度的回文串中心是奇数的,偶数长的回文串中心是偶数的,这不好搞。
于是有了一个技巧。往期间插入'#'号隔开,这样回文串必定是奇数的。
举个例子:abbab这个串。

以bb为中心的串在这里面是以‘#’为中心的串。
那么最长串应该是#a#b#b#a#
是以第6位的#作为中心,半径为5的一个串。
再举个例子,#b#a#b#是以a为中心,半径为4的一个串。
需要注意的是,这个串实际最右边的位置是:回文中心+半径-1
那么回文串实际长度(不算#的长度)=半径-1.
这个公式是毋庸置疑的。
你可能会问@是干嘛用的,@是用来强制判断回文串到头了(没有一个串中会有2个@所以扫到@就肯定不能构成回文串),不然可能会越界。
那么代码可以这样写
1 #include<bits/stdc++.h> 2 #define maxn 12000005 3 using namespace std; 4 char a[maxn<<1]; 5 int num,ans; 6 void in_() 7 { 8 char ch=getchar(); 9 a[0]='@'; 10 while(ch>'z'||ch<'a') ch=getchar(); 11 while(ch>='a'&&ch<='z'){a[++num]='#',a[++num]=ch,ch=getchar();} 12 a[++num]='#'; 13 return; 14 } 15 int main() 16 { 17 in_(); 18 for(int i=1;i<=num;++i) 19 { 20 int k=1; 21 while(a[i-k]==a[i+k]) ++k; 22 ans=max(ans,k-1); 23 } 24 printf("%d",ans); 25 return 0; 26 }
3.O(n)
这种O(n)操作就是manacher算法。
这种算法是基于O(n^2)操作上的,可以当作是一种超级优化。
我们知道,当O(n^2)的算法运行时,会有很多重复,就是很多回文串会交织在一起。

如上图,橙色线条是回文串abba,红色线条是回文串bab
期间红色和橙色有重叠部分
我们每次记录一个最大的r值,同时记录mid和l,分别是这个r的回文串的回文中心和最左边

我们可以肯定的是,l到r中间是一个回文串。
那么我们可以想,当bab的回文中心a在l和r中间,那么在mid*2-now的位置上也会有一个a
这个一定要想清楚,因为是回文串,所以从l开始到mid和r开始到mid是互相对应的。
那么a在mid到r中存在,a一定在l到mid中存在。
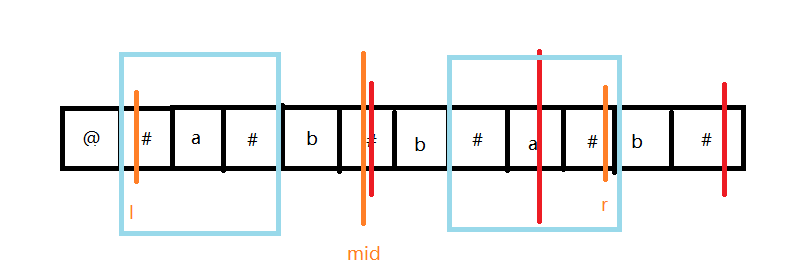
如图所示,我们现在可以肯定的是,a的回文串一定>=左边的a在l到r中间的回文串部分。
这个也很绕,右边a的回文串一定包括左边的蓝色方框的回文串,因为l到r是一个回文串
但是我们也想,如果左边的蓝色方框的左边超过l,即超出l到r的范围,如下图
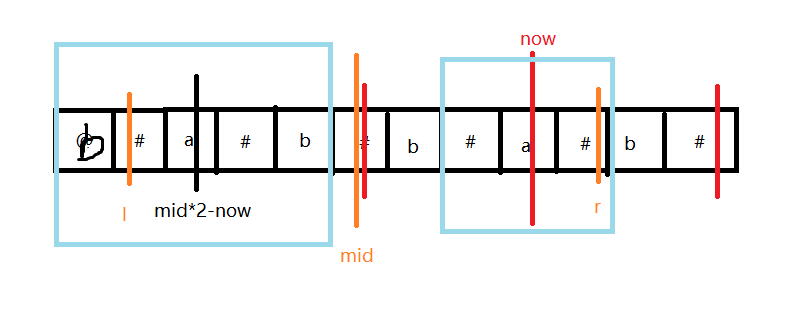
那么右边的a目前可以确定的回文半径是r-now
所以
半径a=min(半径mid*2-now,r-now+1);
于是代码就出来了
1 #include<bits/stdc++.h> 2 #define maxn 12000005 3 using namespace std; 4 char a[maxn<<1]; 5 int num,r,mid,ans,b[maxn<<1]; 6 void in_() 7 { 8 char ch=getchar();a[0]='@'; 9 while(ch>'z'||ch<'a') ch=getchar(); 10 while(ch>='a'&&ch<='z'){a[++num]='#',a[++num]=ch,ch=getchar();} 11 a[++num]='#'; 12 return; 13 } 14 int main() 15 { 16 in_(); 17 for(int i=1;i<=num;++i) 18 { 19 if(i<=r) b[i]=min(b[(mid<<1)-i],r-i+1);//i<=r是L到R的范围内 20 while(a[i-b[i]]==a[i+b[i]]) ++b[i]; 21 if(i+b[i]>=r) r=i+b[i]-1,mid=i; 22 ans=max(ans,b[i]); 23 } 24 printf("%d",ans-1);//真实长度=半径-1 25 return 0; 26 }
QAQ我太蒟蒻了,manacher都讲不清楚