一、正整数的十进制转换二进制:
要点:除二取余,倒序排列,高位补0
例如把52换算成二进制数,计算结果如图:
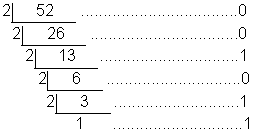
52除以2得到的余数依次为:0、0、1、0、1、1,倒序排列,所以52对应的二进制数就是110100。
由于计算机内部表示数的字节单位都是定长的,以2的幂次展开,或者8位,或者16位,或者32位。
于是,一个二进制数用计算机表示时,位数不足2的幂次时,高位上要补足若干个0。本文都以8位为例。那么:
(52)10=(00110100)2
二、负整数转换为二进制
要点:取反加一
解释:将该负整数对应的正整数先转换成二进制,然后对其“取补”,再对取补后的结果加1即可
例如要把-52换算成二进制:
1.先取得52的二进制:00110100
2.对所得到的二进制数取反:11001011
3.将取反后的数值加一即可:11001100
即:(-52)10=(11001100)2
三、二进制转换为十进制:
整数二进制用数值乘以2的幂次依次相加,小数二进制用数值乘以2的负幂次然后依次相加!
比如将二进制110转换为十进制:
首先补齐位数,00000110,首位为0,则为正整数,那么将二进制中的三位数分别于下边对应的值相乘后相加得到的值为换算为十进制的结果
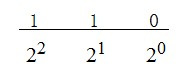

如果二进制数补足位数之后首位为1,那么其对应的整数为负,那么需要先取反然后再换算
比如11111001,首位为1,那么需要先对其取反,即:-00000110
00000110,对应的十进制为6,因此11111001对应的十进制即为-6
换算公式可表示为:
11111001=-00000110
=-6