计数器法
计数器法是限流算法里最简单也是最容易实现的一种算法。比如我们规定,对于A接口来说,我们1分钟的访问次数不能超过100个。那么我们可以这么做:在一开 始的时候,我们可以设置一个计数器counter,每当一个请求过来
的时候,counter就加1,如果counter的值大于100并且该请求与第一个 请求的间隔时间还在1分钟之内,那么说明请求数过多;如果该请求与第一个请求的间隔时间大于1分钟,且counter的值还在限流范围内,那么就重置
counter,具体算法的示意图如下:
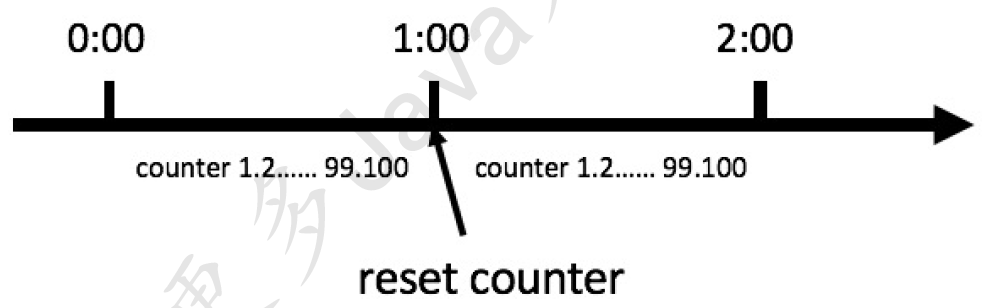
这个算法虽然简单,但是有一个十分致命的问题,那就是临界问题,我们看下图:

从上图中我们可以看到,假设有一个恶意用户,他在0:59时,瞬间发送了100个请求,并且1:00又瞬间发送了100个请求,那么其实这个用户在 1秒里面,瞬间发送了200个请求。我们刚才规定的是1分钟最多100个请求,也就是每秒钟最多1.7个请求,用户通过在时间窗口的重置节点处突发请求,
可以瞬间超过我们的速率限制。用户有可能通过算法的这个漏洞,瞬间压垮我们的应用。聪明的朋友可能已经看出来了,刚才的问题其实是因为我们统计的精度太低。那么如何很好地处理这个问题呢?或者说,如何将临界问题的影响降低呢?我们可以看下面的滑动窗口算法。
滑动窗口
滑动窗口,又称rolling window。为了解决这个问题,我们引入了滑动窗口算法。如果学过TCP网络协议的话,那么一定对滑动窗口这个名词不会陌生。下面这张图,很好地解释了滑动窗口算法: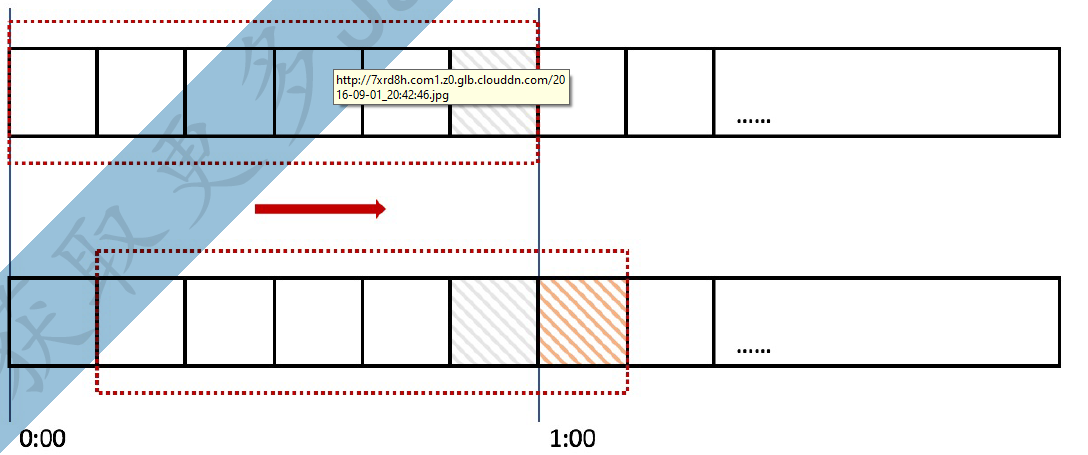
在上图中,整个红色的矩形框表示一个时间窗口,在我们的例子中,一个时间窗口就是一分钟。然后我们将时间窗口进行划分,比如图中,我们就将滑动窗口 划成了6格,所以每格代表的是10秒钟。每过10秒钟,我们的时间窗口
就会往右滑动一格。每一个格子都有自己独立的计数器counter,比如当一个请求 在0:35秒的时候到达,那么0:30~0:39对应的counter就会加1。那么滑动窗口怎么解决刚才的临界问题的呢?我们可以看上图,0:59到达的100个请求
会落在灰色的格子中,而1:00到达的请求会落在橘黄色的格 子中。当时间到达1:00时,我们的窗口会往右移动一格,那么此时时间窗口内的总请求数量一共是200个,超过了限定的100个,所以此时能够检测出来触 发了限流。我再
来回顾一下刚才的计数器算法,我们可以发现,计数器算法其实就是滑动窗口算法。只是它没有对时间窗口做进一步地划分,所以只有1格。由此可见,当滑动窗口的格子划分的越多,那么滑动窗口的滚动就越平滑,限流的统计就会越精确。
漏桶算法
漏桶算法,又称leaky bucket。为了理解漏桶算法,我们看一下维基百科上的对于该算法的示意图:
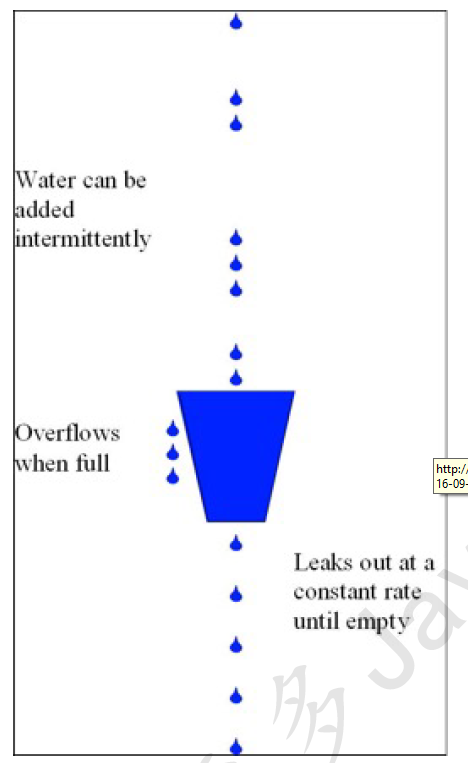
从图中我们可以看到,整个算法其实十分简单。首先,我们有一个固定容量的桶,有水流进来,也有水流出去。对于流进来的水来说,我们无法预计一共有多 少水会流进来,也无法预计水流的速度。但是对于流出去的水来说,这个桶可以固定水流出的速率。而且,当桶满了之后,多余的水将会溢出
我们将算法中的水换成实际应用中的请求,我们可以看到漏桶算法天生就限制了请求的速度。当使用了漏桶算法,我们可以保证接口会以一个常速速率来处理请求。所以漏桶算法天生不会出现临界问题。
令牌桶算法
令牌桶算法,又称token bucket。为了理解该算法,我们再来看一下维基百科上对该算法的示意图: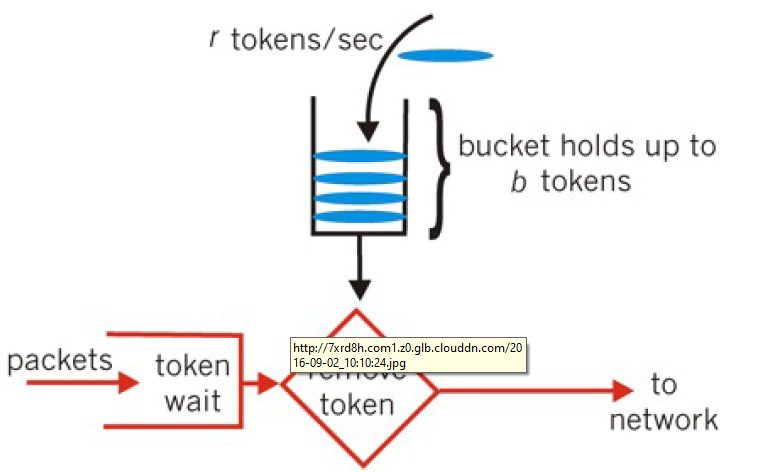
从图中我们可以看到,令牌桶算法比漏桶算法稍显复杂。首先,我们有一个固定容量的桶,桶里存放着令牌(token)。桶一开始是空的,token以 一个固定的速率r往桶里填充,直到达到桶的容量,多余的令牌将会被丢
弃。每当一个请求过来时,就会尝试从桶里移除一个令牌,如果没有令牌的话,请求无法通 过。
令牌桶
令牌桶算法是网络流量整形(Traffic Shaping)和速率限制(Rate Limiting)中最常使用的一种算法。典型情况下,令牌桶算法用来控制发送到网络上的数据的数目,并允许突发数据的发送(百科)。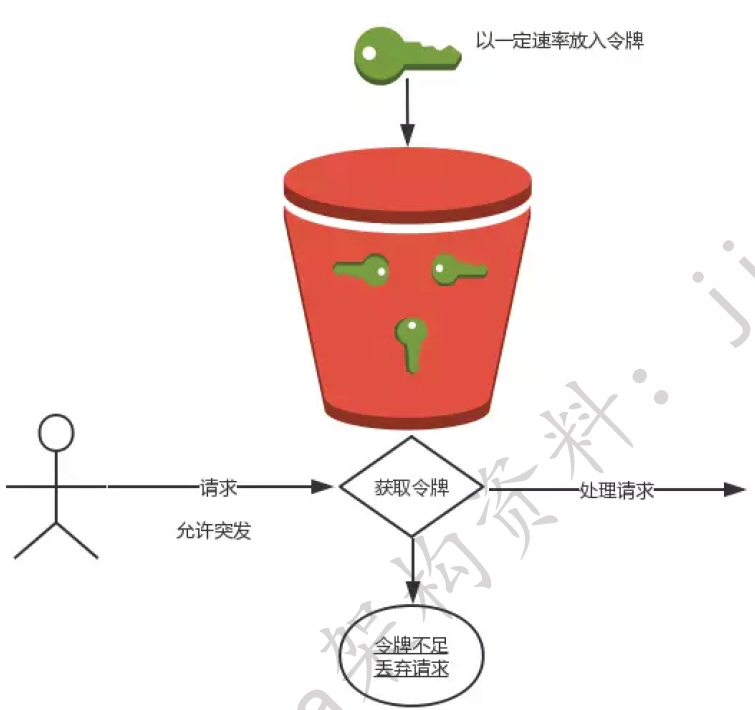
在秒杀活动中,用户的请求速率是不固定的,这里我们假定为10r/s,令牌按照5个每秒的速率放入令牌桶,桶中最多存放20个令牌。仔细想想,是不是总有那么一部分请求被丢弃。
计数器 VS 滑动窗口
计数器算法是最简单的算法,可以看成是滑动窗口的低精度实现。滑动窗口由于需要存储多份的计数器(每一个格子存一份),所以滑动窗口在实现上需要更多的存储空间。也就是说,如果滑动窗口的精度越高,需要的存储空间就越大。
漏桶算法 VS 令牌桶算法
漏桶算法和令牌桶算法最明显的区别是令牌桶算法允许流量一定程度的突发。因为默认的令牌桶算法,取走token是不需要耗费时间的,也就是说,假设桶内有100个token时,那么可以瞬间允许100个请求通过。
令牌桶算法由于实现简单,且允许某些流量的突发,对用户友好,所以被业界采用地较多。当然我们需要具体情况具体分析,只有最合适的算法,没有最优的算法。