本文大量参照 David E. Rumelhart, Geoffrey E. Hinton and Ronald J. Williams, Learning representation by back-propagating errors, Nature, 323(9): 533-536, 1986.
在现代神经网络中, 使用最多的算法当是反向传播(BP). 虽然BP有着收敛慢, 容易陷入局部最小等缺陷, 但其易用性, 准确度却是其他算法无可比拟的.
在本文中, $w_{ji}$为连接前一层$unit_{i}$和后一层$unit_{j}$的权值.
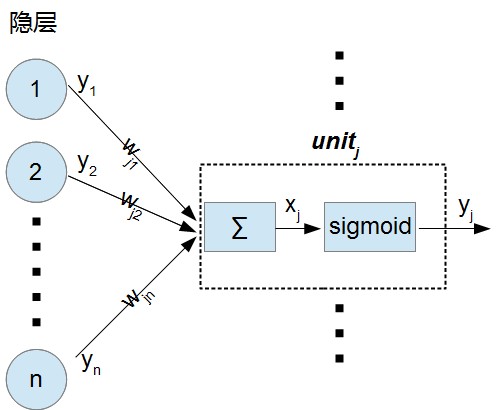
在MLP中, 对于输出层神经元$unit_{j}$, 它的输入$x_{j}$按下式进行计算(忽略偏置):
$x_{j} = sum_{i} y_{i} w_{ji}$
可以看到它的输入等于前一层所有神经元的输出$y_{i}$和对应连接的加权和, 如上图
而$unit_{j}$的输出按下式计算:
$y_{j} = frac{1}{1+e^{-x_{j}}}$. 这就是一个非线性变换sigmoid,
对于有监督训练, 期望输出$d$和实际输出$y$现在都是已知的, 定义误差为:
$E=frac{1}{2}sum_{c} sum_{j}(y_{j,c}-d_{j,c})^2$
其中的$c$是输入-输出样本对的标号, $j$是输出层神经元的标号.
为求出$partial E/partial w_{ji}$,
我们先求$partial E/partial y_{j}$(之后就知道为何如此):
$partial E/partial y_{j} = y_{j} - d_{j}$, 此为误差$E$对神经元$unit_{j}$输出的偏导.
由链式法则:
$partial E/partial x_{j} = partial E/partial y_{j} * d y_{j}/d x_{j}$, 及上面的输入输出的关系式
$d y_{j}/d x_{j} = (frac{1}{1+e^{-x_{j}}})' = frac{e^{-x_{j}}}{(1+e^{-x_{j}})^{2}} = y_{j} * (1-y_{j})$
我们可以求出误差$E$对$unit_{j}$的输入$x_{j}$的偏导:
$partial E/partial x_{j} = partial E/partial y_{j} * y_{j} * (1-y_{j})$
至此, 我们得到了误差$E$对于$unit_{j}$输入$x_{j}$的偏导, 但网络训练的是权值(偏置), 所以我们必须知道$E$对于$w_{ji}$的偏导表达式.
同样由链式法则:
$partial E/partial w_{ji} = partial E/partial x_{j} * partial x_{j}/partial w_{ji}$, 及本层输入和权值的关系式:
$x_{j} = sum_{i} y_{i} w_{ji}$, 可得 $partial x_{j}/partial w_{ji} = y_{i}$, 即:
$partial E/partial w_{ji} = partial E/partial x_{j} * y_{i}$,
其中$y_{i}$为前一层神经元$unit_{i}$的输出, $y_{j}$为后一层神经元$unit_{j}$的输出.
为了处理中间层, 我们同样是按照链式法则, 对于第i个神经元, 我们可以求得误差$E$对其输出$y_{i}$的梯度(注意这里是$y_{i}$, 不是$y_{j}$):
$partial E/partial y_{i} = partial E/partial x_{j} * partial x_{j}/partial y_{i} = partial E/partial x_{j} * w_{ji}$,
考虑到第i个神经元的所有连接, 可以得到:
$partial E/partial y_{i} = sum_{j}partial E/partial x_{j} * w_{ji}$ (1)
这里的$partial E/partial x_{j}$为误差对于后一层的神经元$unit_{j}$输入$x_{j}$的偏导.
我们梳理一下:
对于连接神经元$i$和神经元$j$的权值$w_{ji}$, 主要有3个偏导分子, 输入$x_{j}$, 输出$y_{j}$和权值$ w_{ji}$, 他们的关系如下:
$partial E/partial x_{j} = partial E/partial y_{j} * y_{j} * (1-y_{j})$ (2)[基于$y_{j}$和$x_{j}$的非线性转换关系式];
$partial E/partial w_{ji} = partial E/partial x_{j} * y_{i}$ (3)[基于$x_{j}$和$y_{i}$的加权求和公式].
为求得上面的式(3), 我们需要求得$partial E/partial x_{j}$, 而为求得$partial E/partial x_{j}$, 需要求得$partial E/partial y_{j}$.
对于输出层(最后一层), $partial E/partial y_{j}=y_{j} - d_{j}$;
对于中间层, $partial E/partial y_{i}$按式(1)进行计算, 而式(1)中的$partial E/partial x_{j}$是由$partial E/partial y_{j}=y_{j} - d_{j}$算出来的. 当我们算出中间层的$partial E/partial y_{i}$之后, 把式(2)中的$y_{j}$全部替换成$y_{i}$就可以计算出$partial E/partial x_{i}$从而计算出式(3), 注意此时的式(3)中的$y_{i}$应该变为第i个神经元的前一层的对应神经元.
如此迭代, 我们就可以更新所有的权值啦.
权值调整的公式如下:
$delta w = -epsilon partial E/partial w$
总结:
BP的精髓: 如何通过链式法则求出$partial E/partial w_{ji}$
求法:
注意, 以下推导, 统一使用$i$ 作为当前层前一层的神经元下标, $j$ 作为当前层的神经元下标, $k$ 作为后一层神经元下标.
对于最后一层:
$partial E/partial w_{ji} = partial E/partial x_{j} * partial x_{j}/partial w_{ji}$ (1)
其中,
$partial E/partial x_{j} = partial E/partial y_{j} * partial y_{j}/partial x_{j}$ (2)
$partial x_{j}/partial w_{ji} = y_{i}$ (3, 已求出, 谢谢背锅侠指正)
式(2)中,
$ partial E/partial y_{j} = y_{j} - d_{j}$ (已求出)
$ partial y_{j}/partial x_{j} = y_{j} * (1 - y_{j})$ (已求出)
从而计算出误差对[最后一层到倒数第二层的权值]的梯度.
$partial E/partial w_{ji} = ( y_{j} - d_{j}) * y_{j} * (1 - y_{j}) * y_{i}$
对于倒数第二层:
唯一变化的只有 $ partial E/partial y_{j} $ 的求法. 同样适用链式法则展开:
$ partial E/partial y_{j} = partial E/partial y_{k} * partial y_{k}/partial y_{j}$, 其中 $y_{k}$ 为后一层(最后一层)的第$k$个神经元输出.
由于$partial E/partial y_{k} = y_{k} - d_{k}$(非固定, 每层表达式取前一层计算结果),
而$partial y_{k}/partial y_{j} = partial y_{k}/partial x_{k} * partial x_{k}/partial y_{j}$,
其中 $partial y_{k}/partial x_{k} = y_{k} * (1 - y_{k})$ (固定的, 每层表达式都一样)
$partial x_{k}/partial y_{j} = w_{kj}$ (固定的, 每层表达式都一样)
故$partial y_{k}/partial y_{j} = y_{k} * (1 - y_{k}) * w_{kj}$ (固定的, 每层表达式都一样)
从而有 $ partial E/partial y_{j} = partial E/partial y_{k} * y_{k} * (1 - y_{k}) * w_{kj}$ (非固定, 用于下一层的误差梯度计算)
最终: $partial E/partial w_{ji} = partial E/partial y_{j} * y_{j} * (1 - y_{j}) * y_{i}$
倒数第三层
可将倒数第二层求出的的$partial E/partial y_{j}$作为本层的$partial E/partial y_{k}$, 可计算出 $partial E/partial y_{j}$, 从而计算出 $partial E/partial w_{ji}$.