排序（冒泡排序、快速排序)

基本排序分类图：

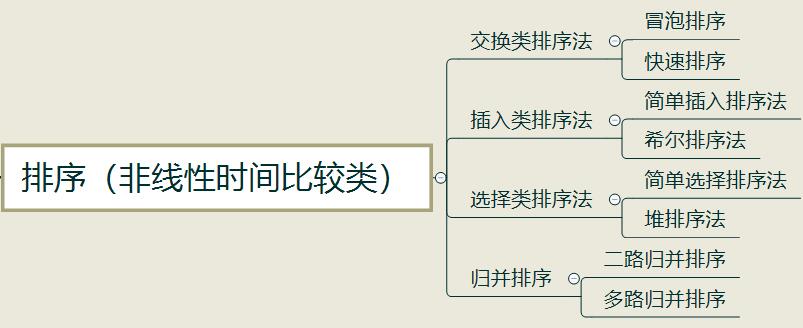
关于排序的稳定性

在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。

一、 冒泡排序

冒泡排序的基本思想：每次比较两个相邻的元素，如果它们的顺序错误就把他们交换过来

冒泡排序的原理：每一趟只能确定将一个数归位，如果有n个数进行排序，只需将n-1个数归位，也就是说要进行n-1趟操作，而每一趟都需要从第1位开始进行相邻两个数的比较

#include <stdio.h>
#define MAX 7

int main(void)
{
    int i, j, t;
    int a[MAX] = {1, 5, 3, 7, 6, 4, 2};
    
    //冒泡排序核心部分
    for (i = 0; i < MAX - 1; i++) //n个数排序只需要n-1趟
    {
        for (j = 0;j < MAX - i; j++) //每一趟比较到n-i结束
        {
            if (a[j] < a[j + 1])//降序排列
            {
                t = a[j];
                a[j] = a[j + 1];
                a[j + 1] = t;
    
            }
        }
    }
    for (i = 0; i < MAX; i++)
    {
        printf("%d ", a[i]);
    }

    return 0;
}

 冒泡排序的核心部分是双重嵌套循环，冒泡排序的时间复杂度是O(N²)，这个一个非常高的时间复杂度

冒泡排序的优化：

当第i次冒泡排序一次都没有交换，说明该序列已经变成有序的了，这样就减少了比较次数（注意是比较次数，不是交换次数），代码如下：

#include <stdio.h>
#define MAX 7

int main(void)
{
    int i, j, t;
    int flag = 0;
    int n = 0;
    int a[MAX] = {1, 5, 3, 7, 6, 4, 2};
    
    //冒泡排序核心部分
    for (i = 0; i < MAX - 1; i++) //n个数排序只需要n-1趟
    {
        flag = 0;
        for (j = 0;j < MAX - i; j++) //每一趟比较到n-i结束
        {
            n++;
            if (a[j] < a[j + 1])
            {
                t = a[j];
                a[j] = a[j + 1];
                a[j + 1] = t;
                flag = 1;
            }
        }
        if (flag == 0)    /* 一次交换都没有，说明已经是有序序列*/
        {
            break;    /* 跳出整个循环 */
        }
    }
    for (i = 0; i < MAX; i++)
    {
        printf("%d ", a[i]);
    }
    printf("
比较次数%d
", n);

    return 0;
}

优化前：

优化后：

 二、快速排序

快速排序是基于二分的思想，对冒泡排序的一种改进

快速排序基本思想：

通过一趟排序将要排序的数据分割成独立的两部分：分割点左边都是比它小的数，右边都是比它大的数。然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

快速排序原理：第一步：设置两个指针left和right分别指向数组的头部和尾部，并且以头部的元素（6）为基准数

　　　　　　　第二步：right指针先往左移动，找到小于基准数的元素就停下，然后移动left指针（想一下为什么是right先移动，不能是left先移动）

　　　　　　　第三步：left指针往左移动，找到大于基准数的元素就停下，然后交换right和left指针所值元素的值

　　　　　　　重复第二、三步，直到两个指针left和right重合

　　　　　　　第四步：两个指针重合后将基准数（6）与两个指针指向的元素值（3）交换

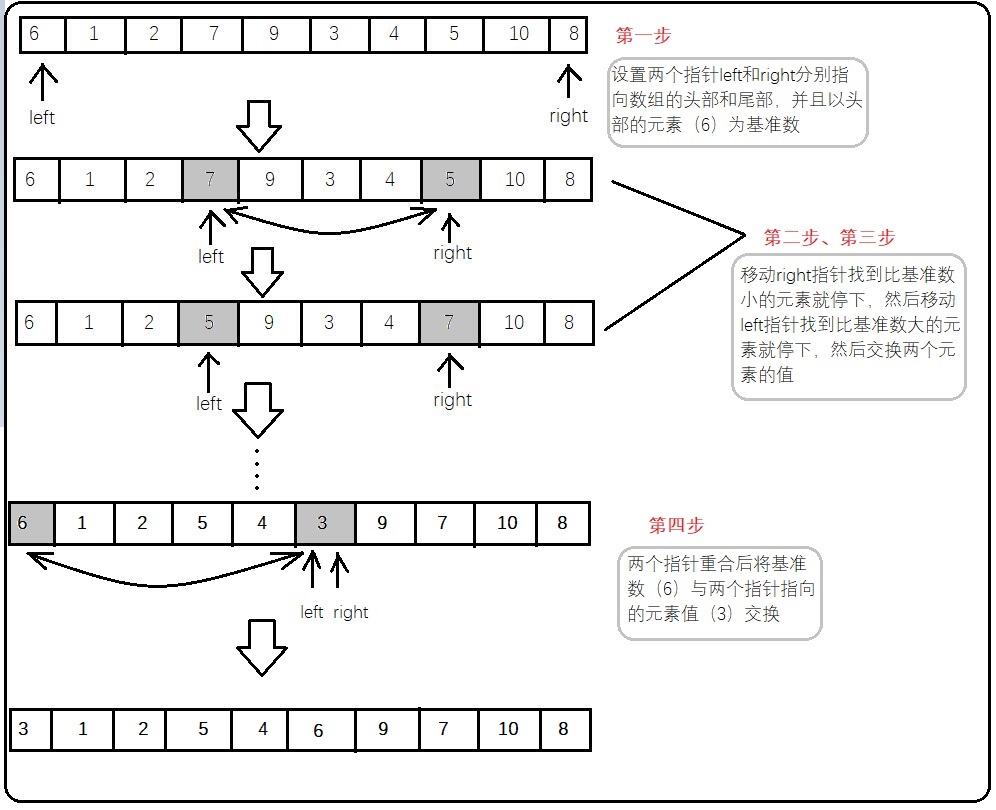
 到这时，第一轮排序结束，此时以基准数（6）为分界点，（6）左边的数都小于等于6，（6）右边的数都大于等于6，现在我们已经将原来的序列以（6）为分界点拆成了两个序列

左边的序列是3 1 2 5 4，右边的序列是9 7 10 8，接下来分别处理这两个序列，因为处理方法与上图相同，下面就不上图了（摸个鱼）

先处理3 1 2 5 4，以（3）为基准数，处理后结果为2 1 3 5 4

再处理（3）左边的数2 1，以（2）为基准数，处理后为1 2

再处理（3）右边的数5 4，以（5）为基准数，处理后为4 5

现在的序列为1 2 3 4 5 6 9 7 10 8，现在对9 7 10 8进行处理

因为处理方式与上面相同这里不再赘述，处理结果为7 8 9 10

最终序列为1 2 3 4 5 6 7 8 9 10，到此排序完全结束（快速排序的每一轮处理其实就是将这一轮的基准数归位，直到所有的数都归位为止）

#include <stdio.h>
void quicksort(int left, int right, int *a);

#define N 7
int main(void)
{
    int i;
    int a[N] = {5, 1, 7, 2, 4, 3, 6};

    quicksort(0, N-1, a);

    for(i = 0; i < N; i++)
    {
        printf("%d ", a[i]);
    }

    return 0;
}
void quicksort(int left, int right, int *a)
{
    int i, j, t, temp;
    if (left > right) //基线情况
    {
        return;
    }

    temp = a[left]; //存入基准数
    i = left;
    j = right;
    while (i != j)
    {
        //先从右往左找
        while (a[j] >= temp && j>i)
        {
            j--;
        }
        //从左往右找
        while (a[i] <= temp && j>i)
        {
            i++;
        }

        if (i < j)
        {
            t = a[i];
            a[i] = a[j];
            a[j] = t;
        }
    }
    a[left] = a[i]; //基准数归位
    a[i] = temp;

    quicksort(left, i - 1, a);
    quicksort(i + 1, right, a);
    
    return;
}

快速排序在最坏的情况下，仍可能是相邻的两个数进行交换，因此快速排序最差时间复杂度和冒泡排序是一样的，都是O(N²)，它的平均时间复杂度为O（NlogN）