介绍
BP神经网络属于多层前向神经网络,BP网络是前向网络的核心部分,也是整个人工神经网络体系的精华,广泛应用于分类识别、逼*、回归、压缩等领域。
BP神经网络采用误差反向传播(Error Back Propagtion,BP)的学习算法。一个包含2层隐层的BP神经网络的拓扑结构如下图所示:
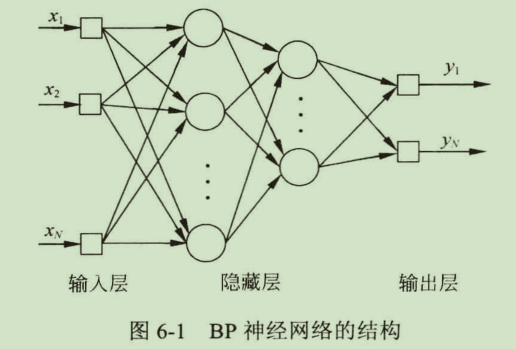
BP神经网络特点
- BP网络由多层构成,层与层之间全连接,同一层之间的神经元无连接。多层的设计,使得BP网络可以从输入中挖掘更多的信息,完成更复杂的任务。
- BP网络的传递函数必须可微。一般使用Sigmoid函数或者线性函数作为传递函数。根据输出值是否包含负值,Sigmoid函数又可以分为Log-Sigmoid函数和Tan-Sigmoid函数。Log-Sigmoid函数由
 确定:
确定:
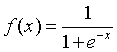
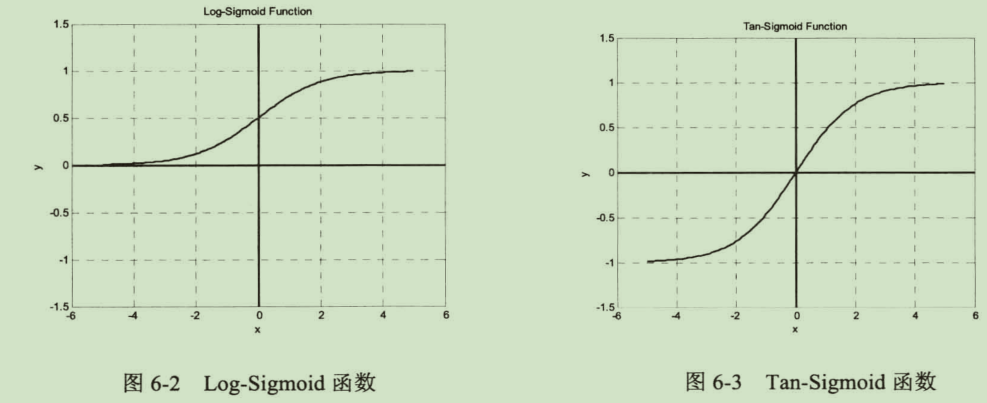
BP网络的典型设计是隐含层采用Sigmoid函数作为传递函数,而输出层采用线性函数作为传递函数。
- 采用误差反向传播算法进行学习。训练网络权值时,沿着减小误差的方向,从输出层经过中间各层逐层向前修正网络的连接权值,随着学习的进行,误差越来越小。
BP网络学习算法
最速下降法基于这样的原理:对于实值函数F(x),如果F(x)在某点x0处有定义且可微,则函数在该点处沿着梯度相反方向下降最快。
![]()
最速下降法的缺陷:
1.目标函数必须可微
2.如果最小值附*比较*坦,则算法会在最小值附*停留很久,收敛缓慢。可能出现“之”字形下降
3.算法可能陷入局部极小值,而没有达到全局最小值点
BP网络权值调整规则可以总结为:
![]()
BP网络的复杂性在于隐含层与隐含层之间、隐含层与输入层之间调整权值时,局部梯度的计算需要用到上一步计算的结果。也正是此原因,BP网络学习时,只能从后向前依次进行计算。
最速下降BP法的改进
标准的最速下降法在实际应用中往往有收敛速度慢的缺点,几种标准BP算法的改进如下:
动量BP法

学习率可变的BP算法
学习率可变的BP算法通过观察误差的增减来判断,当误差以减小的方式趋于目标值时,说明修正方向是正确的,可以增加学习率;当误差超过一定范围时,说明前一步修正的不正确,应该减小步长,并撤销前一步修正的结果,学习率的增减通过一个增量/减量因子实现:
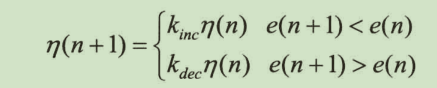
拟牛顿法
LM(Levenberg-Marquardt算法)
设计BP网络的方法
- 网络层数
BP网络可以包含一个到多个隐含层,对于大部分应用场合,单个隐含层即可满足需要。
- 输入层节点数
输入层节点数取决于输入向量的维数
- 隐含层节点数
隐含层节点数对BP网络的性能有很大影响,一般较多的隐含层节点数可以带来更好的性能,但可能导致训练时间过长。通常采用经验公式给出估计值:

- 输出层神经元个数
- 传递函数的选择
一般隐含层使用Sigmoid函数,而输出层采用线性函数。
- 训练方式的选择
- 初始权值的确定
初始值过大或者过小都会对性能产生影响,通常将初始权值定义为较小的非零随机值,经验值为(-2.4/F,2.4/F)或者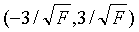 之间,其中F为权值输入端连接的神经元个数。
之间,其中F为权值输入端连接的神经元个数。
BP网络相关函数
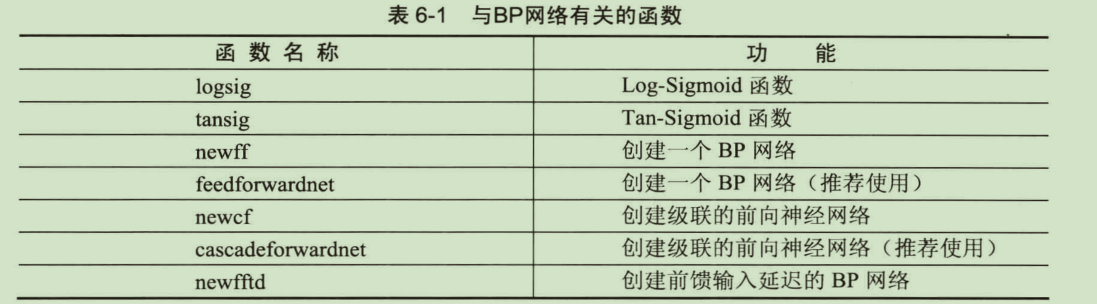
神经网络应用实例
某学院共有260名学生,其中男生172人,女生88人,统计学生的身高和体重,部分数据如表所示:
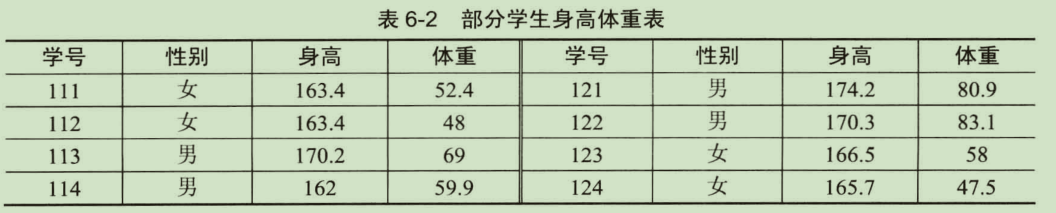
本例将260个样本随机抽出一部分作为训练样本,训练一个BP神经网络,剩下的作为测试样本输入网络进行测试。
getdata.m 读取样本数据
function [data,label]=getdata(xlsfile) % [data,label]=getdata('student.xls') % read height,weight and label from a xls file [~,label]=xlsread(xlsfile,1,'B2:B261'); [height,~]=xlsread(xlsfile,'C2:C261'); [weight,~]=xlsread(xlsfile,'D2:D261'); data=[height,weight]; l=zeros(size(label)); for i=1:length(l) if label{i}== '男' l(i)=1; end end label=l;
divide.m 将样本数据随机分为训练数据和测试数据
function [traind,trainl,testd,testl]=divide(data,label) % [data,label]=getdata('student.xls') %[traind,trainl,testd,testl]=divide(data,label) % 随机数 % rng(0) % 男女各取30个进行训练 TRAIN_NUM_M=30; TRAIN_NUM_F=30; % 男女分开 m_data=data(label==1,:); f_data=data(label==0,:); NUM_M=length(m_data); % 男生的个数 % 男 r=randperm(NUM_M); traind(1:TRAIN_NUM_M,:)=m_data(r(1:TRAIN_NUM_M),:); testd(1:NUM_M-TRAIN_NUM_M,:)= m_data(r(TRAIN_NUM_M+1:NUM_M),:); NUM_F=length(f_data); % 女生的个数 % 女 r=randperm(NUM_F); traind(TRAIN_NUM_M+1:TRAIN_NUM_M+TRAIN_NUM_F,:)=f_data(r(1:TRAIN_NUM_F),:); testd(NUM_M-TRAIN_NUM_M+1:NUM_M-TRAIN_NUM_M+NUM_F-TRAIN_NUM_F,:)=f_data(r(TRAIN_NUM_F+1:NUM_F),:); % 赋值 trainl=zeros(1,TRAIN_NUM_M+TRAIN_NUM_F); trainl(1:TRAIN_NUM_M)=1; testl=zeros(1,NUM_M+NUM_F-TRAIN_NUM_M-TRAIN_NUM_F); testl(1:NUM_M-TRAIN_NUM_M)=1;
main_newff.m
% 脚本 使用newff函数实现性别识别 % main_newff.m %% 清理 clear,clc rng('default') rng(2) %% 读入数据 xlsfile='student.xls'; [data,label]=getdata(xlsfile); %% 划分数据 [traind,trainl,testd,testl]=divide(data,label); %% 创建网络 net=feedforwardnet(3); %指定隐含层为1层,节点数为3 net.trainFcn='trainbfg'; %采用拟牛顿法对应的训练函数trainbfg进行训练 %% 训练网络 net=train(net,traind',trainl); %% 测试 test_out=sim(net,testd'); test_out(test_out>=0.5)=1; test_out(test_out<0.5)=0; rate=sum(test_out==testl)/length(testl); fprintf(' 正确率 %f %% ', rate*100);