poj 2411 Mondriaan's Dream 状态压缩dp

Description

Squares and rectangles fascinated the famous Dutch painter Piet Mondriaan. One night, after producing the drawings in his 'toilet series' (where he had to use his toilet paper to draw on, for all of his paper was filled with squares and rectangles), he dreamt of filling a large rectangle with small rectangles of width 2 and height 1 in varying ways.

Expert as he was in this material, he saw at a glance that he'll need a computer to calculate the number of ways to fill the large rectangle whose dimensions were integer values, as well. Help him, so that his dream won't turn into a nightmare!

Input

The input contains several test cases. Each test case is made up of two integer numbers: the height h and the width w of the large rectangle. Input is terminated by h=w=0. Otherwise, 1<=h,w<=11.

Output

For each test case, output the number of different ways the given rectangle can be filled with small rectangles of size 2 times 1. Assume the given large rectangle is oriented, i.e. count symmetrical tilings multiple times.

Sample Input

1 2
1 3
1 4
2 2
2 3
2 4
2 11
4 11
0 0

Sample Output

1
0
1
2
3
5
144
51205

求w*h(1<=w,h<=11)的方块中，铺满1*2砖块的铺法数量，限时3s。

我之前做过类似的题目：http://www.cnblogs.com/lastone/p/5261548.html

那道题的数据范围是(1<=n<=5  1<=m<=10^9)，总的来看poj这道题更简单。

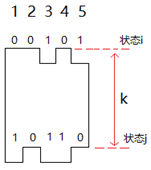
看上图w为5的情况，先不管h是多少，定义dp[i][j]表示首部是状态i，尾部是状态j且k为1的铺砖方案数，dp数组可以用一次dfs得到。然后定义ret[k][j]表示首部压缩状态为0，尾部是状态j的方案数，就可以得到：

$$ret[k][j]=sum_{i=0}^{1<<w} {sum_{j=0}^{1<<w}}ret[k][j]=ret[k-1][i]*dp[i][j] $$

k循环从1~h，其意义和图中的k一致，最终的答案便是ret[h][0]。

这里计算一组数据(w,h)的复杂度应该是：$O(h*2^w*2^w)$

最好预处理打表，因为在运算过程中，还可以顺便计算出其它输入数据的结果，比如计算w=10,h=11时，就能顺便计算出所有w=10的所有情况。

所以我的方法是对所有w=1~11，h=11这11组数据进行预处理就能把所有答案输出出来。

但是这样超时了-_-，本地跑不到2s，交上去就超时了。

于是想着怎样进行优化。

分析：程序计算过程有一些是重复了的，比如(w=1,h=3)和(w=3,h=1)，根据刚才的复杂度公式，应尽量避免w较大值的计算，所以把w=11的所有情况舍去，因为在之前已经有(w=1,h=11)、(w=2,h=11)、(w=3,h=11)……(w=10,h=11)的计算。而至于(w=11,h=11)的情况特殊对待为0就行了。

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
using namespace std;
typedef long long ll;
ll dp[1<<11][1<<11];
ll dd[1<<11][1<<11][11];
int m,n;
void dfs(int col,int pre,int now)
{
    if(col>n) return;
    if(col==n)
    {
        dp[pre][now]++;
        return;
    }
    dfs(col+1,pre<<1,(now<<1)|1);
    dfs(col+1,(pre<<1)|1,now<<1);
    dfs(col+2, pre<<2 , now<<2);
}
ll ret[2][1<<11];
ll ans[12][12];
int main()
{
    memset(ans,0,sizeof(ans));
    for(n=10;n>=1;n--)
    {
        m=11;
        memset(dp,0,sizeof(dp));
        dfs(0,0,0);
        ans[n][1]=ans[1][n]=dp[0][0];
        memset(ret,0,sizeof(ret));
        int t=0;
        for(int i=0;i<(1<<n);i++) {
            ret[0][i]=dp[0][i];
        }

        for(int k=1; k<m; k++)
        {
            t=!t;
            for(int i=0; i<(1<<n); i++) {
                ret[t][i] = 0;
                for(int j=0; j<(1<<n); j++)
                    ret[t][i]+=ret[!t][j]*dp[j][i];
            }
            ans[n][k+1]=ans[k+1][n]=ret[t][0];
        }
    }
    while(scanf("%d%d",&m,&n)!=EOF&&m&&n)
    {
        printf("%I64d
",ans[n][m]);
    }
}

时间：2016 MS