在一张2021× 2021的表格中,初始时所有格子都是白色的.甲挑选了两个格子涂黑,接下来每一步我们都需要将所有至少与一个黑格子有公共边的格子找出来并同时涂黑.已知甲挑选的两个黑格子满足我们可以通过最少的步骤将所有格子都涂黑,请问我们一共进行了多少步涂黑的操作?
经分析可知,两个黑格子导致的染色可看作独立的、互不影响的过程。令两个黑格子为A、B,其坐标分别为x1 y1 、 x2 y2,则对于坐标为x y的格子,易知其被A、B染黑的步数分别为 |x-x1|+|y-y1|、|x-x2|+|y-y2|,则全部染黑需要的步数为 max(min(|xi-x1|+|yi-y1|、|xi-x2|+|yi-y2|)),i=1,2···2021*2021。
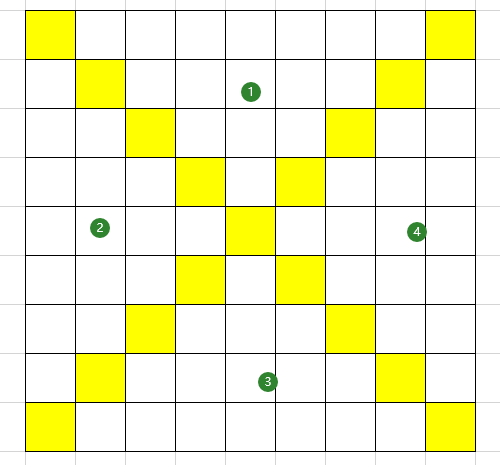
两个黑格子不能在上图的黄格上,因为如果有在黄格上的话,最终步数肯定大于等于2020。而我可以找到步数小于2020的方式。而且两个黑格只能在对立的区域(13、24),不然步数>=2020。
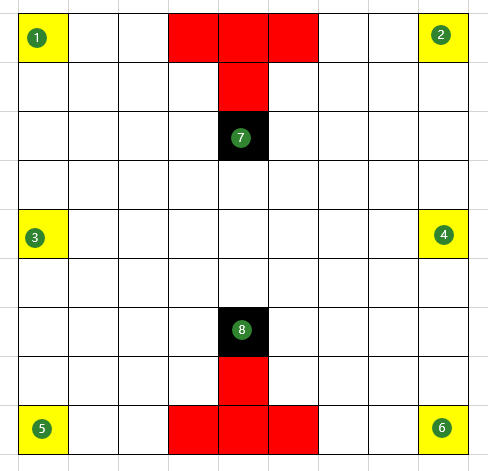
当黑格如上图所示时,步数为1515。下面证明最少步数就是1515。由之前分析可知1、2,5、6肯定由7、8分别染黑,假设最少步数小于1515,那么1、2、5、6的步数肯定小于1515,那么黑格必然在红色区域内。而所有的红格与3、4的距离都大于1515,所以最小步数大于1515,矛盾,所以最小步数就是1515.