date:20210520
No:1025
title:除数博弈
description:爱丽丝和鲍勃一起玩游戏,他们轮流行动。爱丽丝先手开局。 最初,黑板上有一个数字 N 。在每个玩家的回合,玩家需要执行以下操作: 选出任一 x,满足 0 < x < N 且 N % x == 0 。 用 N - x 替换黑板上的数字 N 。 如果玩家无法执行这些操作,就会输掉游戏。 只有在爱丽丝在游戏中取得胜利时才返回 True,否则返回 False。假设两个玩家都以最佳状态参与游戏。
解题方法:
- 动态规划
- 归纳法
解题思路:
- 动态规划:
- 最后一个数字(即n)的状态和前一个因数的状态有关————(解释:爱丽丝轮到的因数会一步一步导致结果,那么我们倒过来,从前往后推,从爱丽丝轮到因数1和2开始推(因为二者是已知的))
- 保存爱丽丝会轮到所有因数的状态(也就是说保存爱丽丝在每一个因数处的结果,以供下一个因数查询————记忆化查询)
- 归纳法:
- 数学方法,本专题主要记录动态规划,所以在此不赘述其他方法,官方有给题解,可以去leetcode看看
实现代码:
- 本题使用python3:
class Solution:
def divisorGame(self, n: int) -> bool:
target = [0 for i in range(n+1)]
target[1] = 0
if n <= 1:
return False
else:
target[2] = 1 # 若爱丽丝抽到2,则爱丽丝赢
for i in range(3,n+1):#因为(3,n)不包括n所以用n+1
for j in range(1,i//2):
if i%j==0 and target[i-j]==0:
target[i] = 1
return target[n] == 1
- 动态规划法通过截图:
date:20210521
No:剑指offer No.42
title: 连续子数组的最大和
description:输入一个整型数组,数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。 要求时间复杂度为O(n)。
解题方法:
- 动态规划
- 暴力
解题思路:
- 动态规划:
- 构建动态规划数组,每一个格子记录以当前位置为结尾的最大连续序列的和,然后遍历完之后找dp数组中最大的数字,即为答案
- 暴力:
- 这没啥说的,遍历,以每个位置为结尾在嵌套一个遍历,把所有的可能都列出来,然后找最大的(简略的说了下,主题是动态规划,在此不再赘述)
实现代码:
- 本题使用java:
public int maxSubArray(int[] nums) {
int[] dp = new int[nums.length];
Arrays.fill(dp,Integer.MIN_VALUE);
dp[0] = nums[0];
for(int i = 1;i<nums.length;++i){
dp[i] = Math.max(dp[i-1]+nums[i],nums[i]);
}
int res = Integer.MIN_VALUE;
for (int i : dp) {
res = Math.max(i,res);
}
return res;
}
- 通过截图
date:20210522
No:764
title: 使用最小花费爬楼梯
description:数组的每个下标作为一个阶梯,第 i 个阶梯对应着一个非负数的体力花费值 cost[i](下标从 0 开始)。 每当你爬上一个阶梯你都要花费对应的体力值,一旦支付了相应的体力值,你就可以选择向上爬一个阶梯或者爬两个阶梯。 请你找出达到楼层顶部的最低花费。在开始时,你可以选择从下标为 0 或 1 的元素作为初始阶梯。
解题方法
- 剪枝
- 动态规划
解题思路:
-
剪枝:通过递归模拟走楼梯,然后计算走一步和走两步的最小值,最后通过一个过渡数组记录经过的点的最优解,防止再次递归到这个点的时候重复计算,走楼梯过程如下图,会有重复的节点树
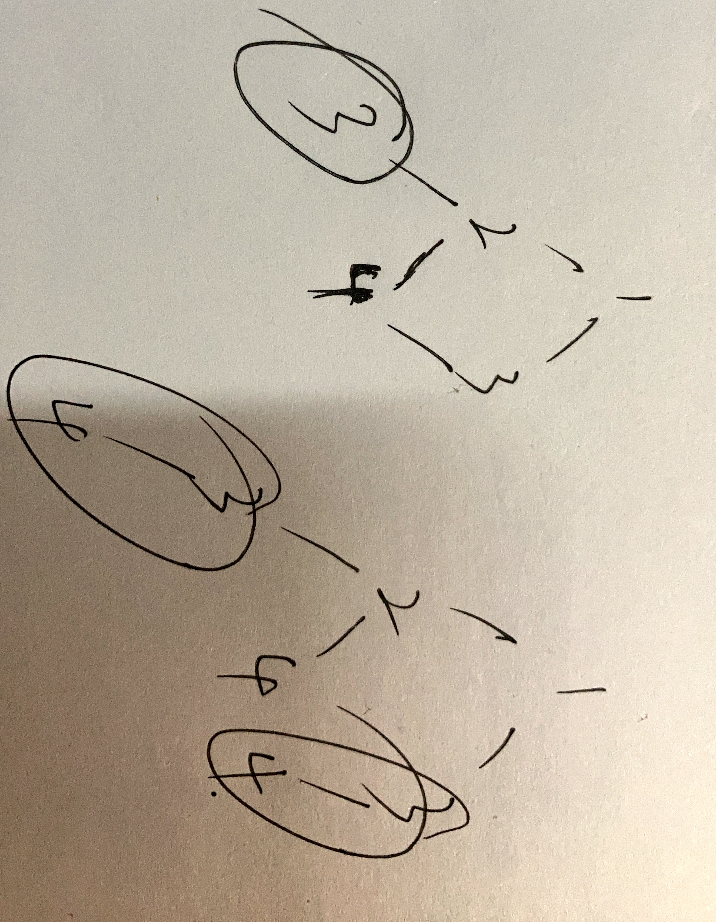
-
动态规划:动态规划的核心就是记忆化搜索,所以定义一个dp数组,每个格子保存当前到位置的最小消耗,最后返回倒数两个节点中的小值即可
实现代码
- 剪枝:
package algorithm;
import java.util.Arrays;
public class MinCostClimbingStairs {
private static int[] dp;
public static int minCostClimbingStairs(int[] cost) {
dp = new int[cost.length+1];
Arrays.fill(dp,0);
minCostClimbingStairs(cost,-1,dp);
return dp[0];
}
private static int minCostClimbingStairs(int[] cost,int index,int[] dp){
if(index>=cost.length){
return 0;
}
int temp = index ==-1?0:cost[index];
if(dp[index+1]!=0) {
return dp[index+1];
}
int one = minCostClimbingStairs(cost, index + 1, dp);
int two = minCostClimbingStairs(cost, index + 2, dp);
dp[index+1] = Math.min(one + temp, two + temp);
return dp[index+1];
}
public static void main(String[] args) {
int[] cost = {1, 100, 1, 1, 1, 100, 1, 1, 100, 1};
System.out.println(minCostClimbingStairs(cost));
}
}
- 动态规划:
class Solution {
public int minCostClimbingStairs(int[] cost) {
for(int i = 2;i<cost.length;++i){
cost[i] += Math.min(cost[i-1],cost[i-2]);
}
return Math.min(cost[cost.length-1],cost[cost.length-2]);
}
}
通过截图
date:20210523
No:面试题 17.16
title: 按摩师
description:一个有名的按摩师会收到源源不断的预约请求,每个预约都可以选择接或不接。在每次预约服务之间要有休息时间,因此她不能接受相邻的预约。给定一个预约请求序列,替按摩师找到最优的预约集合(总预约时间最长),返回总的分钟数。 注意:本题相对原题稍作改动
解题方法:
- 动态规划
解题思路:
- 动态规划:
- 设计一个dp数组,每一个格子保存以当前位置结尾的最大预约时间(可以不包含当前位置预约),最后返回最后一个格子即可;保存策略就是,对比nums[i]+dp[i-2]和dp[i-1]的大小,保存大的值,一次遍历之后,最后一个格子保存的就是整个序列中最大的预约时间
实现代码
- 本题使用的语言是python3
class Solution:
def massage(self, nums: List[int]) -> int:
if len(nums)<=0: return 0
if len(nums)==1: return nums[0]
dp = []
dp.append(nums[0])
dp.append(max(nums[0],nums[1]))
for i in range(2, len(nums)):
dp.append(max((dp[i-2]+nums[i]),dp[i-1]))
return dp[-1]
通过截图
date:20210524
No:329
title: 判断子序列
description:给定字符串 s 和 t ,判断 s 是否为 t 的子序列。 字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde"的一个子序列,而"aec"不是)。 进阶: 如果有大量输入的 S,称作 S1, S2, ... , Sk 其中 k >= 10亿,你需要依次检查它们是否为 T 的子序列。在这种情况下,你会怎样改变代码?
解题方法:
- 双指针
- 动态规划
解题思路:
- 双指针:在s和t上各安排一个指针,然后遍历t,只要s的对应字符等于t当前位置字符,s的指针加一,如果s的指针到达末尾,则说明s为t的子序列,就返回true,否则如果一个循环都未返还,说明s中有t中不存在的字符,返回false
- 动态规划:还是那句话,动态规划的核心是记忆化搜索,我们只要维护一个二维数组,记录从第i(t上)个字符开始,下一个字符(26个字母)出现的位置,遍历s时查询t就可以线性化,复杂度为O(1),至于dp数组,从后面开始遍历记录就好;
实现代码
- 双指针:
class Solution {
public boolean isSubsequence(String s, String t) {
if(s.equals("")) return true;
if(s.length()>t.length()) return false;
int index_s = 0;
char temp = s.charAt(index_s);
for(int i = 0;i<t.length();++i){
if(temp==t.charAt(i)){
index_s++;
if(index_s==s.length()) return true;
temp = s.charAt(index_s);
}
}
return false;
}
}
- 动态规划:
class Solution {
public boolean isSubsequence(String s, String t) {
if(s.length()>t.length()) return false;
if(s.length()==0)return true;
int n = s.length();
int m = t.length();
int[][] dp = new int[m+1][26];//记录每一个字符开始下一个字符的位置
for (int[] ints : dp) {
Arrays.fill(ints,m);
}
for(int i = m-1;i>=0;--i){
for(int j = 0;j<26;++j){
if(t.charAt(i)==j+'a'){
dp[i][j] = i;//说明该字符在当前位置出现
}else{
dp[i][j] = dp[i+1][j];//继承上一个状态
}
}
}
int next = 0;
for(int i = 0;i<n;++i){
if(dp[next][s.charAt(i)-'a']==m){//说明该字符不会出现
return false;
}else{
next = dp[next][s.charAt(i)-'a']+1;
}
}
return true;
}
}
通过截图
-
双指针:
-
动态规划:
date:20210525
No:1641
title: 统计字典序元音字符串的数目
description:给你一个整数 n,请返回长度为 n 、仅由元音 (a, e, i, o, u) 组成且按 字典序排列 的字符串数量。 字符串 s 按 字典序排列 需要满足:对于所有有效的 i,s[i] 在字母表中的位置总是与 s[i+1] 相同或在 s[i+1] 之前。
解题方法:
- 动态规划
解题思路:
- 还是那句话:动态规划的核心就是记忆化搜索以及实时更新记忆,该题有如下规律(别的博客学来的,我太菜了/大哭):

实现代码:
- 本体使用java语言
class Solution {
public int countVowelStrings(int n) {
int[] dp = {1,1,1,1,1};
for(int i = 1;i<n;++i){
for(int j = 3;j>=0;--j){
dp[j] += dp[j+1];
}
}
int sum = 0;
for (int i : dp) {
sum += i;
}
return sum;
}
}
通过截图:

date:20210528
No:1314
title:矩阵区域和
description:给你一个 m x n 的矩阵 mat 和一个整数 k ,请你返回一个矩阵 answer ,其中每个 answer[i][j] 是所有满足下述条件的元素 mat[r][c] 的和: · i - k <= r <= i + k, · j - k <= c <= j + k 且 · (r, c) 在矩阵内。
解题方法
- 动态规划(记忆化搜索||二维前缀和)
解题思路:
- 动态规划:我们算的res矩阵实质上是在求原矩阵各种的区域和,如果我们能把每个前缀的和记录下来,那么在计算res矩阵的时候,就可以靠这个矩阵(后面称为dp矩阵)来记忆化搜索,可以节省大量时间(如果直接计算区域和,则每次需要算k*k次),具体如图示

实现代码
- 本题使用java实现
class Solution {
public int[][] matrixBlockSum(int[][] mat, int k) {
int[][] res = new int[mat.length][mat[0].length];
int[][] dp = new int[mat.length][mat[0].length];
for (int i = 0; i < dp.length; ++i) {
for(int j = 0;j<dp[0].length;++j){
dp[i][j] = (j>=1?dp[i][j-1]:0) + mat[i][j];
}
for(int j = 0;j<dp[0].length;++j){
dp[i][j] += (i>=1?dp[i-1][j]:0);
}
}
for(int i = 0;i<res.length;++i){
for(int j = 0;j<res[0].length;++j){
int temp1 = (i+k>= res.length?res.length-1:i+k);
int temp2 = (j+k>= res[0].length?res[0].length-1:j+k);
int temp3 = i-k-1;
int temp4 = j-k-1;
res[i][j] = dp[temp1][temp2] - (temp3<0?0:dp[temp3][temp2])
- (temp4<0?0:dp[temp1][temp4]) + (temp3<0||temp4<0?0:dp[temp3][temp4]);
}
}
return res;
}
}
通过截图
date:20210616
No:5
title:最长回文子串
description:给你一个字符串 s,找到 s 中最长的回文子串
解题方法
- 动态规划(记忆化搜索)
解题思路
- 动态规划:将字符串的每个字字符串是否为回文串记录下来,这样搜索的时候复杂度就是O(1),而暴力搜索最耗费时间的就是判断字符串是否为回文串(普通方法就是遍历所有可能,然后每一个字符串都通过一次判断方法,这样花销太大)
实现代码
- 本题使用java语言实现
class Solution {
public String longestPalindrome(String s) {
if(s.length()==1||s.length()==0)return s;
boolean[][] dp = new boolean[s.length()][s.length()];
//2到8是否为回文串,charAt(2) == charAt(8) && dp[3][7]
//1到3是否为回文串,charAt(1)==charAt(3)&& dp[2][2]
for(int i = 0;i<s.length();++i){
dp[i][0] = true;
}
Arrays.fill(dp[s.length()-1],true);
for(int i = s.length()-2;i>=0;--i){
for(int j = 1;j<s.length();++j){
dp[i][j] = i>=j?true:((s.charAt(i) == s.charAt(j)) && dp[i+1][j-1]);
//填充dp数组,将字符串的状态保存
}
}
//for(int i = 0;i<dp.length;++i){
//for(int j = 0;j<dp.length;++j){
//System.out.print(dp[i][j]);
//}
//System.out.println();
//}
int res_i = -1;//表示最长回文序列的起始坐标
int res_j = -1;//表示最长回文序列的末尾坐标
int sum = 0;//表示最长回文序列的长度
for(int i = 0;i<s.length();++i){
for(int j = s.length()-1;j> i ;--j){
int temp = j-i;
if(dp[i][j]&&temp>sum){
res_i = i;
res_j = j;
sum = temp;
//System.out.println(res_i);
//System.out.println(res_j);
//System.out.println(sum);
}
}
}
if(res_j==-1)return s.charAt(0)+"";
return s.substring(res_i,res_j+1);
}
}
通过截图
