嗯好的今天我们来谈谈cosplay
splay是一种操作,是一种调整二叉排序树的操作,但是它并不会时时刻刻保持一个平衡,因为它会根据每一次操作把需要操作的点旋转到根节点上
所谓二叉排序树,就是满足对树中的任意一个节点,它左子树上的任意一个值比它的值小,右子树上的任意一个值比它的值大的一棵二叉树 ;至于平衡:是一棵空树或任意节点的左右两个子树的深度差的绝对值不超过1(from:百度百科) 看图:
不平衡:
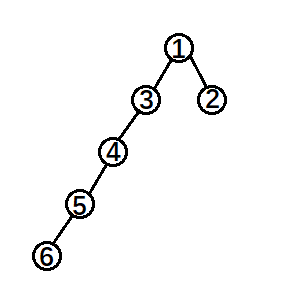
平衡:
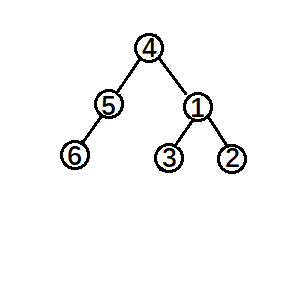
可以观察到这两棵树都是满足⑥<⑤<④<③<①<②的大小关系,只是改变每个点的相对位置不同。
然后呢,splay的真正含义就出来了:通过很多很多次变换把要处理的点放到根节点上。与此同时,我们把这种变换叫做旋转。旋转的精髓就是在不破坏树中的大小顺序的同时改变节点的位置。旋转是splay的核心(虽然大部分排序树的核心操作都是旋转),大概思路和treap是差不多的(没学过treap然后爆发出狂笑),但对于splay相对来说懒一点的是它转的时候是自动判断左旋还是右旋。每一次旋转,我们把被旋转的这个点向上转一层(也就是转到它父节点的位置上)
比如说要旋转⑤节点:

可以看看旋转之后的样子:

因为⑤<④<③,所以要把⑤旋转后应该是③的左子树(也就是④的位置),但是⑧始终是大于④的所以⑧的位置是不变的 (④的右子树),然后因为⑤<⑦<④,所以④和⑦都应该是⑤的右子树而且⑦应该是④的左子树(因为是一棵二叉树),然后可以发现与⑥,⑧没有任何关系,真正改变的就只有图中的红线(表示各个节点间的父子关系)。这就是旋转的步骤。
但如果⑤是④的右子树呢?其实是差不多的,就是左右翻转一下。再想想这个图,自己推一遍:
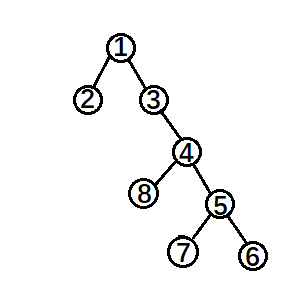
好的,那么旋转的普遍规律就可以看出来了:整个旋转的操作中改变的只是被旋转点、它的父节点、以及它的某一棵子树,到底是哪一棵子树是根据被旋转点与它父亲的关系来决定的:如果这个点是它父节点的左子树,那么应该调整这个点的右子树;如果是右子树,则相反。
(有两个很棒的动图来表示旋转)
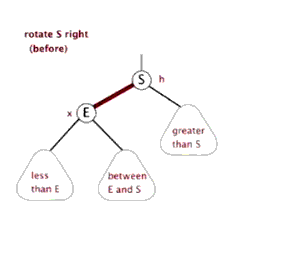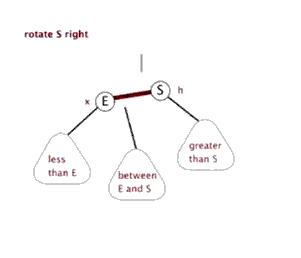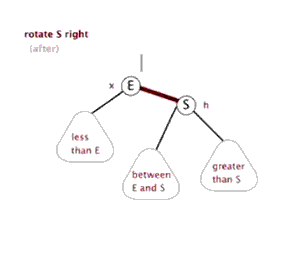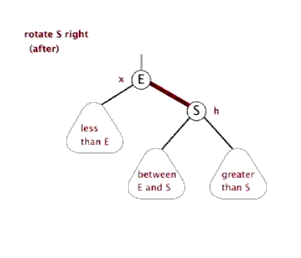
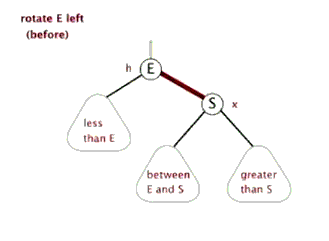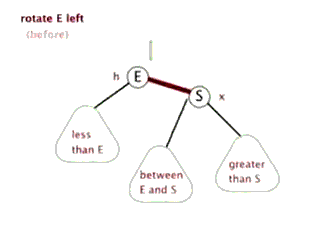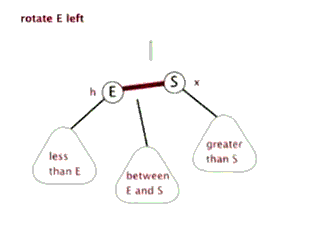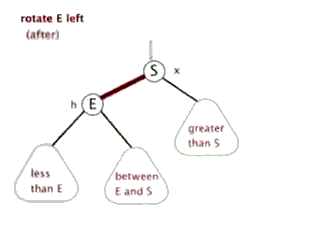
接下来打出代码。在那之前,我们先定义数组:
son[i][0]是指点i的左节点编号,son[i][1]是右节点编号
root表示当前根节点的编号
sz是指整个树的值的种数,同时用于新节点插入时的编号(可以类比时间戳)
siz[i]表示以i为顶点的树的值的个数,要计算重复出现的值(包括i节点自己)
key[i]表示节点i的值是多少
fa[i]表示节点i的父节点编号
cnt[i]表示节点i的值出现了多少次(数量cnt,siz[i]和种类sz是两个东西不要搞混了)
因为旋转的方式是由它是左子树还是右子树决定的,所以我们可以先写一个函数来判断:
int get(int x){
return son[fa[x]][1]==x;//如果它父节点的右儿子编号等于它那么返回1(右节点),否则返回0(是左节点)
}
接下来就是旋转了:
void rotate(int x){
int f=fa[x],ff=fa[f],w=get(x);//父节点、祖父节点、是父节点的左子树还是右子树
son[f][w]=son[x][w^1];//x节点的另一个子树放给原本x节点的位置
fa[son[f][w]]=f;//更新x节点的另一个子树的父节点
son[x][w^1]=f;//将父节点接到x节点的另一个子树上
fa[f]=x;
fa[x]=ff;//f、x位置互换后更新祖父节点
if(ff){//父节点不是根节点(根节点的父节点为0)
son[ff][son[ff][1]==f]=x;
}
update(f);
update(x);
}
注意这里的^位运算,意思是两位不同时返回1,相同时返回0,这里^1可以快速找出另一个儿子(0^1=1,1^1=0)
这里的update是指旋转之后由于位置的改变而引起的种类总数的变化,因为每一个节点值的出现的次数是没有改变的,其实很简单就是左子树种类加上右子树种类:
void update(int x){
if(x!=0){//如果是根节点,旋转时种类数始终不变
siz[x]=cnt[x];//自身值的出现次数
if(son[x][0])//如果有左子树
siz[x]+=siz[son[x][0]];
if(son[x][1])//如果有右子树
siz[x]+=siz[son[x][1]];
}
}
这只是一次操作,我们前面说了我们是把要处理的点旋转到根节点上,那么怎么做呢?循环就行了。但是还有一种特殊情况,由于这种情况都满足被旋转点和父节点都是左节点或者是右儿子,我们姑且称它为三点一线,先看图:
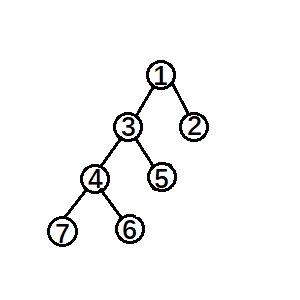
比如说我们这里要splay④,如果直接把④一直旋转到根节点的话就会是这样:

可以看见③还是①的左节点,相当于只是改变了④和①的关系,专业一点就是说形成了单旋使平衡树失衡。而解决的方法就是在出现三点一线时先旋转它的父节点避免单旋,正确的应该是这样: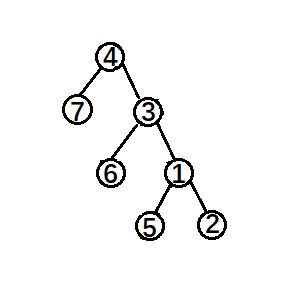
void splay(int x){
for(int f;f=fa[x];rotate(x)){//注意旋转的始终是x
if(fa[f]){//可能存在三点一线
rotate(get(x)==get(f)?f:x);//三点一线情况判断
}
}
root=x;//旋转完成后更新root的值
}
接下来是splay的插入:由于在旋转的时候,我们是建立在这棵树是有序的前提下的,而要保证这个前提,就需要从这棵树的建立开始就让它有序,所以,我们在插入的时候就必须按照排序树的规定来插入,也就是说每次插入都是从根节点开始比较大小,直到找到这个值或者是找到树的底部(这个值没有出现过):
void insect(int v){
if(sz==0){//如果这棵树是空树,插入点应该为根节点
sz++;
son[1][1]=son[1][0]=fa[1]=0;
siz[1]=cnt[1]=1;
root=1;
key[1]=v;
return;
}
int now=root,f=0;//now表示现在查找到节点编号,f表示当前节点的父节点
while(1){
if(key[now]==v){//如果这个值已经在树中,那么它出现的次数增加
cnt[now]++;
update(now);//更新相关点
update(f);
splay(now);//将插入的点旋转到根节点,便于下一次可能的操作
break;
}
f=now;
now=son[now][v>key[now]];//依照节点值查找位置,如果大于当前值v>key[now]=1,则在右子树范围内,反之亦然
if(now==0){//树中无这个值,查找到树的底端,新建一个子节点
sz++;//新节点编号
son[sz][1]=son[sz][0]=0;//新节点初始化
fa[sz]=f;
siz[sz]=cnt[sz]=1;
son[f][v>key[f]]=sz;//判断新节点是它父节点的左节点还是右节点并更新父节点
key[sz]=v;
update(f);//更新数量
splay(sz);//旋转到根节点
break;
}
}
}
接下来是查找一个值在树中排从小到大第几(是比它小的有多少个)(如果为了方便理解也可以说是从大到小求倒数第几),原理很简单,因为排序树的性质,我们可以知道只要是在这个节点的左边的都是比它小的,那么我们就可以利用之前记录好的siz来快速求出:(注意是数量,要加上重复的,比如说1,2,2,3,这个数列中,3排第4)
int find(int v){
int ans=0,now=root;//ans记录已经有多少比它小的点,now表示正在寻找的节点的编号
while(1){
if(v<key[now]){//如果当前节点的值大于v,那么当前节点的左子树不完全小于v,继续向当前节点的左子树寻找
now=son[now][0];
}
else{//当前节点的左子树上的值必然全部小于v
ans+=(son[now][0]!=0?siz[son[now][0]]:0);//如果有左子树则直接加上左子树的数量
if(v==key[now]){//如果当前节点的值等于v,则右子树上不可能有比它小的数,所有比它小的数已经找完
splay(now);//下一次可能的操作
return ans+1;//有1个数比它小那么它应该是第2,以此类推,要+1
}
ans+=cnt[now];//key[now]<v的情况,除了它的左儿子还要加上它自身的数量
now=son[now][1];//右子树中可能存在比v小的值,所以在右子树中继续寻找
}
}
}
有了查找排名,如果需要知道第几是多少,也是可以求的:
int findx(int x){
int now=root;//当前节点
while(1){
if(son[now][0]!=0&&siz[son[now][0]]>=x){//如果左子树的数量大于x,就是说第x个是在左子树上(前提是有左子树)
now=son[now][0];//在左子树上接着搜索
}
else{//第x个在以当前节点为顶点的树中
int less=(son[now][0]!=0?siz[son[now][0]]:0)+cnt[now];//左子树的数量(可能没有)+当前节点的值的数量
if(x<=less)//由于之前判断过是否在左子树上,并且在之后的运算中排除了所有左子树,x却不在右子树上,那么只可能是当前点的值
return key[now];
x-=less;//在右子树中还有多少值比它小,排除左子树
now=son[now][1];//继续搜索
}
}
}
接下来是前驱,就是指比它小的第一个点(就是比它自己的值小而且它的前驱与它自己的值的差的绝对值最小)。在树中表现为它的左子树中最右边的那个点,这样才满足比它自身的值小并且最接近它自身的值:
int query_pre(int x){
splay(x);//首先旋转到根节点方便查找
int now=son[root][0];//定位左子树
while(son[now][1]!=0)now=son[now][1];//循环查找左子树中最右边的点
return now;//最底部跳出循环,找到答案
}
有前驱当然也有后继,类似的,后继是指比它大的第一个点(比它自己的值大而且它的后继与它自己的值的差的绝对值最小)。在树中表现为它右子树最左边的那个点:(原理一模一样)
int query_next(int x){
splay(x);
int now=son[root][1];
while(son[now][0]!=0)now=son[now][0];
return now;
}
Last but not the least:删除。这里的删除是删除一次值,就是说受cnt的影响,不一定是删一个节点。这个挺复杂的,比如说删除一个值v,首先我们用之前的find(v)将值等于v的点旋转到根上,之后要分5种情况:
- 这个值出现了不止一次:直接减少次数,更新数量即可;
- 整棵树只剩下它一个值 孤苦伶仃 :将树清空;
- 这个点没有左子树:直接将右子树的顶点提出来,取代它的父节点;
- 这个点没有右子树:直接将左子树的顶点提出来,取代它的父节点;
- 这个点左右子树都有:先把前驱为作新树的根(叫做新根)(后继也完全没有问题,只是之后的处理要想一想是左子树还是右子树),将它旋转到根,这个时候在将原根的右儿子接到新根的左儿子上,更新即可。
这里先给出清空:(就是把所有关于这个点的东西归零)
void clear(int x){
son[x][0]=son[x][1]=fa[x]=siz[x]=key[x]=cnt[x]=0;
}
接下来就可以开始删除了:
void del(int v){
find(v);
if(cnt[root]>1){//第一种情况
cnt[root]--;
update(root);
return;
}
if(son[root][0]==0&&son[root][1]==0){//第二种情况
clear(root);
root=0;//将树清空
return;
}
if(son[root][0]==0){//第三种情况
int old=root;
root=son[root][1];
fa[root]=0;//新根的父节点更新
clear(old);
return;
}
if(son[root][1]==0){//第四种情况
int old=root;
root=son[root][0];
fa[root]=0;
clear(old);
return;
}
int newroot=query_per(root),oldroot=root;
splay(newroot);//将新根转上来
fa[son[oldroot][1]]=newroot;
son[root][1]=son[oldroot][1];//继承右子树
clear(oldroot);//旧根归零
update(root);//更新新根
}