zoukankan      html  css  js  c++  java

  • 为什么我要放弃javaScript数据结构与算法（第九章）—— 图

    本章中，将学习另外一种非线性数据结构——图。这是学习的最后一种数据结构，后面将学习排序和搜索算法。

    第九章 图

    图的相关术语

    图是网络结构的抽象模型。图是一组由边连接的节点（或顶点）。学习图是重要的，因为在任何二元关系都可以用图来表示。

    任何社交网络都可以用图来表示。

    我们还可以用图来表示道路、航班以及通信状态

    道路

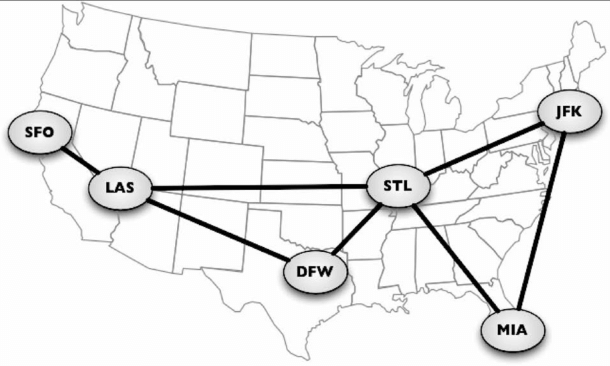
    一个图 G= （V,E）由以下元素组成。

    • V：一组顶点
    • E：一组边。连接V中的顶点

    道路

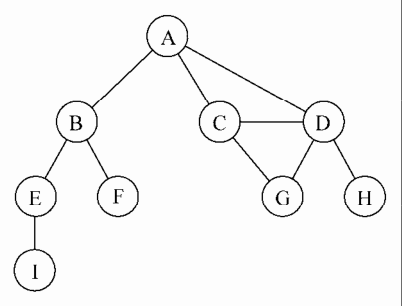
    由一条边连接在一起的顶点称为相邻顶点。比如，A和B 是相邻的，A和D是相邻的，A和C是相邻的，A和E是不相邻的。

    一个顶点的度是其相邻顶点的数量。比如，A和其他三个顶点相连接，因此，A的度为3；E和其他两个顶点相连接，因此E的度为2.

    路径是顶点v1,v2,...vk的一个连续序列，其中 vi 和 vi+1 （下标）是相邻的。以上一示意图为例，其中包含的路径A B E I 和 A C D G。

    简单路径要求不包含重复的顶点。举个例子，A D G是一条简单路径。除去最后一个顶点（因为它和第一个顶点是同一个顶点），环也是简单路径，比如A D C A（最后一个顶点重新回到A）

    如果途中不存在环则称该图是无环的。如果图中每两个顶点间都存在路径，则该图是连通的。

    有向图和无向图

    图可以是无向的（边没有方向）或是有向的（有向图）。下图就是有向图。

    有向图

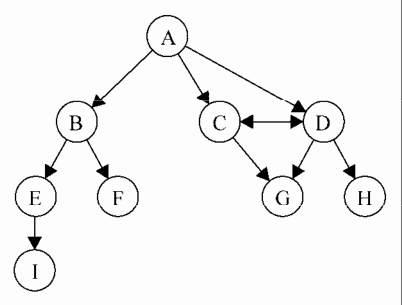
    有向图的边有一个方向。如果图中每两个顶点间在双向上都存在路径，则该图是强连通的。例如，C和D就是强连通的。图还可以是未加权的或者加权的。加权图的边被赋予了权值。

    加权图

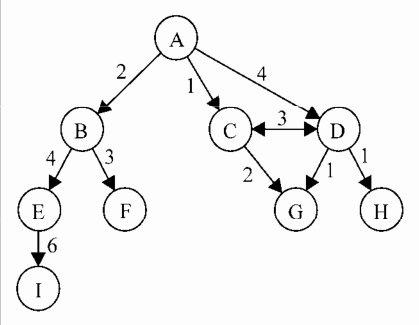
    我们可以使用图来解决计算机科学世界中的很多问题，比如搜索图中的一个特定顶点或搜索一条特定边，寻找图中的一条路径（从一个顶点到另一个顶点），寻找两个顶点之间的最短路径。

    图的表示

    从数据结构角度来说，我们有多种方式来表示图。在所有表示法中，不存在绝对正确的方法方式。图的正确表示法取决于解决的问题和图的类型。

    邻接矩阵

    图最常见的实现就是邻接矩阵。每个节点和一个整数相关联，该整数将作为数组的索引。我们用一个二维数组来表示顶点之间的连接。如果索引为i的节点和索引为 j的节点为邻，则 array[i][j] === 1,否则 array[i][j] === 0,如下图所示：

    邻接矩阵

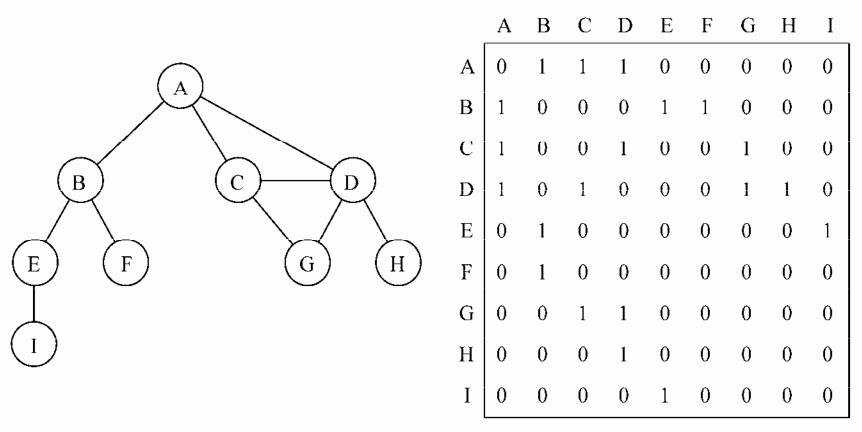
    不是强连通的图（稀疏图）如果用邻接矩阵来表示，则矩阵中将会有很多0，这意味着我们浪费了计算机存储空间来表示根本不存在的边。例如，找给定顶点的相邻顶点，即使该顶点只有一个相邻的顶点，我们也不得不迭代一整行。邻接矩阵表示法不够好的另一个理由是，图中顶点的数量可能会变化，而二维数组不太灵活。

    邻接表

    邻接表

    我们也可以使用一种叫做邻接表的动态数据来表示图。邻接表由图中每个顶点相邻顶点列表所组成。存在好几种方式来表示这种数据结构。我们可以用列表（数组）、链表，甚至是散列表或者是字典来表示相邻顶点列表。下面的示意图展示了邻接表等数据结构。

    邻接表

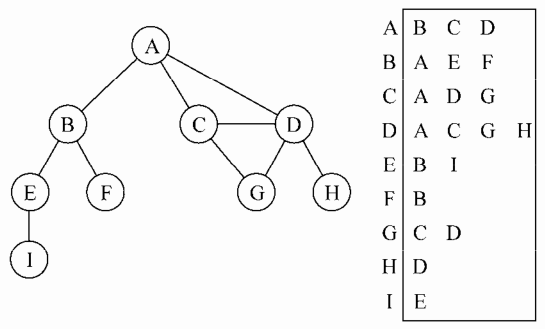
    尽管邻接表可能对大多数问题来说都是更好的选择，但以上两种表示法都有用，且它们有着不同的性质（例如，要找出顶点 v和w是否相邻，使用邻接矩阵会比较快）。在本章中，就会使用邻接表表示法。

    关联矩阵

    我们还可以用关联矩阵来表示图。在关联矩阵中，矩阵的行表示顶点，列表示边。如下图所示，我们使用二维数组来表示两者之间的连通性，如果顶点 v 是 边e的入射点，则 array[v][e] === 1,否则 array[v][e] === 0。

    关联矩阵

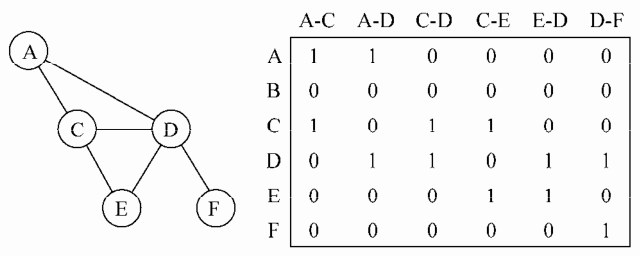
    创建 Graph 类

    我们先创建类的骨架

    function Graph(){
    var vertices = [];
    var adjList = new Dictionary();
}

    我们使用一个数组来存储图中所有顶点的名字，以及一个字典来存储邻接表。字典将会使用顶点的名字作为键，邻接顶点列表作为值。 vertices数组和 adjList字典两者都是我们 Graph类的私有属性。

    接着我们实现两个方法：一个用来向图中添加一个新的顶点（因为图实例化后是空的），另外一个方法用来添加顶点之间的边。我们先实现 addVertex 方法

    this.addVertex = function(v){
    vertices.push(v);
    adjList.set(v,[]);
}

    这个方法接受顶点 v 作为参数。我们将该顶点添加到顶点列表中，并且在邻接表中，设置顶点 v 作为键对应的字典值为一个空数组。

    实现 addEdge 方法

    this.addEdge = function(v,w){
    adjList.get(v).push(w);			
    adjList.get(w).push(v);			
}

    这个方法接受两个顶点作为参数。首先，通过将 w 加入到 v 的邻接表中，我们添加了一条自顶点 v 到顶点 w 的边。如果你想实现一个有向图，则（adjList.get(v).push(w)）就足够了。但是本章中大多数的例子都是基于无向图，我们需要添加一条自w向v的边。

    测试

    const graph = new Graph();
const myVertices = ['A','B','C','D','E','F','G','H','I'];
for(var i = 0; i < myVertices.length; i++){
    graph.addVertex(myVertices[i]);
}
graph.addEdge('A','B');
graph.addEdge('A','C');
graph.addEdge('A','D');
graph.addEdge('C','D');
graph.addEdge('C','G');
graph.addEdge('D','G');
graph.addEdge('D','H');
graph.addEdge('B','E');
graph.addEdge('B','F');
graph.addEdge('E','I');

    实现 Graph类的 toString 方法，便于在控制台输出图

    this.toString = function(){
    var s = '';
    for(var i = 0; i < vertices.length; i++){
        s += vertices[i] + ' -> ';
        var neighbors = adjList.get(vertices[i]);
        for(var j = 0; j < neighbors.length; j++){
            s += neighbors[j] + ' ';
        }
        s += '
';
    }
    return s;
}

    我们为邻接表表示法构建了一个字符串，首先迭代 vertices 数组列表，将顶点的名字加入字符串中，接着取得该顶点的邻接表，同样也迭代该邻接表，将相邻顶点加入我们的字符串。邻接表迭代完成后，给我们的字符串添加一个换行符。这样就可以在控制看到一个漂亮的输出了。

    A -> B C D 
B -> A E F 
C -> A D G 
D -> A C G H 
E -> B I 
F -> B 
G -> C D 
H -> D 
I -> E

    图的遍历

    和树数据结构相似，我们可以访问图的所有节点。有两种算法可以对图进行遍历：广度优先搜索（Breadth-First Search,BFS）和深度优先搜索（Depth-First Search,DFS）。图遍历可以用来寻找特定的顶点或者是寻找两个顶点之间的路径，检查图是否连通，检查图是否含有环等。

    图遍历算法的思想是必须追踪每个第一次访问的节点，并且追踪有哪些节点还没有被完全探索，对于两种图遍历算法，都需要明确指出第一个被访问的节点。

    完全探索一个顶点要求我们查看该顶点的每一条边。对于每一条边所连接的没有被访问过的顶点，将其标注为被发现的，并将其加入待访问的顶点。

    为了保证算法的效率，务必访问每个顶点至多两次。连通图中每条边和顶点都会被访问到。

    广度优先搜索算法和深度优先搜索算法基本上是相同的，只有一点不同，那就是待访问顶点列表的数据结构。

    算法 数据结构 描述
    深度优先搜索 栈 通过将顶点存入栈中，顶点是沿着路径被探索的，存在新的相邻顶点就去访问
    广度优先搜索 队列 通过将顶点存入队列，最先入队列的顶点先被探索

    当要标注已经访问过的顶点时，我们可以用三种颜色来放映它们的状态

    • 白色：表示该顶点还没有被访问
    • 灰色：表示该顶点被访问过，但是还没有探索过
    • 黑色：表示该顶点被访问过且被完全探索过

    广度优先搜索

    广度优先搜索算法会从指定的第一个顶点开始遍历图，会访问其所有相邻点，就像一次访问图的一层。换句话说，就是先宽后深地访问顶点，如下图所示

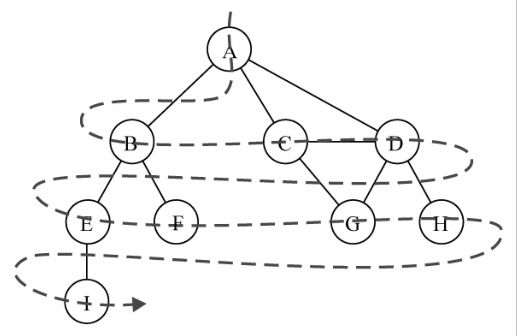
    广度优先搜索

    以下是从顶点 v 开始的广度优先搜索算法所遵循的步骤

    1. 创建一个队列 Q
    2. 将 v 标注为被发现的（灰色），并将 v 入队列Q
    3. 如果队列Q 非空，则运行以下步骤
      1. 将 u 从 Q 中出队列
      2. 将标注 u 为被发现的（灰色）
      3. 将 u 所有未被访问过的邻点（白色）入队列
      4. 将 u 标注为已被探索的（黑色）

    实现广度优先搜索算法

    // 颜色辅助-广度优先搜索算法
this.initializeColor = function(){
    var color = [];
    for(var i = 0; i < vertices.length; i++){
        color[vertices[i]] = 'white';
    }
    return color;
}	
// 广度优先搜索算法
this.bfs = function(v,callback){
    var color = this.initializeColor(),
    queue = new Queue();
    queue.enqueue(v);
    while(!queue.isEmpty()){
        var u = queue.dequeue(),
        neighbors = adjList.get(u);
        color[u] = 'grey';
        for(var i = 0; i < neighbors.length; i++){
            var w = neighbors[i];
            if(color[w] === 'white'){					
                color[w] = 'grey';
                queue.enqueue(w);
            }
        }
        color[u] = 'black';
        if(callback){
            callback(u)
        }
    }
}

    广度优先搜索和深度优先搜索多需要标注被访问过的顶点，为此，我们将使用一个辅助数组 color,由于当算法开始执行时，所有的顶点颜色都是白色，所以我们可以创建一个辅助函数 initializeColor 为这两个算法执行此初始化操作。

    我们要的第一件事情是用 initializeColor 函数来将 color 数组初始化为 white ,我们还需要声明和创建一个 Queue 实例，它将会存储待访问和待探索的顶点。

    bfs 方法接受一点顶点作为算法的起始点。起始顶点是必要的，我们将此顶点如队列。

    如果队列为空，我们将通过出队列操作从队列中移除一个顶点，并取得一个包含其所有邻点的邻接表。该顶点将被标注为 grey,表示我们已经发现了它（但还未被完全对其的探索）。

    对于 u 的每个邻点，我们取得其值，如果它还未被访问过，则将其标注了grey,并将这个顶点加入队列中，这样当从队列中出列的时候，我们可以完成对其的探索。

    当完全探索该顶点和及其邻点后，我们将标注该顶点为已探索过（黑色）。

    我们实现的这个 bfs 方法也接受一个回调。这个参数是可选的，如果我们传递了回调函数，会用到它。

    测试

    function printNode(value){
    console.log('访问了顶点：' + value);
}
graph.bfs(myVertices[0],printNode);

    得到下面的结果

    访问了顶点：A
访问了顶点：B
访问了顶点：C
访问了顶点：D
访问了顶点：E
访问了顶点：F
访问了顶点：G
访问了顶点：H
访问了顶点：I

    顶点访问顺序和之前的示意图所展示的一致。

    使用 BFS 寻找最短路径

    到目前为止，我们只展示了 BFS 算法的基本原理。我们可以用该算法做更多事情，而不只是输出被访问顶点的顺序。例如，考虑如何来解决下面的问题。

    给定一个图G和源顶点v，找出每个顶点u,u和v之间最短的路径（以边的数量计）

    对于给定顶点v，广度优化算法会访问所有与其距离为1的顶点，接着是距离为2的顶点，以此类推。所以，可以用广度优先算法来解决这个问题。我们可以修改bfs方法以返回给我们一些信息：

    • 从v到u的距离d[u]
    • 前溯点pred[u],用来推导出从v到其他每个顶点u的最短路径。

    实现：

    // 广度优先搜索算法优化版本
this.BFS = function(v){
    var color = this.initializeColor(),
    queue = new Queue(),
    d = [],
    pred = [];
    queue.enqueue(v);

    for(var i = 0; i < vertices.length; i++){
        d[vertices[i]] = 0;
        pred[vertices[i]] = null;
    }
    while(!queue.isEmpty()){
        var u = queue.dequeue();
        neighbors = adjList.get(u);
        color[u] = 'grey';
        for(var i = 0; i < neighbors.length; i++){
            // w相邻顶点
            var w = neighbors[i];
            if(color[w] === 'white'){
                color[w] == 'grey';
                d[w] = d[u] + 1;
                pred[w] = u;
                queue.enqueue(w);
            }
        }
        color[u] = 'black';
    }
    return {
        distance:d,
        predecessors: pred
    }
}

    首先需要声明数组 d 来表示距离，以及 pred 数组来表示前溯点。下一步用0来初始化数组d，把pred赋值为 null。

    当我们发现 顶点u的相邻点w时，则设置w的前溯点值为u。我们还通过给d[u]加1来设置顶点v和相邻点w之间的距离。

    方法的最后返回一个包含d和pred的对象。

    测试

    var shortestPathA = graph.BFS(myVertices[0]);
console.log(shortestPathA);
// distance: [A: 0, B: 1, C: 1, D: 2, E: 2, F: 2, G: 2, H: 3, I: 3]
// predecessors: [A: null, B: "A", C: "A", D: "C", E: "B", F: "B",G: "D", , H: "D", , I: "E"]

    通过前溯数组，我们可以用下面这段代码来构建从顶点A到其他顶点的路径：

    var fromVertex = myVertices[0];
for(var i = 1; i < myVertices.length; i++){
	var toVertex = myVertices[i],
	path = new Stack();
	for(var v = toVertex; v !== fromVertex;v = shortestPathA.predecessors[v]){
		path.push(v);
	}
	path.push(fromVertex);
	var s = path.pop();
	while(!path.isEmpty()){
		s += '-' + path.pop();
	}
	console.log(s);
}

    使用顶点A作为源顶点。对于每个其他顶点，我们会J计算顶点A到它的路径。我们从顶点数组得到toVertex ，然后会创建一个栈来 存储路劲值。

    接着，我们追溯 toVertext 到 fromVertext 的路径。变量v被赋值为前溯点的值。这样我们就可以方向追溯这条路径。将变量v添加到栈中。最后，源顶点也会被添加到栈中，以得到完整的路径。

    这之后，我们创建了一个s字符串，并将源顶点赋值给它。当栈是非空的时候，我们从栈中移出一个项并将其拼接到字符串s的后面。最后在控制台上输出路径。

    A-B
A-C
A-C-D
A-B-E
A-B-F
A-C-D-G
A-C-D-H
A-B-E-I

    深入学习的最短路径算法

    本章中的图不是加权图。如果要计算加权图中的最短路径（例如，城市A 和城市B之间的最短路径——GPS和Google Map 中用到的算法），广度优先搜索未必合适。

    举个栗子，Dijkstra 算法解决了单源中最短路径问题。Bellman-Ford 算法解决了边权值为负的单源最短路径问题。A*搜索算法解决了求仅一对顶点间的最短路径问题，它用经验法则来加速搜索过程。Floyd-Warshall算法解决了求所有顶点对间的最短路径的这一问题。

    图是一个广泛的主体，对最短路径及其变种问题，我们有很多的解决方案。

    深度优先搜索

    深度优先搜索算法将会从第一个指定的顶点开始遍历图，沿着路径直到这条路径最后一个顶点被访问了，接着原路返回并探索下一条路径。换句话说，它是先深度后广度地访问顶点，如下图所示

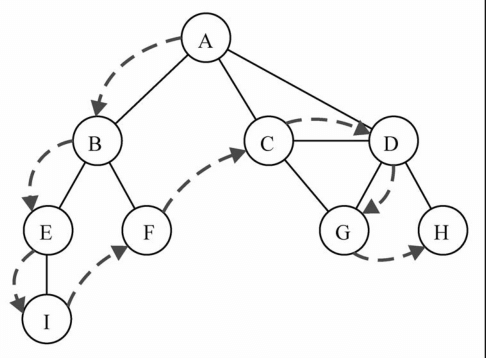
    深度优先搜索

    深度优先搜索算法不需要一个源顶点。在深度优先搜索算法中，若图中顶点v未被访问，则访问该顶点。

    要访问顶点v,照下列的步骤

    1. 标注v为被发现的（灰色）
    2. 对于v的所有未访问的邻点w，访问顶点w，标注v为已被探索的（黑色）

    实现

    // 深度优先探索算法
this.dfs = function(callback){
    var color = this.initializeColor();
    for(var i = 0 ; i < vertices.length; i++){
        if(color[vertices[i]] === 'white' ){
            this.dfsVisit(vertices[i],color,callback);
        }
    }		
}
this.dfsVisit =function(u,color,callback){
    color[u] = 'grey';
    if(callback){
        callback(u);
    }
    var neighbors = adjList.get(u);
    for(var i = 0 ;i < neighbors.length; i++){
        var w = neighbors[i];
        if(color[w] === 'white'){
            arguments.callee(w,color,callback);
        }
    }
    color[u] = 'black';
}

    首先，我们创建了颜色数组，并用值white 为图中的每个顶点对其进行了初始化，广度优先搜索也是这么做的。接着，对于图实例中每一个未被访问过的顶点，我们调用递归函数 dfsVisit ，传递的参数为顶点、颜色数组和回调函数。

    当访问u顶点时，我们标注其为被发现的grey。如果有callback 函数的话，则执行该函数输出已访问过的顶点。接下来一步是取得包含顶点u的所有邻点的列表。对于顶点u的每一个未被访问过的邻点w，我们将调用dfsVisit 函数，传递w和其他参数。最后，在该2顶点和邻点按深度访问之后，我们回退，意思是该顶点已经被完全探索了，并将其标注为black

    测试

    graph.dfs(printNode); 
// 访问了顶点：A
// 访问了顶点：B
// 访问了顶点：E
// 访问了顶点：I
// 访问了顶点：F
// 访问了顶点：C
// 访问了顶点：D
// 访问了顶点：G
// 访问了顶点：H

    下面这个示意图展示了该算法每一步的执行过程

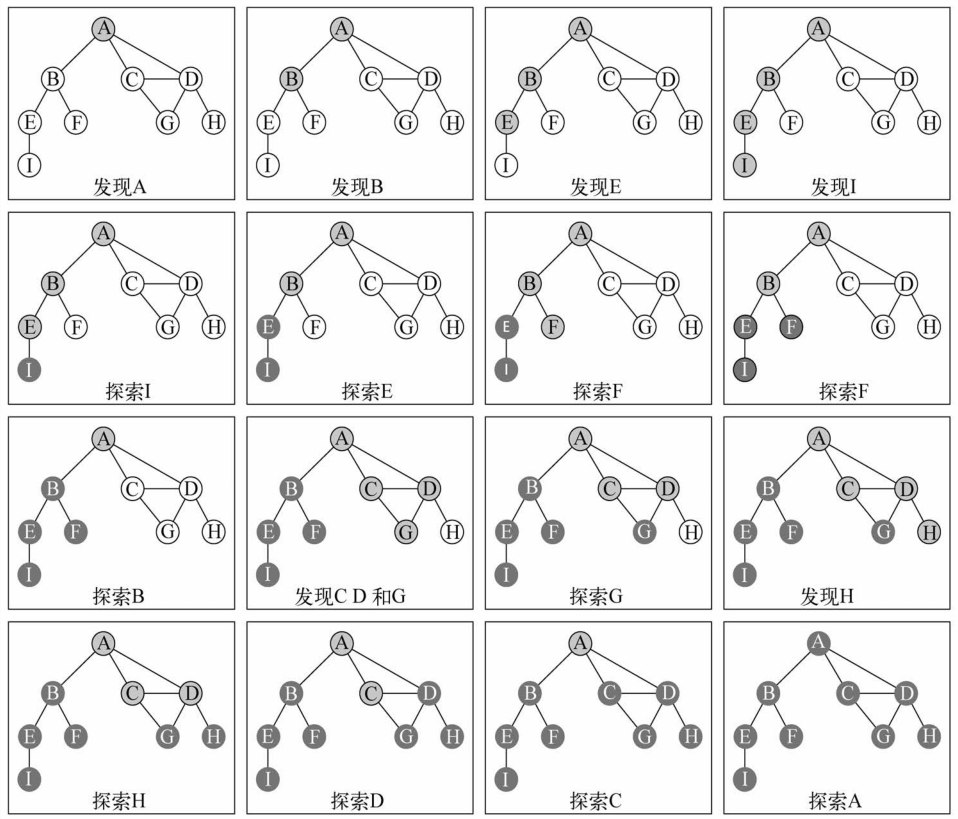
    深度优先搜索执行过程

    探索深度优化算法

    我们现在只是展示了深度优先搜索算法的工作原理。我们可以用该算法做更多的事情，而不是只输出被访问顶点的顺序。

    对于给定的图G，我们希望深度优先探索算法遍历图G的所有节点，构建“深林”（有根树的一个集合）已经一组源顶点（根），并输出两个数组:发现时间和完成探索时间。我们可以修改 dfs 方法来返回给我们一些信息：

    • 顶点u的发现时间d[u]
    • 当顶点u被标注为黑色时，u的完成探索时间f[u]
    • 顶点u的前溯点p[u]
    // 追踪发现事件和完成探索时间
var time = 0;
// 深度优先探索算法优化版本
this.DFS = function(){
    var color = this.initializeColor(),
    d = [],
    f = [],
    p = [];
    time = 0;

    for(var i = 0; i < vertices.length; i++){
        f[vertices[i]] = 0;
        d[vertices[i]] = 0;
        p[vertices[i]] = null;
    }

    for(i = 0; i< vertices.length; i++){
        if(color[vertices[i]] === 'white'){
            this.DFSVisit(vertices[i],color,d,f,p)
        }
    }
    return {
        discovery:d,
        finished:f,
        predecessors:p
    }
}
this.DFSVisit = function(u,color,d,f,p){
    console.log('发现了'+u);
    color[u] = 'grey';
    d[u] = ++time;
    var neighbors = adjList.get(u);
    for(var i = 0; i < neighbors.length; i++){
        var w = neighbors[i];
        if(color[w] === 'white'){
            p[w] = u;
            arguments.callee(w,color,d,f,p);
        }
    }
    color[u] = 'black';
    f[u] = ++time;
    console.log('探索了'+u);
}

    首先我们需要一个变量来追踪发现时间和完成探索时间。时间变量不能被作为参数传递，因为非对象的变量不能作为引用传递给其他Js方法。接下来，我们声明数组d、f和p。我们需要为图的每一个顶点来初始化这些数组。在这个方法结尾返回这些值。

    当一个顶点第一次被发现时，我们要追踪其发现时间。当它是由引自顶点u的边而被发现的。我们追踪它的前溯点。最后，当这个顶点被完全探索之后，我们追踪其完成时间。

    深度优先算法背后的思想是什么？

    边是从最近发现的u处被向外探索的。只有连接到未发现的顶点的边被探索了。当u所有的边都被探索了，该算法返回u被发现的地方去探索其他的边。这个过程持续到我们发现了虽偶有从原始顶点能够触及的顶点。如果还留有其他未被发现的顶点。我们对新的源顶点将重复这个过程。直到图中所有的顶点都被探索了。

    测试

    var deepPath = graph.DFS();
console.log(deepPath);
/**
发现了A
发现了B
发现了E
发现了I
探索了I
探索了E
发现了F
探索了F
探索了B
发现了C
发现了D
发现了G
探索了G
发现了H
探索了H
探索了D
探索了C
探索了A

discovery: [A: 1, B: 2, C: 10, D: 11, E: 3, F: 7, G: 12, H: 14, I: 4]
finished: [A: 18, B: 9, C: 17, D: 16, E: 6, F: 8, G: 13, H: 15, I: 5]
predecessors: [A: null, B: "A", C: "A", D: "C", E: "B", G: "D", H: "D", I: "E"]
*/

    小结

    本章学习了几种不同的方式来表示图这一数据结构。并实现了用邻接表表示图的算法。还学习了广度优先搜索和深度优先搜索的实际应用。

    书籍链接： 学习JavaScript数据结构与算法
  • 相关阅读:
    LeetCode "Jump Game"
    LeetCode "Pow(x,n)"
    LeetCode "Reverse Linked List II"
    LeetCode "Unique Binary Search Trees II"
    LeetCode "Combination Sum II"
    LeetCode "Divide Two Integers"
    LeetCode "First Missing Positive"
    LeetCode "Clone Graph"
    LeetCode "Decode Ways"
    LeetCode "Combinations"
  • 原文地址：https://www.cnblogs.com/lbh2018/p/JavaScript_Data_Structures_and_Algorithms_Part9.html
Copyright © 2011-2022 走看看