讲课人：
老师对dp的理解是类似于分治思想，由小状态推出大状态。不同的是分治算法没有重叠子问题。
dp把子问题越划越小，从而推出了基础状态。然后是dp方程，要满足简洁性，并且充分描述能够影响最后结果的条件。
转移？zhx：从小问题推到大问题就是转移。
思路：先把挂钩数量排个序
这个题和导弹拦截差不多，你对l进行从大到小排序，那么文题就变成了求最长不上升子序列的个数，也就是最长上升子序列的长度。
n^2做法。
先想n^4做法，然后一步一步优化。
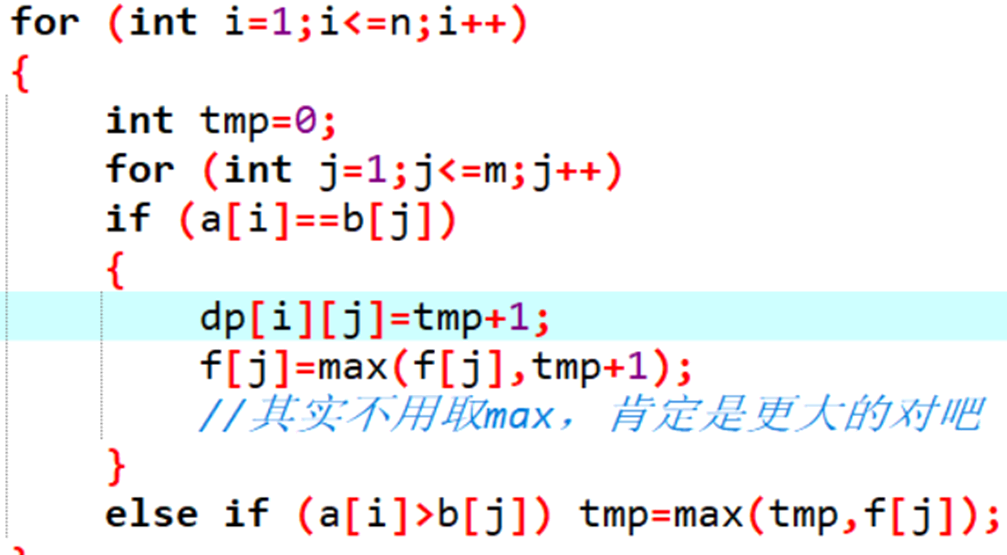
来道水题。
上午完结。
下午：
序列dp，区间dp
对于某个括号序列，把左右括号看成一组，对每个序列内部的括号进行消去操作，最后总能得到这样的东西：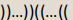
，于是我们可以吧这个题转化为另外一个题：
对于这个题，我们要为了不让血量低于0，按打怪物减少血量升序排列。
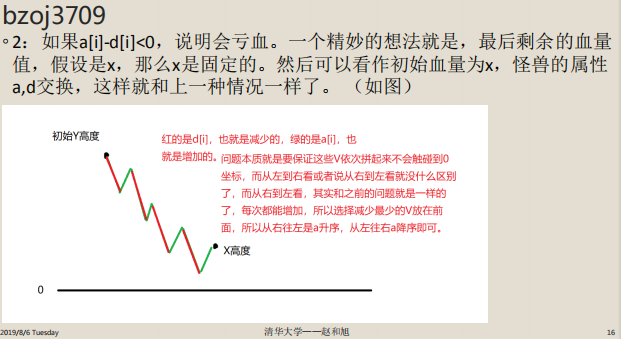
回到这个题：
这类问题：卡特兰数：
安利经典题：
代码如下：
区间dp：
转移方程：dp[i][j]=min(dp[i][k]+dp[k][j]+gcd(a[i],a[j]));很ez。
完结。zhx很强大