上午讲数位dp和背包问题。
先讲背包:


完全背包:换了个顺序:

多重背包:
多重背包优化:
这样把每个物品分成这些组,那么把他们转变成不同的物品,就变成了01背包问题;


滑动窗口取最值问题。单调队列优化。

方法很简单,枚举每一组中的其中一个物品计算即可。


小技巧:






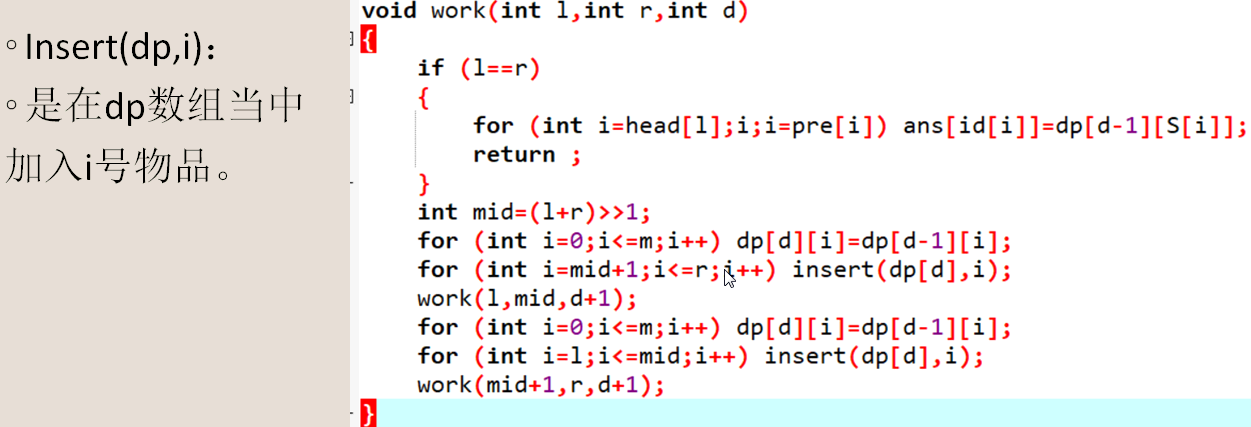


有些懵。。。

:

终于,到了数位dp环节:(恶心了一上午。)

dp方法:
判断上界。
假如我们要枚举到2147,当前已经枚举到了第二位,如果枚举到了1,那么我们说他达到了上界,下一位只能从0枚举到4。如果这一位是0,由于不管下一位是多少,这个数永远不可能大于原数,那么可以从0到9任意枚举。后几位也是如此。
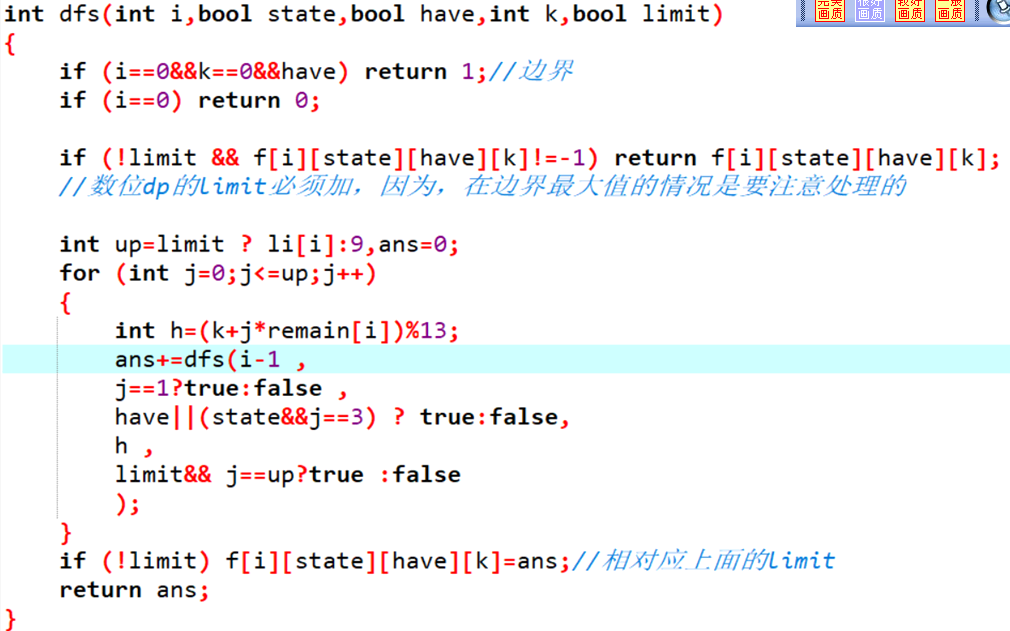
下午:




接着讲树形dp:
前言
1:与树或图的生成树相关的动态规划。
2:以每棵子树为子结构,在父亲节点合并,注意树具有天然的子结构。
这是很优美的很利于dp的。
3:巧妙利用Bfs或Dfs序,可以优化问题,或得到好的解决方法。
4:可以与树上的数据结构相结合。
5:树形Dp的时间复杂度要认真计算,部分问题可以均摊复杂度分析。
6:一般设f[u]表示u子树的最优价值或者是说方案数。
或者f[u][k]表示u子树附加信息为k的最优值,往往是通过考虑子树根节点
的情况进行转移。
第一题:








完结